python图表和对感知机的理解

1.画一个如下图的表格

import matplotlib.pyplot as plt
import numpy as np
y1 = np.linspace(-5,5,4)#每个柱形的y值，随机从（-5,5）中产生4个数字
x1=[0.5,2,3.5,5]#每个柱形左下角在X轴上的坐标
y2 = np.linspace(0,10,4)
x2=[1,2.5,4,5.5]
x3=[0.75,2.25,3.75,5.25]  #这个作为参照
rects1=plt.bar(x1,y1,width=0.5,label="1") 
rects2=plt.bar(x2,y2,width=0.5,label='2')
plt.xlabel("I'm X")
plt.ylabel("I'm Y")
plt.title("IT")
labels = ['One','Two','Three','Four']
plt.xticks(x3,labels)#以x3为参照
for rect in rects1:
    height = rect.get_height()
    plt.text(rect.get_x()+rect.get_width()/2, height, str(height), ha="center", va="bottom")
for rect in rects2:
    height = rect.get_height()
    plt.text(rect.get_x()+rect.get_width()/2, height, str(height), ha="center", va="bottom")
plt.legend()
plt.show()

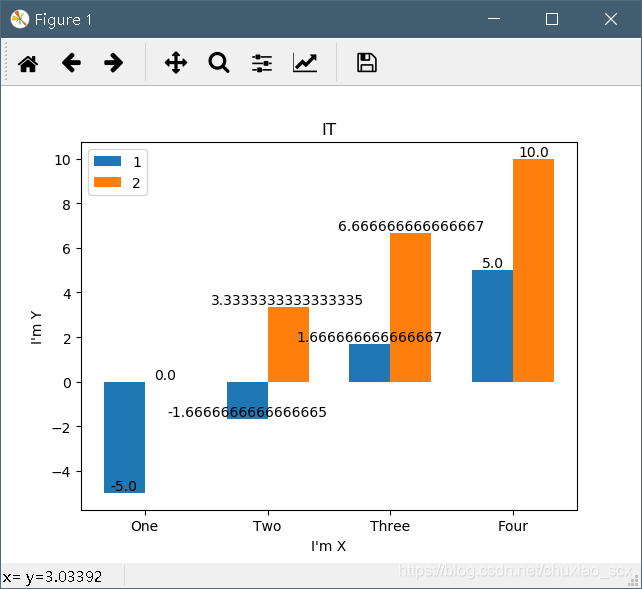不过这一看就是伪随机吧=-=。
2.根据我的理解，对下面的代码进行注释。

import numpy as np
import matplotlib.pyplot as plt

p_x = np.array([[3, 3], [4, 3], [1, 1], [2.5, 3]])# 输入四个点x1(3,3),x2(4,3),x3(1,1),x4(2.5,3)中x1,x2为正实例点，x3,x4为负实例点
y = np.array([1, 1, -1, -1])

# 绘制初始点
for i in range(len(p_x)):#循环，循环次数为p_x的行数，因为p_x有4行，所以循环4次
	if y[i] == 1:
		plt.plot(p_x[i][0], p_x[i][1], 'ro')#对面满足条件的点描红
	else:
		plt.plot(p_x[i][0], p_x[i][1], 'bo')#对不满足上个条件的点描蓝
		
# w超平面的法向量,b是超平面的截距，delta是指的是学习率
w = np.array([1, 0])
b = 0
delta = 1

for i in range(100):#循环，从i到100，每次循环i++；
	temp = -1
	for j in range(len(p_x)):#循环四次
		if y[j] != np.sign(np.dot(w, p_x[0]) + b): 	# dot函数表示向量点积
			temp = j
			break# 表示三个点都被正确分类
		if temp == -1:
			break
		w += delta * y[temp] * p_x[temp]
		b += delta * y[temp]

line_x = [0, 10]
line_y = [0, 0]

 # 超平面表达式为wx+b=0 其中w为向量 w1x1+w2x2+b=0 x2=(-w1x1-b)/w2
for i in range(len(line_x)):
	line_y[i] = (-w[0] * line_x[i] - b) / w[1]

plt.plot(line_x, line_y)
plt.grid(True)
plt.show()

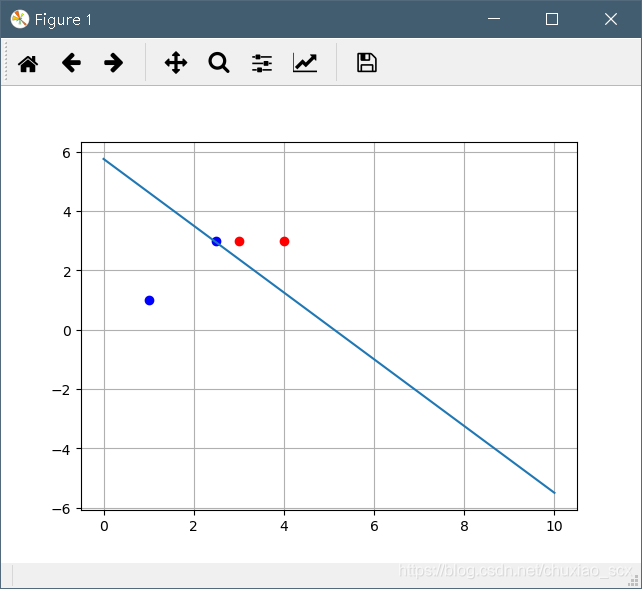
显而易见，这是个感知机的学习算法。

3.感知机的工作原理。

这里是引用https://blog.youkuaiyun.com/weixin_41648259/article/details/103002681
感知机（perceptron）是二类分类的线性分类模型，其输入时实例的特征向量，输出为实例的类别。取值为+1和-1。
感知机模型
定义：假设输入空间（特征空间）是Χ∈Rn(n维欧式空间）,输出空间是Y={1，-1}。输入x∈X表示实例的特征向量，对应于输入空间（特征空间）的点；输出y∈Y表示实例的类别。由输入空间到输出空间的映射如下：f(x)=sign(wx + b)称为感知机。其中w∈Rn叫做权值，b∈R(实数）表示偏置。
定义：假设输入空间（特征空间）是Χ∈Rn(n维欧式空间）,输出空间是Y={1，-1}。输入x∈X表示实例的特征向量，对应于输入空间（特征空间）的点；输出y∈Y表示实例的类别。由输入空间到输出空间的映射如下：f(x)=sign(wx + b)称为感知机。其中w∈Rn叫做权值，b∈R(实数）表示偏置。
感知机的学习策略
数据集
感知机训练的前提是训练集中的实例点都是线性可分的。
定义：给定一个数据集T={(x1,y1),(x2,y2),(x3,y3),……,(xn,yn)} 其中xi∈X=Rn (xi为向量不能理解为实数）yi∈Y={+1,-1}。
感知机训练的目的是找到一个能将训练集中的正实例点和负实例点完全分开的超平面。即确定感知机参数w,b的值。感知机所采用的学习策略是将经验损失极小化。将误分类点到超平面S的距离之和极小化。
Rn空间中x0点到超平面的距离：|wx0 + b |/||w|| （类比点到直线距离）。因此对于误分类点（xi,yi）来说-yi(w * xi+b)>0所以xi点到超平面的距离s为:-yi(w * xi + b)/||w||。
假设误分类点的集合为M,那么所有的误分类点到超平面s的总的距离为：
-1/||w||\sum yi(wxi+b)其中xi∈M。
感知机损失函数定义：
给定训练数据集T={(x1,y1),(x2,y2),(x3,y3),……,(xn,yn)}，xi∈X=Rn，yi∈Y={+1,-1}，i=1,2,3……，N 感知机sign(wx + b)损失函数定义为：L（w,b）= -\sum yi(wxi + b)(w,b)=-\sum yi(w * xi + b) 其中xi∈M。（说明1/||w||是常数，定义损失函数时不考虑）M是误分类点的集合，这个损失函数就是感知机学习的经验分险函数。显然如果没有误分类点，损失函数的数值是0，误分类点越少，误分类函数的值就越小。损失函数L（w,b）= -\sum yi(wxi + b)(w,b)是连续可导函数。
感知机学习算法
感知机学习的目是求参数w,b使其为以下损失函数极小化问题的解：minL(w,b)=-\sum yi(wxi + b) 其中xi∈M，并且损失函数时关于w,b的函数。在极小化的过程中不是一次使用M中所有的误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。损失函数的梯度：由▽wL(w,b)=-\sum yixi，▽bL(w,b)=-\sum yi 给出：w ←w+ηyixi ,b←b+ηyi 其中η是学习率。

看懂了吗？我也不太懂。
个人的理解是给定初始的数据，然后电脑会自动根据其数据求出相应的函数，这个函数是线性的。然后每次电脑都会根据设定的学习率自动下调或上涨斜率来使得这个线性关系更加接近真实的关系。这个真实关系由初始输入的数据来定义。
比如四个点，两个点为1（表示真实），两个点为-1（表示虚假）。感知机所求的方程就是将这些点完全分开，真实的为一边，虚假的为一边。