第14期（六月）组队学习 Task3：Haar特征描述算子-人脸检测

Haar特征描述算子-人脸检测

Haar特征是用于物体识别的一种数字图像特征，与哈尔小波转换极为相似，也是第一种即时的人脸检测运算；同时是一种用于目标检测或识别的图像特征描述子，通常和AdaBoost分类器组合使用，Haar特征对AdaBoost训练出的强分类器进行级联，使其成为人脸检测以及识别领域较为经典的算法。

1 Haar特征简介

Haar特征分为三类：边缘特征、线性特征、中心特征和对角线特征，组合成特征模板。特征模板内有白色和黑色两种矩形，并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。Haar特征值反映了图像的灰度变化情况。例如：脸部的一些特征能由矩形特征简单的描述，如：眼睛要比脸颊颜色要深，鼻 梁两侧比鼻梁颜色要深，嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构，如边缘、线段较敏感，所以只能描述特定走向（水平、垂直、对角）的结构，如下图所示。

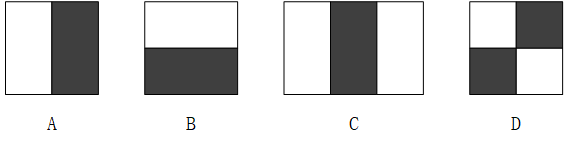
对于图中的$A$, $B$和$D$这类特征，特征数值计算公式为：$v=\Sigma 白-\Sigma 黑$，而对于$C$来说，计算公式为：$v=\Sigma 白-2\ast \Sigma 黑$；将黑色区域像素和乘以2，是为了使两种矩形区域中像素数目一致。即白色区域的权值为正值，黑色区域的权值为负值，而且权值与矩形区域的面积成反比，可以抵消两种矩形区域面积不等造成的影响，保证Haar特征值在灰度分布均匀的区域特征值趋近于0。

通过改变特征模板的大小和位置，可在图像子窗口中穷举出大量的特征。上图的特征模板称为“特征原型”；特征原型在图像子窗口中扩展（平移伸缩）得到的特征称为“矩形特征”；矩形特征的值称为“特征值”。

矩形特征可位于图像任意位置，大小也可以任意改变，所以矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化，使得 很小的检测窗口含有非常多的矩形特征，如：在24*24像素大小的检测窗口内矩形特征数量可以达到16万个。需要解决两个问题：（1）快速计算Haar矩形特征值？—积分图；（2）筛选有效的矩形特征用于分类识别？—可以通过AdaBoost算法来训练。

1.1 积分图

1.1.1 积分图构建

在一个图像窗口中，可以提取出大量的Haar矩形特征区域，如果在计算Haar特征值时，每次都遍历矩形特征区域，将会造成大量重复计算，严重浪费时间。积分图是一种快速计算矩形特征的方法，主要思想是将图像起始像素点到每一个像素点之间所形成的矩形区域的像素值的和，作为一个元素保存下来，即将原始图像转换为积分图(或者求和图)，当求某一矩形区域的像素和时，只需要索引矩形区域4个角点在积分图中的取值，进行普通的加减运算，即可求得Haar特征值，整个过程只需遍历一次图像，计算特征的时间复杂度为常数$(O(1))$，可以大大提升计算效率。
积分图中元素的公式定义如下：
$$ii(x,y)={\Sigma }_{k\le x,l\le y}f(k,l)$$
上式含义是在$(x,y)$(第$x$行第$y$列)位置处，积分图中元素为原图像中对应像素左上角所有像素值之和，$ii(x,y)$表示一个积分图像。在具体实现时，可用下式进行迭代运算。
$$s(x,y)=s(x,y-1)+i(x,y)$$
$$ii(x,y)=ii(x-1,y)+s(x,y)$$
$s(x,y)$为行方向的累加值，初始值$s(x,-1)=0,ii(-1,y)=0$

1.1.2 计算Haar特征值

构建好积分图后，图像中任何矩形区域的像素值累加和都可以通过简单的加减运算快速得到，如下图所示，矩形区域D的像素和值计算公式如下：
$$Sum(D)=ii(x_4,y_4)-ii(x_2,y_2)-ii(x_3,y_3)+ii(x_1,y_1)$$

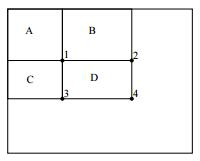
矩形区域求和示意图
在下图中，以水平向右为x轴正方向，垂直向下为y轴正方向，可定义积分图公式Summed Area Table($SAT(x,y)$)
$$SAT(x,y)={\Sigma }_{x’\le x,y’\le y}i(x’,y’)$$
以及迭代求解式
$$SAT(x,y)=SAT(x,$$