到现在建图还是不熟练，请看这篇（C++）

一.什么是图

首先，我们要了解什么是图（知道可以跳过）

图就是图。

首先，图由两部分组成：

1.结点

2.边

给一个图就知道了：

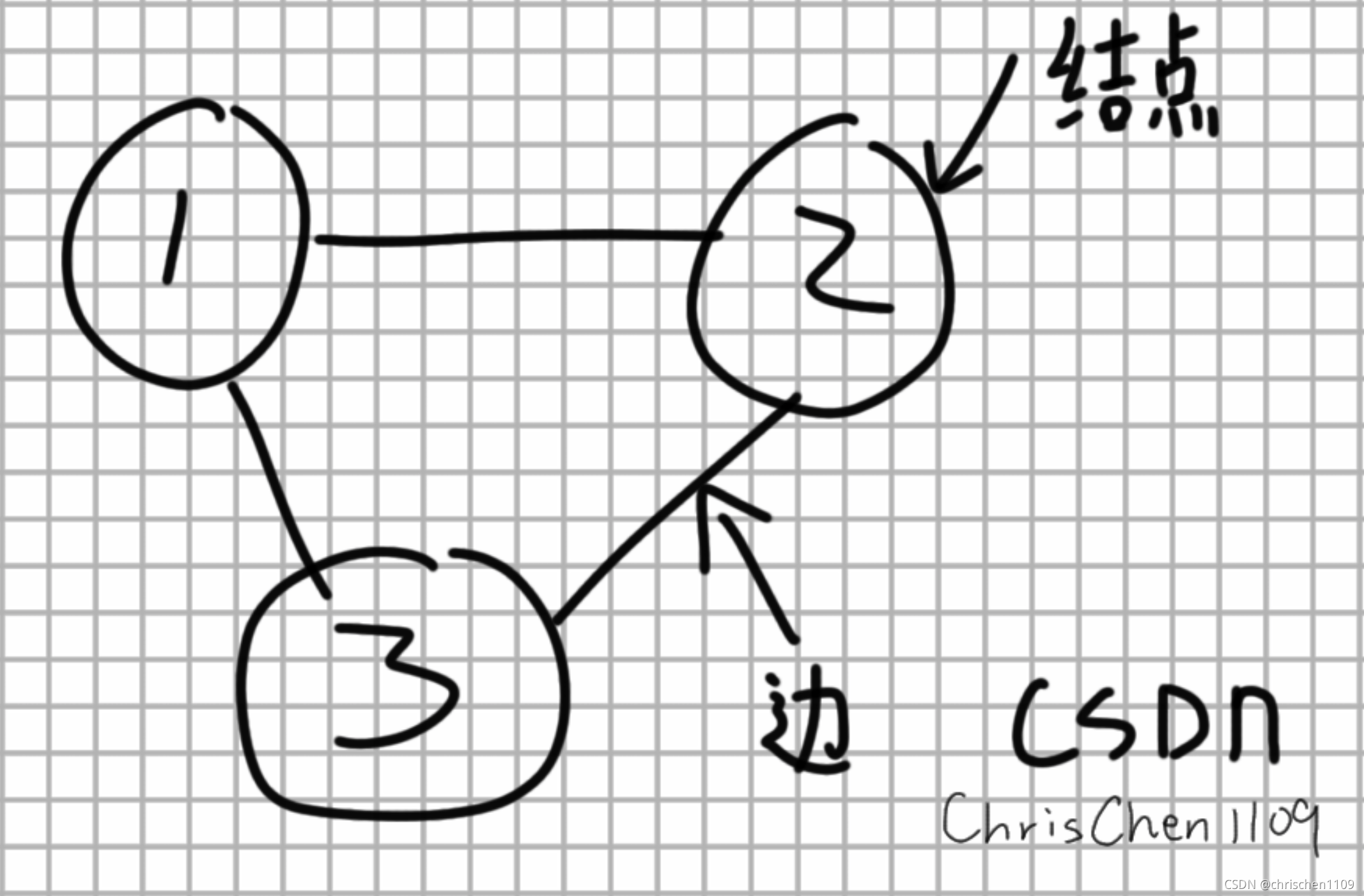
其次，图大致分为两种：

1.有向图：就是边是有方向的

  

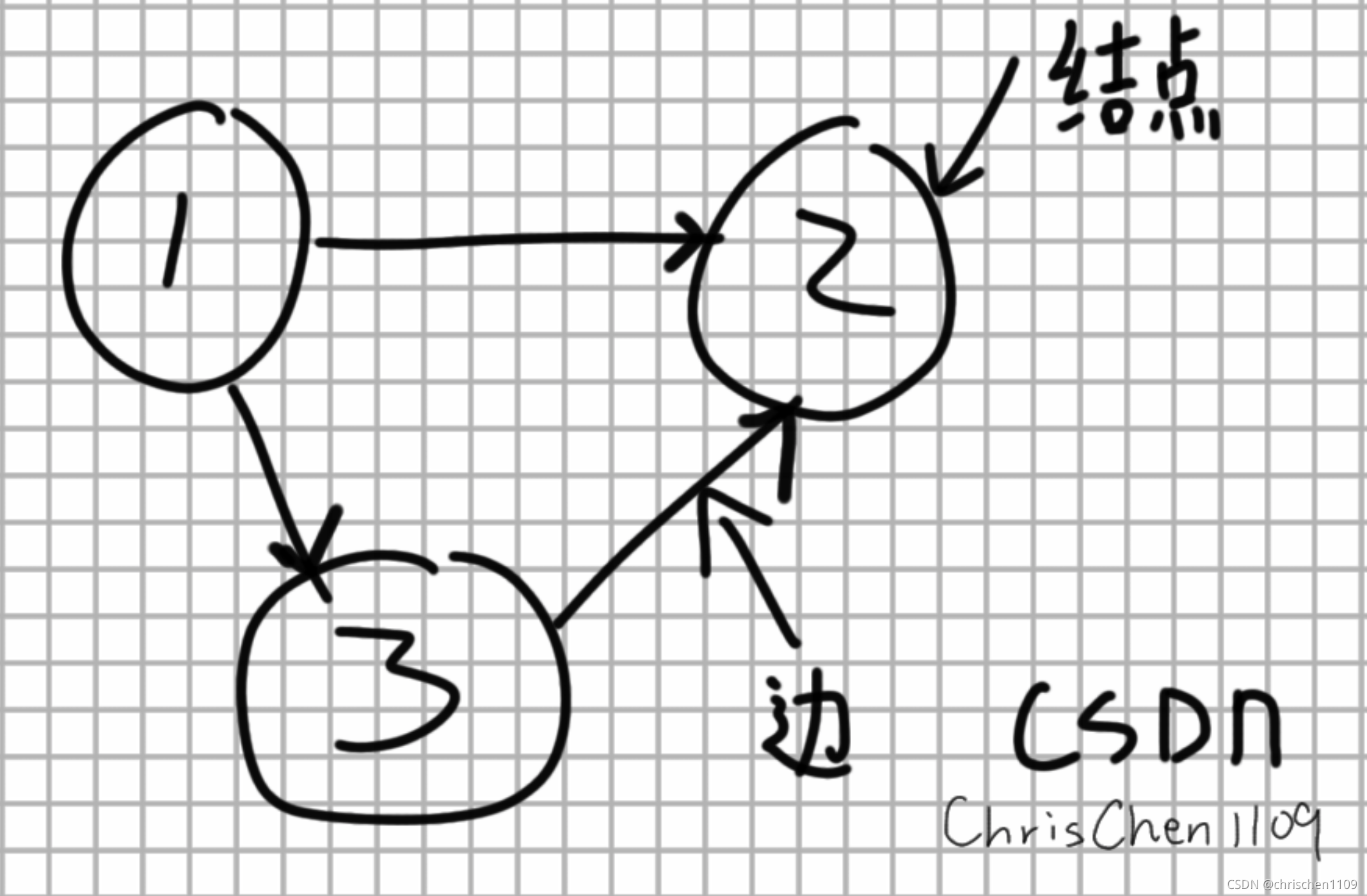
2.无向图：就是边是无方向的

 再其次，结点有三个属性：

1.入度：就是指向这个结点的边的数量

2.出度：就是指从这个结点出发指向别的结点的边的数量

3.权值：就是这个结点的值（不是编号）

（无向图中所有结点的入度都等于出度）

（同时，边也有可能有权值属性）

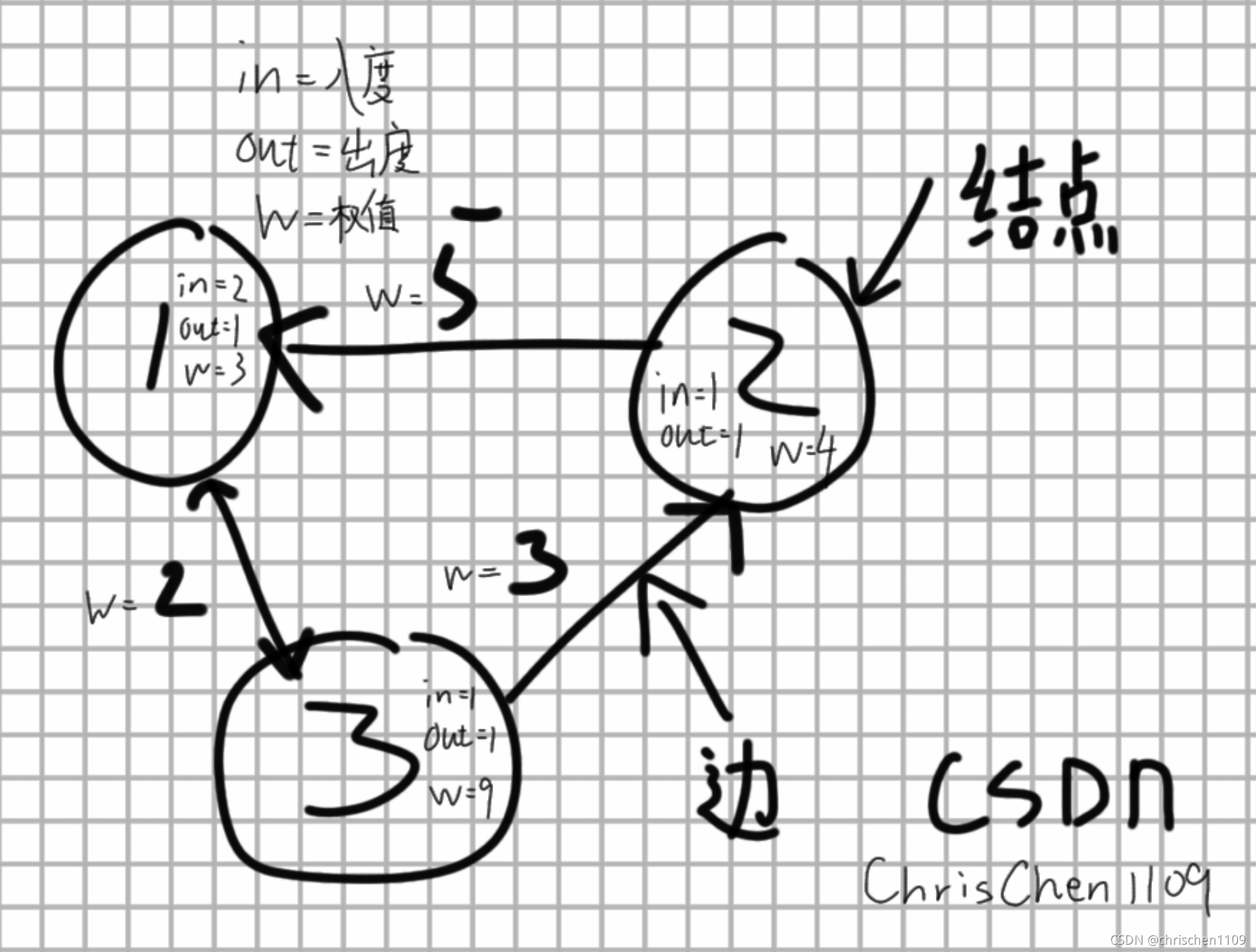
 （刚开始用手写板，请谅解字不好看的问题）

最后，在知道了这些后，我们图的类型有多了起来：

1.简单图：不存在自身指向自身的边，不存在两条重复的边

下面的图就不是简单图：

2.完全无向图：无向图，同时任意两个点之间都有边相连

 

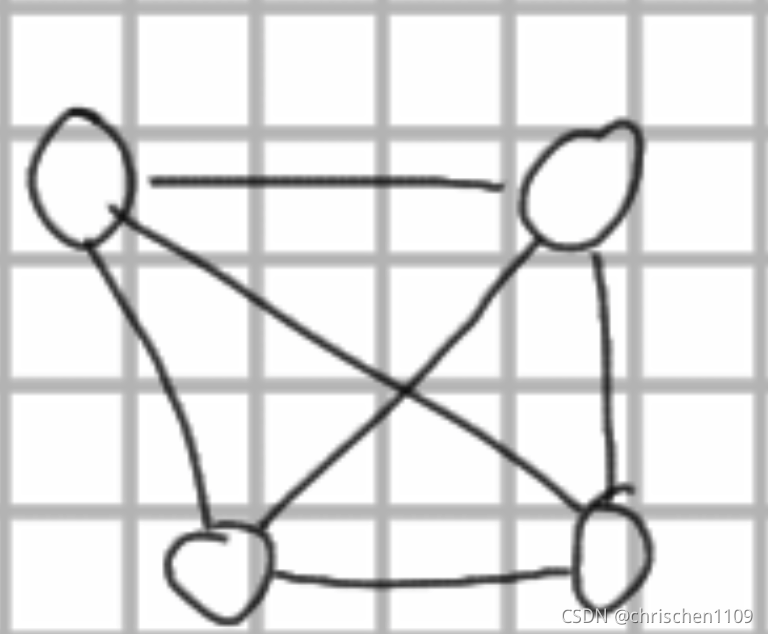
3.完全有向图：有向图，同时任意两个点之间都有互相指向的边。

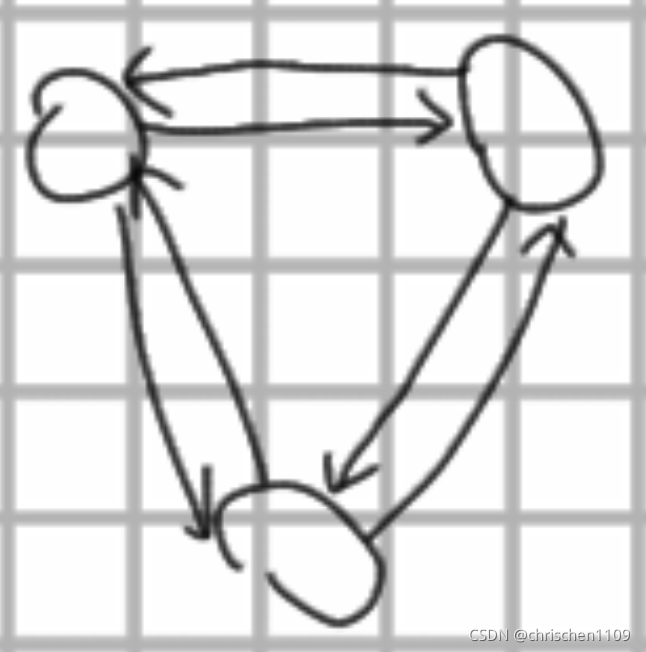
之后，你们还会学到各种各样的图，不在此赘述了。

二.怎么建图

首先，建图一般有两种思路：

1.邻接矩阵

2.邻接表

我们一个个来说。

邻接矩阵

首先说一下大体思路：

用数组来存储点与点的关系：

一开始吧所有点的距离都设置为INF(无穷大)就是无法到达的意思。

然后没读入一条权值为w边连接两个结点x、y就吧G[x][y]设为w。

最后，如果G[i][j]不等于INF就表示i和j两个点有边相连，并且条边的权值为G[i][j]。

示意图：

 

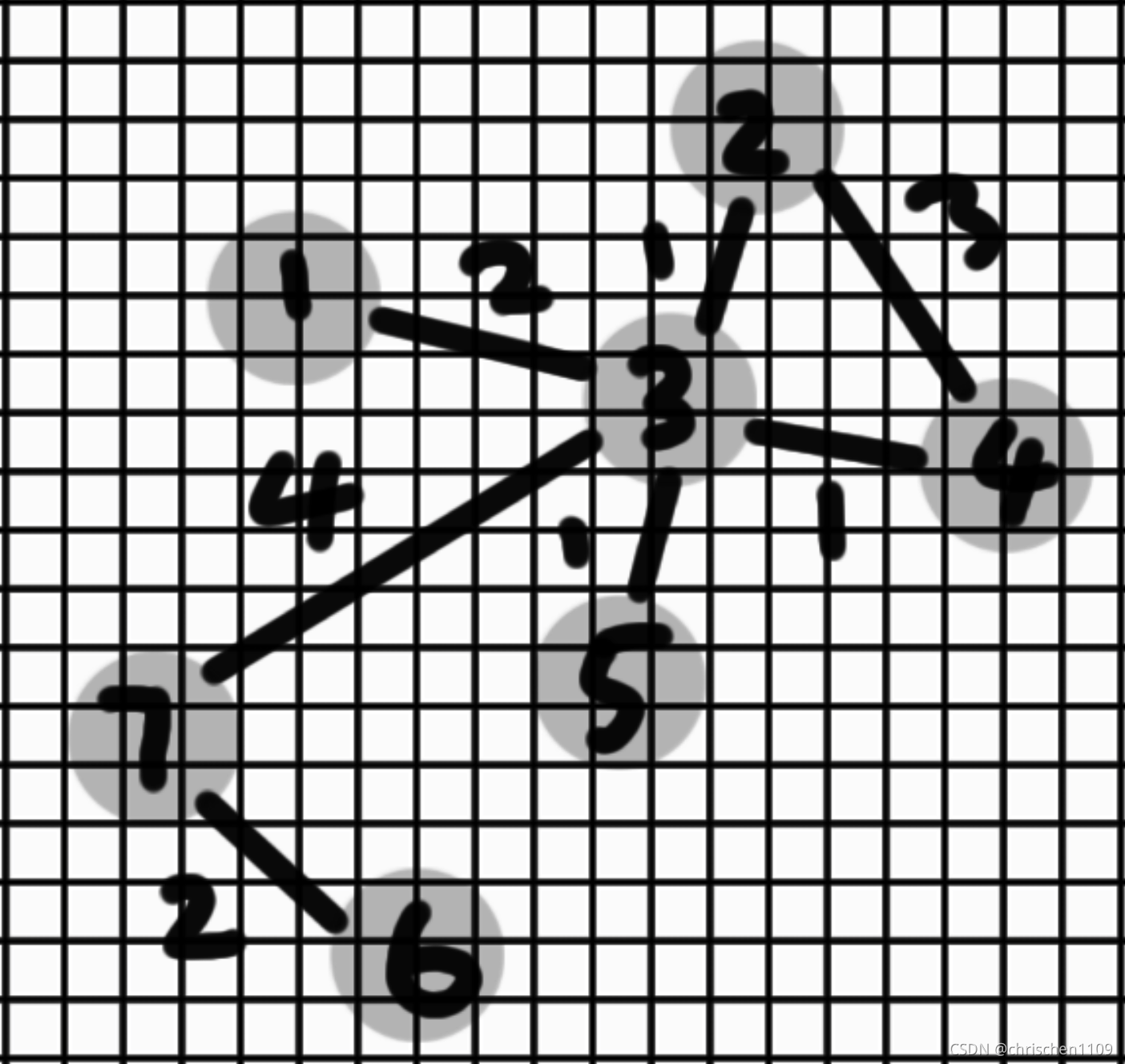
就可以表示成：

 代码：
 

#include <iostream>
#include <iomanip>

using namespace std;

const int N = 1010;
const int inf = 2147483647; // int最大值

int g[N][N]; // 邻接矩阵
int n; // 点的数量
int m; // 边的数量

void init() // 初始化邻接矩阵
{
    for (int i = 0; i < 1010; i ++ )
    {
        for (int j = 0; j < 1010; j ++ )
        {
            if (i == j) // 自己到自己的距离永远为0
                g[i][j] = 0;
            else  // 两个不同点之间一开始距离为无穷大（无法到达）
                g[i][j] = inf;
        }
    }
}

int main()
{
    init();
    
    cin >> n >> m;
    
    for (int i = 1; i <= m; i ++ )
    {
        int x, y, w;
        
        cin >> x >> y >> w;

        // 有向图：
        // g[x][y] = w;
        
        // 无向图要互相指向：
        g[x][y] = w;
        g[y][x] = w;
    }

    // 格式化输出
    cout << ' ';
    for (int i = 1; i <= n; i ++ )
        cout << setw(5) << i;
    cout << endl;
    
    for (int i = 1; i <= n; i ++ )
    {
        cout << i << ' ';
        for (int j = 1; j <= n; j ++ )
        {
            if (g[i][j] == inf)
                cout << setw(5) << "inf";
            else
                cout << setw(5) << g[i][j];
        }
        cout << endl;
    }
    
    return 0; // 完美结束=)
}

邻接表

同样，先讲一下思路： 

实际上邻接表和邻接矩阵差不多，只是这样更节省存储空间。

就使用一个Vector数组来存储所有与v[i]相连的点的信息。

同时，因为Vector是动态的，所以可以节省很多的存储空间。

（不知道什么是Vector的同学可以去看一下我的STL详解：）

实际上邻接表一共有两种方式（名字是我发明的）：

1.全邻接表

2.半邻接表

全邻接表

首先图解一下思路：

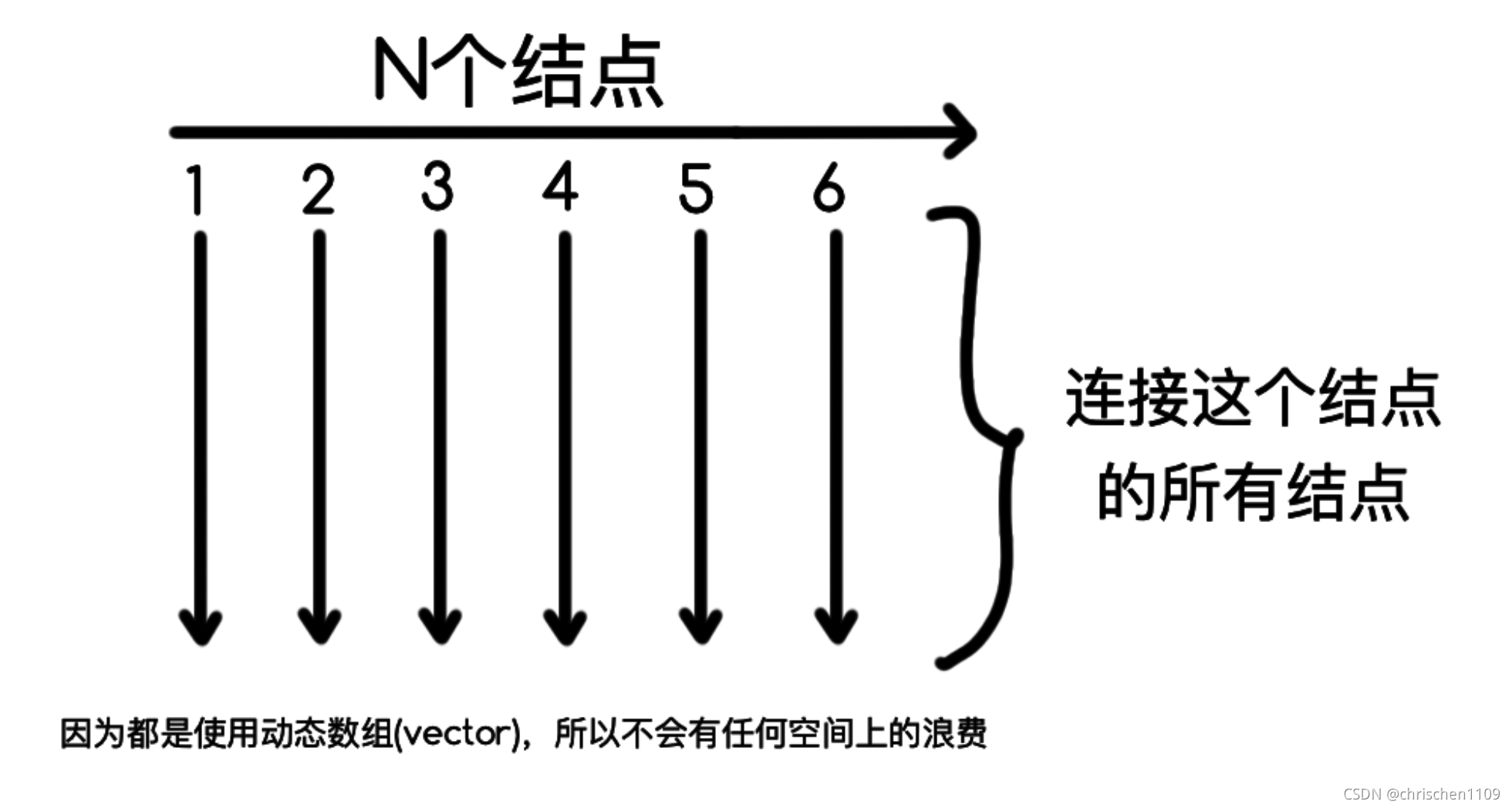
实际上就是Vector套Vector

#include <iostream>
#include <vector>

using namespace std;

struct node // 每一个点的结构体，方便存储
{
    int y; // 连接的点
    int w; // 边的权值
};

vector<vector<node>> g;
int n, m;

int main()
{
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++ )
    {
        vector<node> empty;
        g.push_back(empty); // 建立n个点的表，方便存储
    }
    
    for (int i = 1; i <= m; i ++ )
    {
        int x, y, w;
        
        cin >> x >> y >> w;

        //有向图
        //g[x].push_back({y, w});
        
        //无向图，需要双向建边
        g[x].push_back({y, w});
        g[y].push_back({x, w});
    }

    //格式化输出    
    for (int i = 1; i <= n; i ++ )
    {
        cout << i << ":";
        for (int j = 0; j < g[i].size() - 1; j ++ )
            cout << g[i][j].y << "(w=" << g[i][j].w << ')' << ',';
        cout << g[i][g[i].size() - 1].y << "(w=" << g[i][g[i].size() - 1].w << ')' << endl;
    }
    
    return 0;
}

图：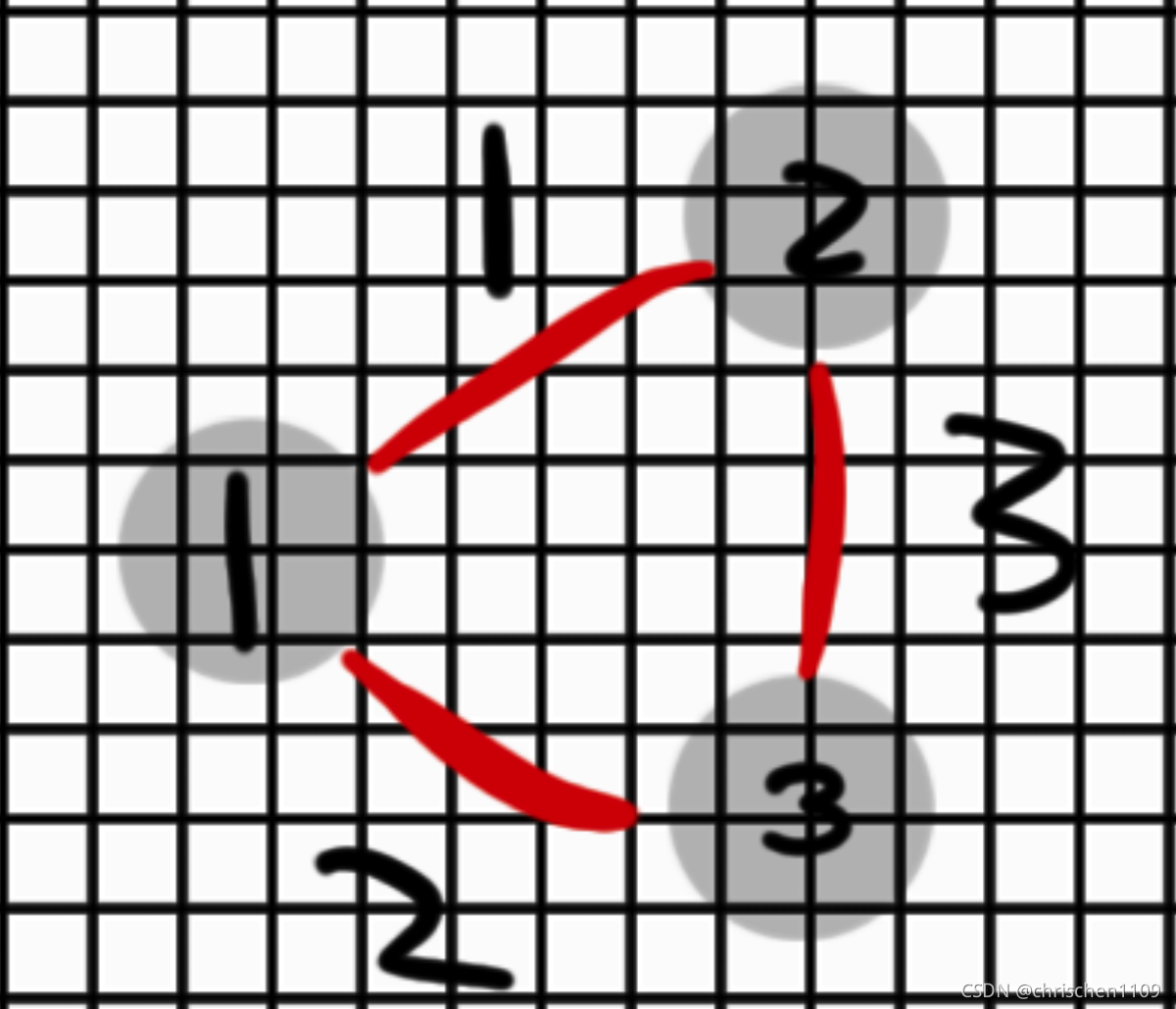

建图后的数据：

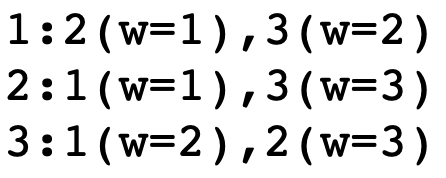
半邻接表 

半邻接表实际上就是降级版的全邻接表，也是比较常用一种邻接表

降级的地方：只有连接的结点是用动态数组存储，而所有结点依旧采用数组存储

（这里就不图解了，自己脑补吧（因为作者懒）） 

代码：

#include <iostream>
#include <vector>

using namespace std;

const int N = 1e5 + 10; // 点的个数的上线

struct node
{
    int y;
    int w;
};

vector<node> g[N];
int n, m;

int main()
{
    cin >> n >> m;
    
    for (int i = 1; i <= m; i ++ )
    {
        int x, y, w;
        
        cin >> x >> y >> w;

        // 有向图
        // g[x].push_back({y, w});

        // 无向图
        g[x].push_back({y, w});
        g[y].push_back({x, w});
    }
    
    for (int i = 1; i <= n; i ++ )
    {
        cout << i << ':';   
        for (int j = 0; j < g[i].size() - 1; j ++ )
        {
            cout << g[i][j].w << '(' << g[i][j].y << ')' << ',';
        }
        cout << g[i][g[i].size() - 1].w << '(' << g[i][g[i].size() - 1].y << ')' << endl;
    }
    
    return 0; // =)
}

SO， 如果这篇博客对你有帮助，请给我一个赞吧，这是对我最大的帮助（谢谢🙏）。