/**
* 快速排序:
* 找两个哨兵,一个从头i,一个从尾j
* 设置一个基准tmp
* i和j与tmp比较,
* 如果i<tmp,i++
* 如果i>tmp,i和j交换位置
* 再比较的话就变成
* 如果j>tmp,j--
* 如果j<tmp,i和j交换位置又变成之前的状态
* 一直到i,j相遇,排序完毕,把tmp放在他们相遇的位置
* 再递归,两边再次用这种方法
*
* 空间复杂度:
* 需要用堆栈来实现递归,
* 如果每次都平均分成两半,空间复杂度是logn
* 如果每次都是一个,最坏的情况,倒序,空间复杂度是n
* 平均空间复杂度是O(logn)
* 时间复杂度:
* 时间效率依赖划分是否平衡
* 最坏的情况,倒序,每次划分都有一个空的子序列,
* 内循环次数就和外循环一样,时间复杂度是O(n2)
* 最好的情况:每次都分成平均的两部分,
* 这样内循环就是外循环的logn次,时间复杂度是ologn
* 平均时间复杂度nlogn
*
* 经实验证明,在所有同数量级的情况下,快排的平均性能最好。
* 被认为最好的一种排序方法,但是当序列基本有序,快排就要退化成冒泡。
* 时间复杂度变成了n2。
* 解决办法:采取随机选择基准(tmp)的方法。可以改进排序前基本有序的性能。
* @param arr
*/
public static void kuaisuSort(int[] arr) {
// ks(arr, 0, arr.length - 1);
ksPro(arr, 0, arr.length - 1);
}
public static void ks(int[] arr, int f, int l) {
if (f < l) {
int mid = ksSort(arr, f, l);
ks(arr, f, mid - 1);
ks(arr, mid + 1, l);
}
}
public static int ksSort(int[] arr, int first, int last) {
int tmp = arr[first];
while (first < last) {
while (first < last && arr[last] >= tmp) {
last--;
}
arr[first] = arr[last];
while (first < last && arr[first] <= tmp) {
first++;
}
arr[last] = arr[first];
}
arr[first] = tmp;
return first;
// ksSort(arr, f, first-1);
// ksSort(arr, first+1, l);
}
public static void ksPro(int[] arr, int f, int l) {
if (f < l) {
// 选取数组中随机的一个元素和第一个元素进行交换,这样基准就变成了随机的元素
swap(arr, f, new Random().nextInt(l - f + 1)+f);
int mid = ksSort(arr, f, l);
ksPro(arr, f, mid - 1);
ksPro(arr, mid + 1, l);
}
}
public static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
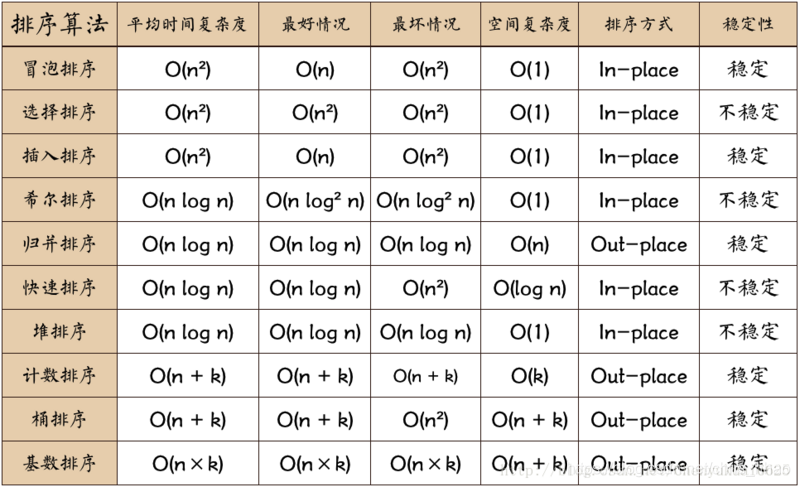






 本文深入探讨了快速排序算法的工作原理,包括其分治策略、枢轴元素的选择以及递归过程。通过实例展示了如何实现快速排序,并分析了其平均及最坏情况下的时间复杂度,揭示了它作为高效排序算法的优势。
本文深入探讨了快速排序算法的工作原理,包括其分治策略、枢轴元素的选择以及递归过程。通过实例展示了如何实现快速排序,并分析了其平均及最坏情况下的时间复杂度,揭示了它作为高效排序算法的优势。
















 3077
3077

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








