选择排序法

最新推荐文章于 2025-09-13 00:00:00 发布

原创最新推荐文章于 2025-09-13 00:00:00 发布 · 263 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构 #排序算法

程序设计（算法与数据结构篇）专栏收录该内容

30 篇文章

订阅专栏

本文深入解析了插入排序算法，包括其工作原理、伪代码实现、C++代码实例以及时间复杂度和稳定性分析。通过详细的步骤说明，读者可以了解到插入排序如何在每个计算步骤中找出最小值并完成排序，同时理解其在不同数据序列下的表现。

选择排序

一选择排序了解

选择排序法是一种非常直观的算法，他会在每个计算步骤中选出一个最小值，进而完成排序
流程图：
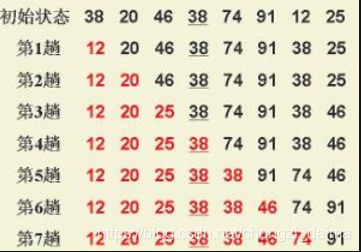
在这里插入图片描述

二选择排序伪代码实现

insertionSort(A,N)//包含N个元素的0起点数组A
{
	for i 从 1到 N-1 
	{
	   V = A[i]
	   j=i-1
	   while(j>=0 且 A[j]>v)
	   {
	       A[j+1]=A[j]
	       j--;
	   }
	   A[j+1]=v
	}
}

三选择排序 c++ 代码实现

插入排序法所需的主要变量：

A[N]	长度为N的整型数组
i	循环变量，表示未排序部分的开头元素，初始值为1
v	临时保存 A[ i ] 值的变量
j	循环变量，用于在已排序部分寻找v的插入位置

代码如下：

void InsertionSort(vector<int> &ivec)
{
	if(ivec.size()==0) return;
	for (decltype(ivec.size()) i = 1; i !=ivec.size() ; ++i) {
          auto v=ivec.at(i);
          j=i-1;
          while(j>=0 && ivec.at(j)>v)   //寻找插入位置的过程
		  {
          	  ivec.at(j+1)=ivec.at(j);   //需要将插入位置之后的元素向后移动
          	  --j;                       
		  }
          ivec.at(j+1)=v;                //找到插入位置
	}
}