排序算法总结

最新推荐文章于 2024-10-22 17:17:53 发布

chokshen

最新推荐文章于 2024-10-22 17:17:53 发布

阅读量280

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构和算法

本文链接：https://blog.youkuaiyun.com/chokshen/article/details/68951360

数据结构和算法专栏收录该内容

4 篇文章

订阅专栏

本文详细介绍了基本排序算法（如冒泡排序、简单选择排序、插入排序）及优化的排序算法（如希尔排序、堆排序、归并排序、快速排序）的实现原理及C语言和Java语言的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这段时间学习了排序算法，然后根据自己的思路敲了一遍代码，排序算法大概分为两种：基本排序算法，比如说冒泡排序，简单选择排序，插入排序；优化的排序算法，比如说希尔排序，堆排序，归并排序和快速排序等。

以下是算法实现需要的头文件和公用函数（数组都是从0开始）：

#include <stdio.h>
#include "stdlib.h"
void swap (int a[],int i,int j) {
    int temp=a[i];
    a[i]=a[j];
    a[j]=temp;
}

1.冒泡排序

void BubbleSort (int a[],int n) {
    for (int i=0; i<n; i++) {
        for (int j=n-1; j>i; j--) {
            if (a[j]<a[j-1]) {
                swap(a, j, j-1);
            }
        }
    }
}

2.简单交换排序

void SelectSort (int a[],int n) {
    for (int i=0; i<n; i++) {
        int min=i;
        for (int j=i+1; j<n; j++) {
            if (a[j]<a[min]) {
                min=j;
            }
        }
        if (min!=i) {
            swap(a, i, min);
        }
    }
}

3.插入排序

void InsertSort (int a[],int n) {
    int i,j,temp;
    for (i=1; i<n; i++) {
        if (a[i]<a[i-1]) {  //每完成一次插入，a[j-1]都是最大值
            temp=a[i];
            for (j=i-1; j>=0 && a[j]>temp; j--) {
                a[j+1]=a[j];
            }
        }
        a[j+1]=temp;
    }
}

4.希尔排序

void ShellSort (int a[],int n) {
    int i,j,temp;
    int step=n;
    do {
        step=step/3+1; //步长
        for (i=step; i<n; i++) {
            if (a[i]<a[i-step]) {
                temp=a[i];
                for (j=i-step;j>=0 && a[j]>temp ; j-=step) {
                    a[j+step]=a[j];
                }
                a[j+step]=temp;
            }
        }
    } while (step>1);
}

5.堆排序

//堆排序(大顶堆)
////堆调整,在i+1节点至m节点已经为大顶堆的基础上，将i结点至m结点调整为大顶堆。由于数组从0开始计算，i节点的子结点为2*i+1, 2*i+2，总结点数为m+1。
void HeapAdjust (int a[],int i,int m) {
    int j,temp;
    temp=a[i];
    for (j=2*i+1; j<m+1; j=2*j+1) {   //m+1为结点总数
        if (j+1<m+1 && a[j]<a[j+1]) {  //左右孩子结点必须要小于总结点数
            j++;
        }
        if (temp>=a[j]) {
            break;
        } else {
            a[i]=a[j];
            i=j;
        }
    }
    a[i]=temp;
}

void HeapSort (int a[],int n) {
    int i;
    //建堆
    for (i=n/2-1; i>=0; i--) { //  初始值i=(n-1-1)/2,i=0为根结点
        HeapAdjust(a,i,n-1);
    }
    
    for (i=n-1; i>0; i--) {
        swap(a, 0, i);  //交换后根结点以下（除去最后一个结点）任然是大顶堆
        HeapAdjust(a, 0, i-1);
    }
}

6.归并排序

C语言：

//将二个有序数列a[first...mid]和a[mid+1...last]合并
void Merge (int a[],int temp[],int first,int last ,int mid) {
    int i=first,j=mid+1;;
    int m=mid,n=last;
    int k=0;
    while (i<=m && j<=n) {
        if (a[i]<a[j]) {
            temp[k++]=a[i++];
        }else {
            temp[k++]=a[j++];
        }
    }
    while (i<=m) {
        temp[k++]=a[i++];
    }
    while (j<=n) {
        temp[k++]=a[j++];
    }
    
    for (int t=0; t<k; t++) {
        a[first+t]=temp[t];
    }
}

//归并排序递归
void MSort (int a[],int temp[],int first,int last ) {
    int mid;
    if (first<last) {
        mid=first+(last-first)/2;
        MSort(a, temp, first, mid);   //左边有序
        MSort(a, temp, mid+1, last);  //右边有序
        Merge(a, temp, first, last, mid); //将两个有序序列合并
    }
}

//归并排序
void MergeSort (int a[],int n) {
    int *temp=malloc(n*sizeof(int));
    MSort(a, temp, 0, n-1);
    free(temp);
}

Java：

    public void MergeSort(int[] nums) {
        int[] temp = new int[nums.length];
        MSort(nums, temp, 0, nums.length - 1);
    }

    private void MSort(int[] nums, int[] temp, int low, int high) {
        if(low < high) {
            int mid = low + (high - low) / 2;
            MSort(nums, temp, low, mid);
            MSort(nums, temp, mid + 1, high);
            Merge(nums, temp, low, mid, high);
        }
    }

    private void Merge(int[] nums, int[] temp, int low, int mid, int high) {
        int i = low;
        int j = mid + 1;
        int k = 0;
        while(i <= mid && j <= high) {
            if(nums[i] < nums[j]) {
                temp[k++] = nums[i++];
            } else {
                temp[k++] = nums[j++];
            }
        }
        while(i <= mid) {
            temp[k++] = nums[i++];
        }
        while (j <= high) {
            temp[k++] = nums[j++];
        }
        for(int m = 0; m < k; m++) {
            nums[low + m] = temp[m];
        }
    }

7.快速排序

（1）单轴

C语言：

//快速排序分割函数
int Partition (int a[],int low,int high) {
    int pivot=a[low];
    while (low<high) {
        while (low<high && a[high]>=pivot) {
            high--;
        }
        swap(a, low, high);
        while (low <high && a[low]<=pivot) {
            low++;
        }
        swap(a, low, high);
    }
    pivot=low;
    return pivot;
}

//快速排序递归
void QSort (int a[],int low,int high) {
    if (low<high) {
        int pivot=Partition(a, low, high);
        QSort(a, low, pivot-1); //低子表递归排序
        QSort(a, pivot+1, high);//高子表递归排序
    }
}

//快速排序
void QuickSort (int a[],int n) {
    QSort(a, 0, n-1);
}

Java：

    public void QuickSort(int[] nums) {
        QSort(nums, 0, nums.length - 1);
    }

    private void QSort(int[] nums, int low, int high) {
        if(low < high) {
            int pivot = Partition(nums, low, high);
            QSort(nums, low, pivot - 1);
            QSort(nums, pivot + 1, high);
        }
    }

    private int Partition(int[] nums, int low, int high) {
        int pivot = nums[low];
        while(low < high) {
            while(low < high && nums[high] >= pivot) {
                high--;
            }
            swap(nums, low, high);
            while(low < high && nums[low] <= pivot) {
                low++;
            }
            swap(nums, low, high);
        }
        return low;
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }

（2）三向切分

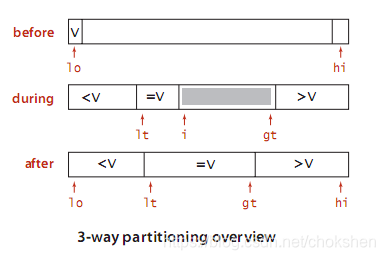
算法思想：对于每次切分：从数组的左边到右边遍历一次，维护三个指针，其中lt指针使得元素（arr[0]-arr[lt-1]）的值均小于切分元素；gt指针使得元素（arr[gt+1]-arr[N-1]）的值均大于切分元素；i指针使得元素（arr[lt]-arr[i-1]）的值均等于切分元素，（arr[i]-arr[gt]）的元素还没被扫描，切分算法执行到i>gt为止。每次切分之后，位于gt指针和lt指针之间的元素的位置都已经被排定，不需要再去处理了。之后将（lo,lt-1）,（gt+1,hi）分别作为处理左子数组和右子数组的递归函数的参数传入，递归结束，整个算法也就结束。

C语言：

//快速排序递归
void QSort (int a[],int lo,int hi) {
     if(lo>=hi) return;  //单个元素或者没有元素的情况
     //循环不变量定义
     // all in [lo, lt) < pivot
     // all in [lt, i) = pivot
     // all in (gt, hi] > pivot
     int lt=lo;
     int i=lo+1;  //第一个元素是切分元素，所以指针i可以从lo+1开始
     int gt=hi;
     int v=a[lo];
     while(i<=gt)
     {
         if(a[i]<v)  //小于切分元素的放在lt左边，因此指针lt和指针i整体右移
             swap(a,lt++,i++ );  
         else if (a[i]>v)  //大于切分元素的放在gt右边，因此指针gt需要左移
             swap(a,i,gt-- );
         else
             i++;
     }
     QSort(a, lo, lt-1); //低子表递归排序
     QSort(a, gt+1, high);//高子表递归排序
}

//快速排序
void QuickSort (int a[],int n) {
    QSort(a, 0, n-1);
}

Java：

    public void QuickSort(int[] nums) {
        QSort(nums, 0, nums.length - 1);
    }

    private void QSort(int[] nums, int low, int high) {
        if(low >= high) {
            return;
        }
        //循环不变量定义
        //[lo, lt)小于
        //[lt, i)等于
        //(gt, hi]大于
        int target = nums[low];
        int lt = low;
        int i = lt + 1;
        int gt = high;
        while(i <= gt) {
            if(nums[i] < target) {
                swap(nums, lt++, i++);
            } else if(nums[i] > target) {
                swap(nums, gt--, i);
            } else {
                i++;
            }
        }
        QSort(nums, low, lt - 1);
        QSort(nums, gt + 1, high);
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }