Machine Learning - Andrew Ng 随笔

吴恩达这个是真正的完全0基础入门的机器学习课程?。

1 Welcome

Machine Learning定义 ：
A computer program is said to learn from experience E with respect to some task T and some performace measure P, if its performance on T, as measured by P, improves with experience E
举例子：手动标记你的Email为垃圾邮件，系统会学习垃圾如何过滤垃圾邮件。这里的Task就是“分类垃圾邮件”，Experience就是“观察用户如何标记垃圾邮件”，Performance就是“将垃圾邮件分类准确”。
（在RL里面的T、E、P有点像Action，State，Reward，但和其他算法不同的是RL是利用这几个值来对自身进行改进的）

2 Cost Function

他用了线性回归问题举例子，线性回归的目标就是找到对应的θ0、θ1、θ2等的值使cost function最小，前面的1/2m是为了除个样本数再除个2好用于有一个统一的标准，下面这个是简单(一元)线性回归的例子，多元的话就是扩展到多个θx：

（本来没打算看这个但是猛的想起来这个东西和Principle Contents Analysis有点像，只是线性回归是要函数预测值和函数上的差距最小，而PCA降维的方式是各点垂直到函数上的距离最小，而且PCA图上的点就是输出值，他们只是有点像但不一样。）
第一个线性回归，第二个PCA：


使线性回归的cost functions最小可以用梯度下降法，这里的:=是赋值运算符,α在这是learning rate学习率，也是一个hyperparameter超参数（超参数其实可以形象的说是你写函数的时候在参数列表里会有的，而真的参数其实只是超参数之一以矩阵形式传入，就像kNN算法的k值一样），剩下后面的那块东西就是所谓的梯度（在多元里面是多个对θ求偏导数的向量，一般记为▽J）（你只要记得这个值永远与最低的方向相反所以才叫梯度就行了）了:

通过这个GIF可以看看他寻找梯度的过程，虽然只有两个θ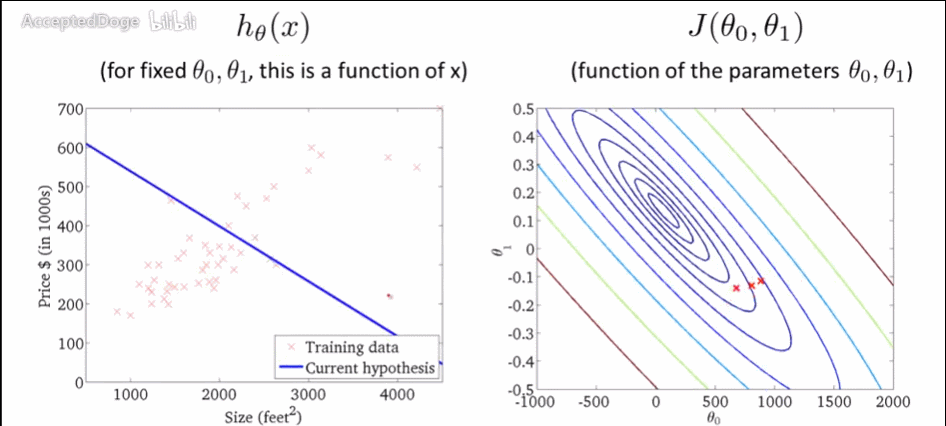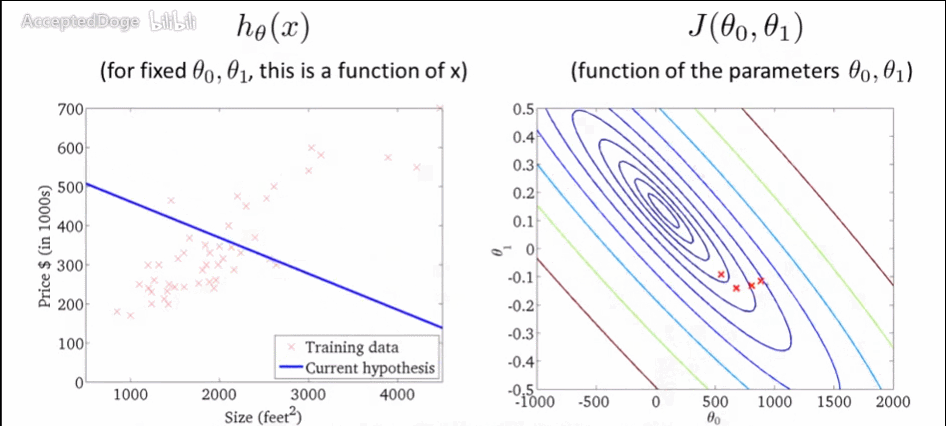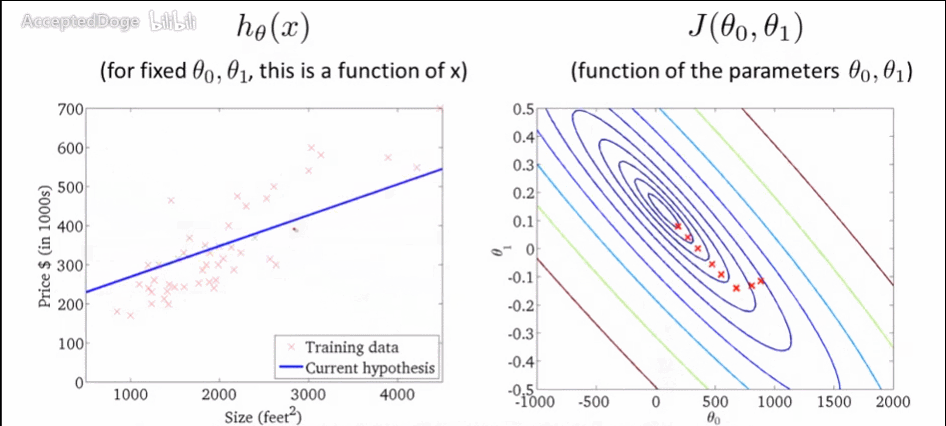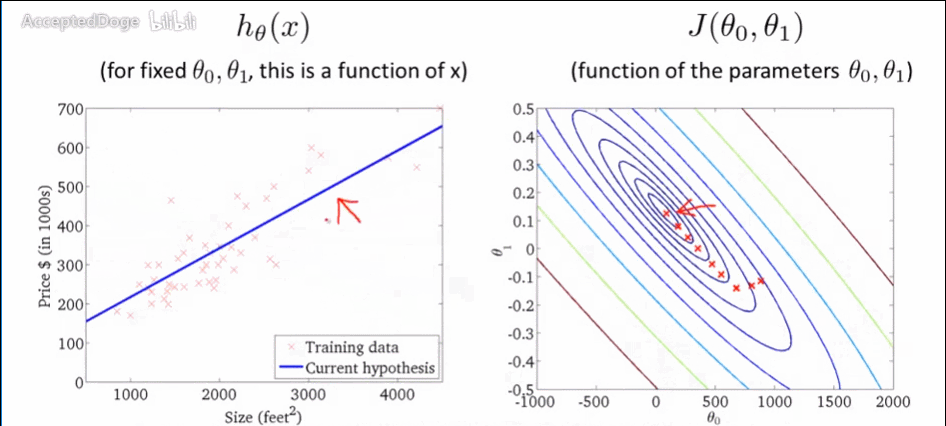
但这种梯度下降（叫Batch Gradient Descent批量梯度下降）行不通，当是标准的凸函数的时候，只有一个全局最小解就有用，但对于有局部最优解的时候就没用了，那么可以用到随机梯度下降法了。

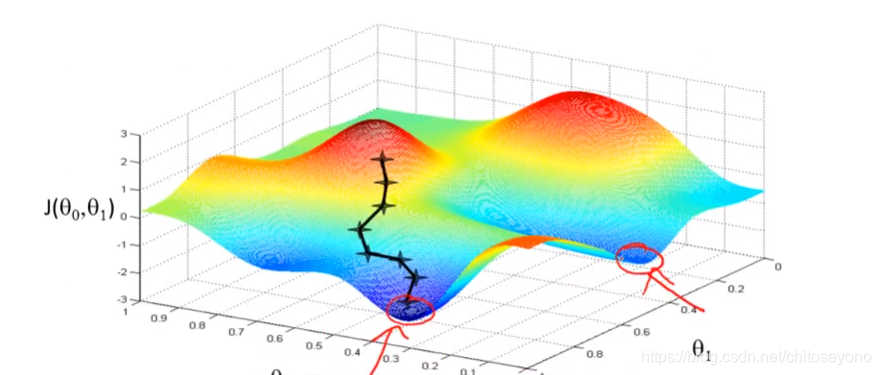
而且虽然现在只有θ0，θ1，但是真正用到的时候会有很多个θ，很多个参数，那么不可能把他们都当做函数的参数，所以就需要将这些θ和x都放进向量，矩阵里面去，不仅方便计算（像能得出Normal Equation正规方程解）也方便看（可以通过巧妙的向量化处理将式子变得简洁且好用）。

3 Review Linear Algebra

第三章好像就是复习一下线代的东西（这也是为什么这节课是0基础就能用的），看一看感觉可以涨术语，像这种：

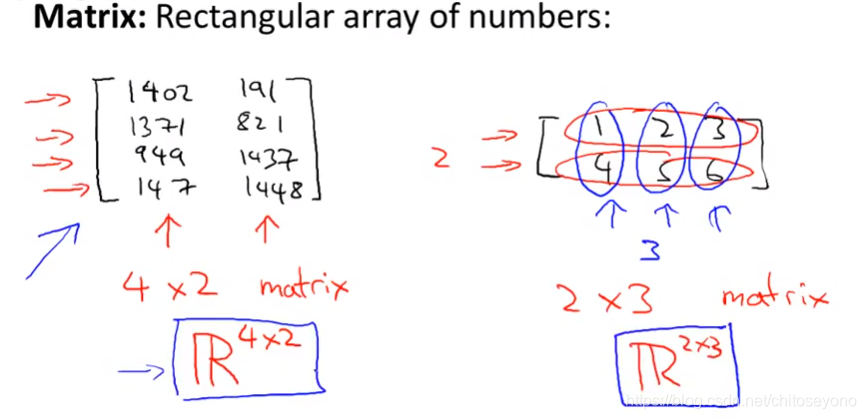
其他都是线代基础了，记一些有用的东西：

1. 只有方阵拥有逆矩阵，方阵A在numpy中用linalg.inv(A)求得A逆
2. 但非方阵有伪逆矩阵，方阵B在numpy中用linalg.pinv(B)求得B逆
3. 转置运算如这张图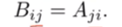，方阵A直接A.T可获得A的转置B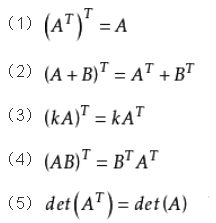
4. 

第四单元讲安装MATLAB和Ocetex，跳了

5 Multivariate Linear Regression

Feature Scaling数值标准化：使每个特征都在一个标准下，使各特征影响力相同，不从数值上使某个特征影响力区别于其他的特征。
Mean Normalization数值归一化：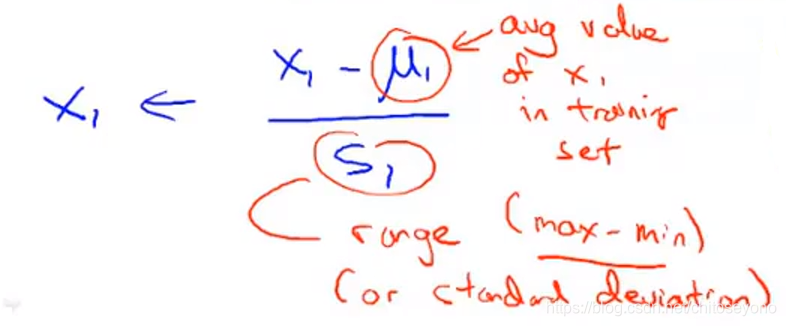
μi为特征Xi的平均数，Si为Xmax-Xmin（最值归一化，更适合于分布有明显边界的情况）或者X的方差（均值方差归一化，适用于有极端值的情况）

▽J should decrease after every iteration多元线性回归中选择α学习率是个学问，大了不收敛，小了收敛太慢。
为了确定▽J是否已经收敛，可以通过选择ε值，小于这个值则认为收敛（所以ε也能当一个超参数）

拟合线性回归Tips：

1. 像长和宽是两个特征，乘在一起变成面积就是一个特征，特征少了更方便
2. 可能不能只是一次方程，或者是二次三次的甚至有根号的特征方程会更加拟合数据，这种时候只需要将特征的定义改一改（如图x2=x²）就能拟合于线性回归中。可能不能只是一次方程，或者是二次三次的甚至有根号的特征方程会更加拟合数据，这种时候只需要将特征的定义改一改（如图x2=x²）就能拟合于线性回归中，这就是多项式回归，实际上就是通过对样本进行升维拉伸使原来线性不可分的变成线性可分
   
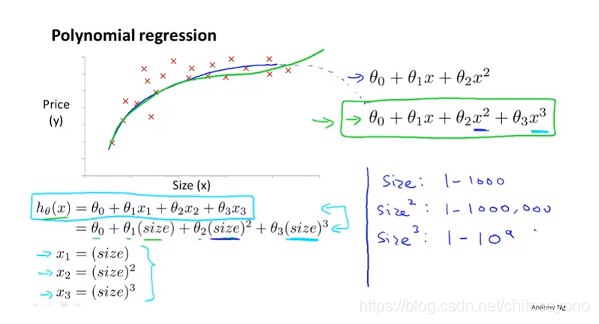
3. 当样本数太少反而特征数过多，应删减一些特征数（降维，正则化）

Normal Function线性回归正规方程解：
通过cost function ▽J将y的值代进去之后实际上可以推导出对θ（指θ0,θ1,θ2…θn的向量）的公式运算法，被称为Normal function，虽然他看起来又短又方便，还是有缺点就是慢O（n^3）

第六单元还是讲MATLAB和Ocetex，跳

7 Logistic Regression

决策边界Decision Boundary
分类问题中的分界线（这根线不取决于数据集，只是取决于那些θ），举两个例子：

1. x1+x2=3
   
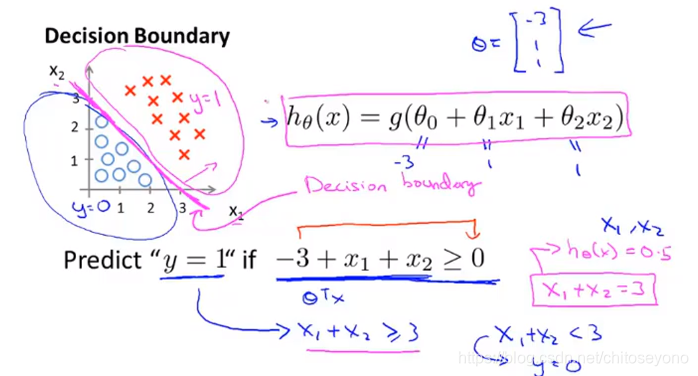
2. x1²+x2²=1
   逻辑回归
   虽说可以用Linear Regression设置阈值的方式来进行二分类问题，但是often isn’t a great idea，不仅因为函数直线容易受极端值影响，而且得到的值是(-∞,+∞)的（我们需要[0,1]的概率），而二分类里label只有0和1两个离散值，所以可以给他包装个g(z)变成Logistic Regression来解决binary classification问题（这个g函数叫sigmoid函数也叫logistic函数）：
   
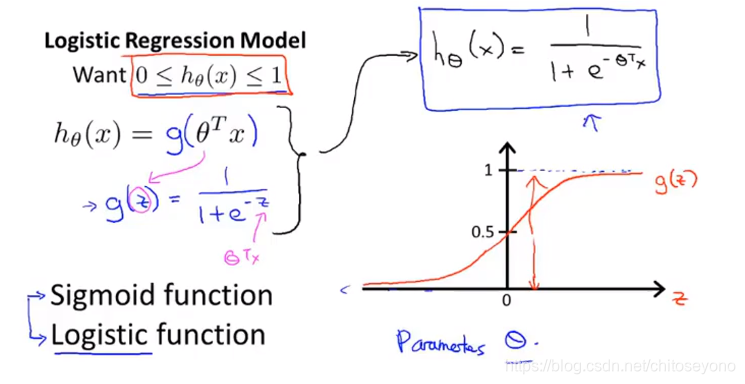
   然后他的损失函数J跟线性回归挺大不同（当y应为1的时候，值越接近0惩罚越大；y应为0的时候，值越接近1惩罚越大）：
   
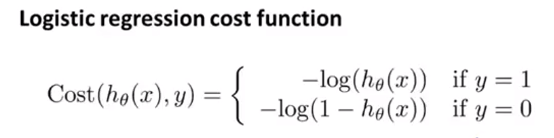
   巧妙地可以简化他变成这样：
   
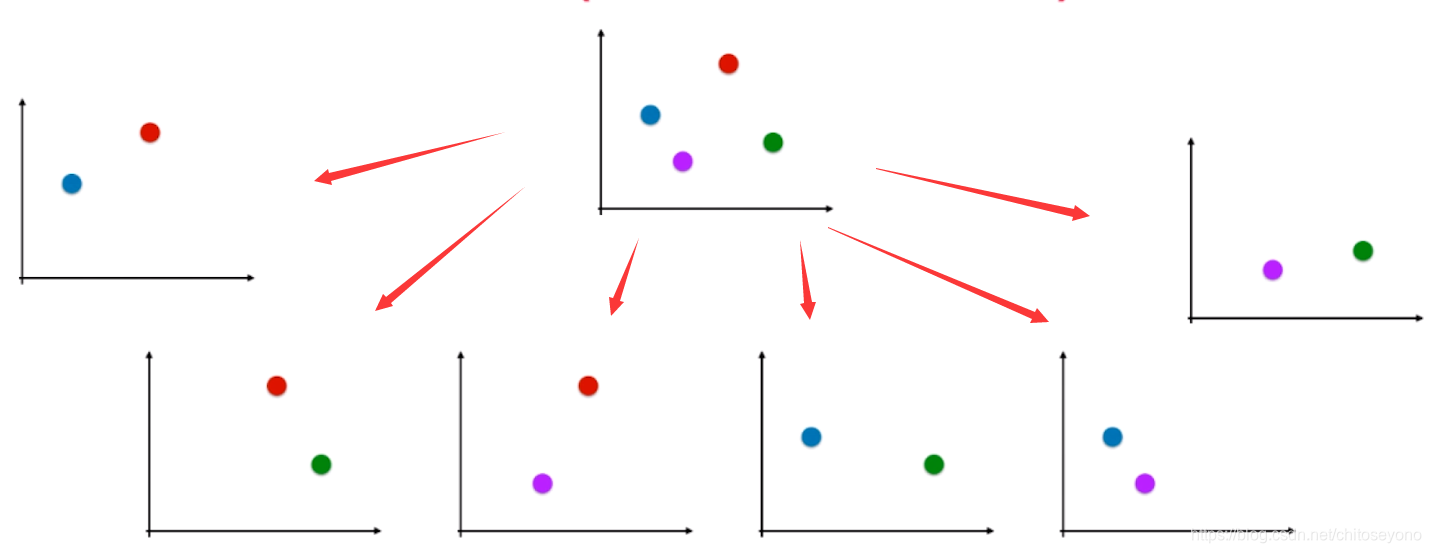
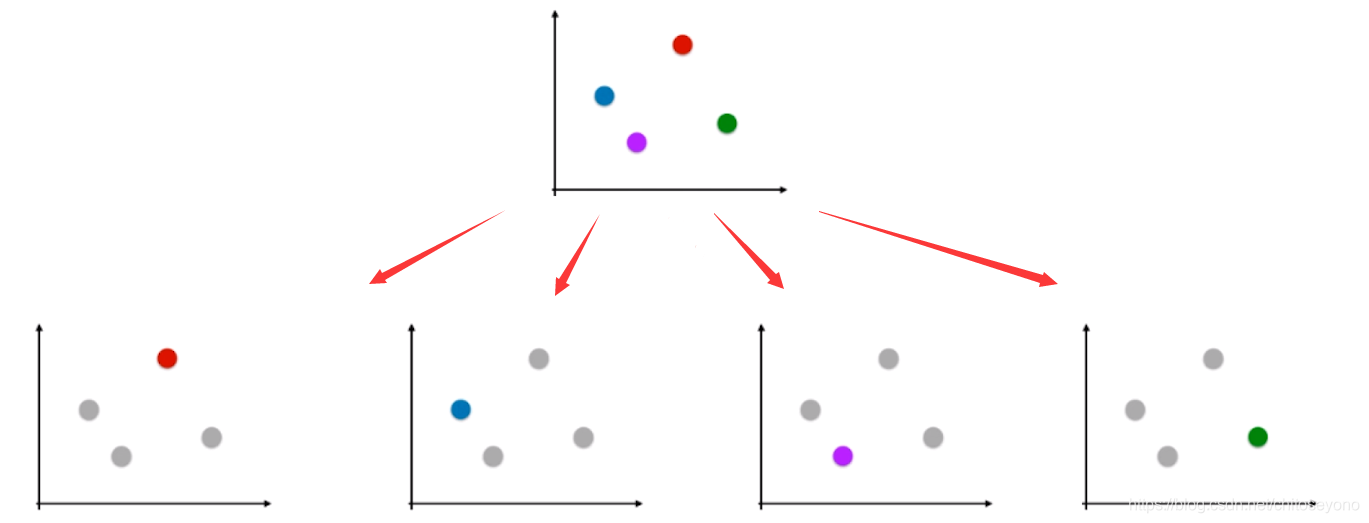
   二分类转多分类问题
   OvO，准确，但时间复杂度大C(n,2)：
   
   OvR：
   

8 Regularzation

High Bias ↔ High Variance => Underfitting ↔ Overfitting（三张图分别是欠拟合，拟合的完美，过拟合）

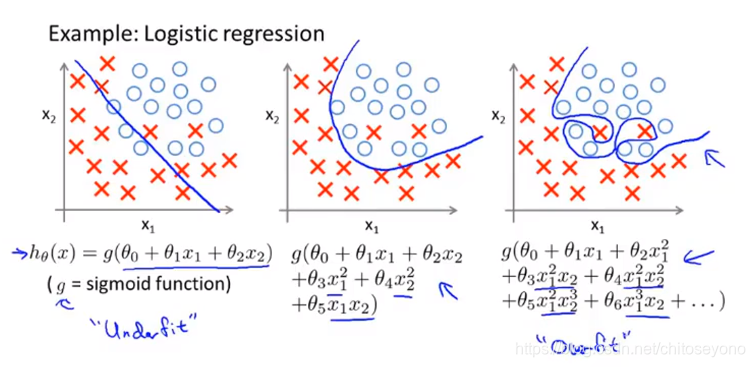
正则化主要是为了解决学习算法的过拟合问题，在多项式回归中过拟合的原因主要是算法太过复杂（就是x的次方太大）以至于几乎整根函数贴在所有训练点上。
正则化有挺多方式的：
Ridge Regression岭回归
岭回归的思路就是让θ变小以至于不让模型疯狂抖动，所以会在线性回归的损失函数▽J上加上这个，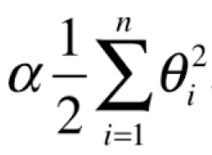
α在这也是一个超参数，正则化参数，α越大，θ就越小，曲线就越平滑，就越不容易过拟合，然后就变成这样：

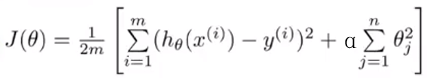
（不过后面加进去的那串里面不包括θ0，他是例外的）
如果是在用Normal Function来解决的话，就变成这样（这里的λ就是前面的α）：

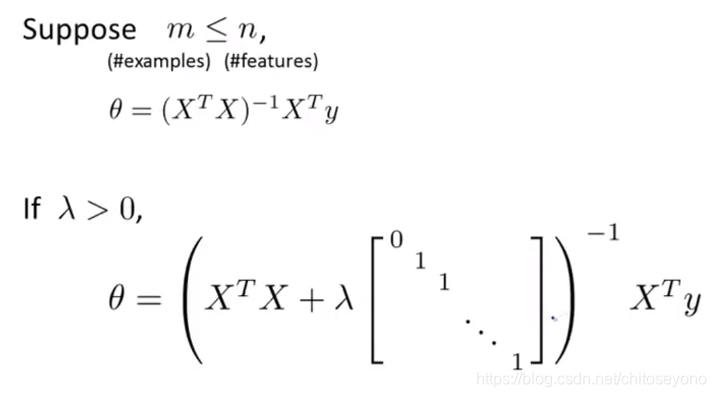
LASSO Regularzation
他的全称好长叫Least Absolute Shrinkage and Selecetion Operator Regression，LASSO其实思路一样，只不过换成了这个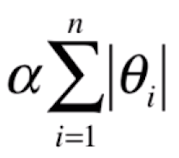
LASSO有点特别，α也是越大的时候曲线越平滑，但他作用更如他的名字一样，他是选择某部分θ值使其变成0，所以他可以作为特征选择用。

在logitstic回归中也可做正则化：

但大部分时候会变成这样子，因为能方便后面的核函数的使用（这里的C就是正则化参数）：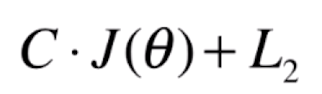

13 Support Vector Machine

看这儿：https://blog.youkuaiyun.com/chitoseyono/article/details/86522249