可持久化线段树(主席树)相关模板题

一、可持久化数组：
题目链接
个人感觉可持久化数据结构的精髓就在于最大限度的使用以前的资源也就是最小的增加新的资源。对于这道题我们可以将原始数组用一个普通线段树来存，当我们需要修改的时候只需要将需要修改的元素在线段树中所在的链修改即可，其他的都可以使用原来的数据。
借用别人的图分析一下：

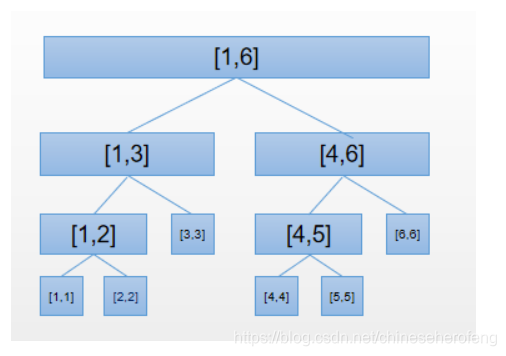
这是原始数据构成的线段树，一共有六个数据。
假如我们需要在此基础上修改第二个元素：

可以看出橙色部分即为我们需要修改的部分

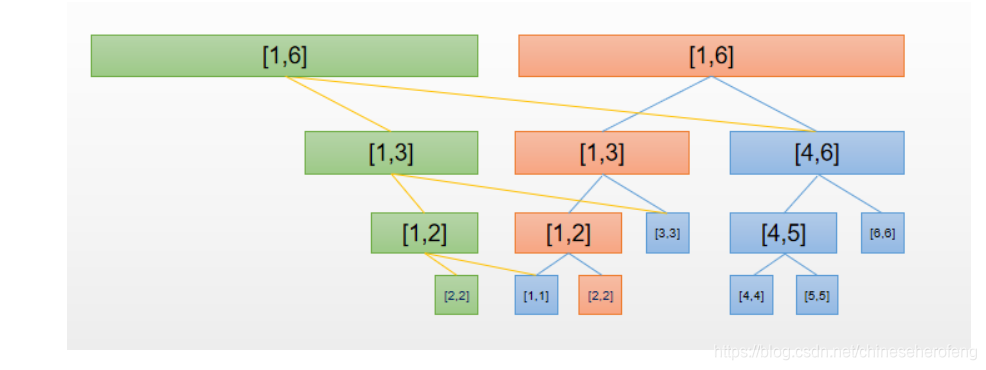
这就是修改了第二个元素以后的可持久化数组的样子，绿色为修改第二个节点后的线段树版本，在修改的同时，也继承了与上一个版本线段树相同的地方，使得新增的节点能够最少。
相关代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>

using namespace std;
const int N = 1e6 + 5;
struct node {
    int l, r, val;
};
node tr[N * 20];
int cnt[N];
int n, m, idx;
int root[N];
int build(int l, int r) {// 建立原始数组线段树
    int pos = ++idx;
    if (l == r) {
        tr[pos] = { l,r,cnt[l] };
        return pos;
    }
    else {
        int mid = l + r >> 1;
        tr[pos].l = build(l, mid);
        tr[pos].r = build(mid + 1, r);
        return pos;
    }
}
int update(int pre, int l, int r, int pos, int val) {// 每进行一次修改操作更新一次
    int poss = ++idx;
    tr[poss].l = tr[pre].l, tr[poss].r = tr[pre].r, tr[poss].val = tr[pre].val;// 继承之前版本线段树
    if (tr[pre].l == tr[pre].r) {// 找到需要修改的元素进行修改，并返回该节点下标
        tr[poss] = { poss,poss,val };
        return poss;
    }
    int mid = l + r >> 1;
    // 动态开点，对线段树进行修改
    if (pos <= mid) tr[poss].l = update(tr[pre].l, l, mid, pos, val);
    else tr[poss].r = update(tr[pre].r, mid + 1, r, pos, val);
    return poss;
}
int query(int now, int l, int r, int pos) {
    if (l == r) return tr[now].val;
    int mid = l + r >> 1;
    if (pos <= mid) return query(tr[now].l, l, mid, pos);
    else return query(tr[now].r, mid + 1, r, pos);
}
int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &cnt[i]);
    root[0] = build(1, n);
    for (int i = 1; i <= m; i++) {
        int a, b; scanf("%d %d", &a, &b);
        if (b == 1) {
            int pos, val; scanf("%d %d", &pos, &val);
            root[i] = update(root[a], 1, n, pos, val);
        }
        else {
            int pos; scanf("%d", &pos);
            int ans = query(root[a], 1, n, pos);
            root[i] = root[a];
            printf("%d\n", ans);
        }
    }
    return 0;
}

二、权值线段树上进行可持久化
题目链接
前言：
权值线段树：与不同线段树不同，权值线段树的节点存的是一段值域区间，而不是下标区间，权值线段树的节点一般可维护数组中值在一段值域区间的元素个数等。
因为不同数的值差别可能很大，可能会导致权值线段树维护的值域也相应增大，所以在建立权值线段树之前可以考虑先将数据离散化，便于权值线段树维护值域。

对于本题叫我们求出区间第K的数，我们就可以考虑使用权值线段树维护值域区间元素个数，那怎么找第K个呢，我们很容易想到权值线段树的值域是单调递增的，于是理所当然的可以使用二分查找。假设当前值域为(l,r),枚举值域中点mid，如果在值域(l,mid)的元素个数小于等于K的话说明第K大数在(l,mid)，反之第K大数在(mid+1,r)，直到找到为止。
相关代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
const int N = 1e5+5;
struct node{
    int l,r,num;
};
node tr[N*20];
int n,m,idx;
int root[N];
vector<int> res;
int cnt[N];
int build(int l,int r) {
    int pos=++idx;
    if(l==r) {
        tr[pos]={pos,pos,0};
        return pos;
    }
    else {
        int mid=l+r>>1;
        tr[pos].l=build(l,mid);
        tr[pos].r=build(mid+1,r);
        tr[pos].num=0;
        return pos;
    }
}
int update(int pre,int l,int r,int val) {
    int pos=++idx;
    tr[pos].l=tr[pre].l,tr[pos].r=tr[pre].r,tr[pos].num=tr[pre].num+1;//  继承之前版本权值线段树的信息
    if(l<r) {
        int mid=l+r>>1;
        //  动态开点， 将与之前权值线段树版本不同的信息，另开一条链
        if(val<=mid) tr[pos].l=update(tr[pre].l,l,mid,val);
        else tr[pos].r=update(tr[pre].r,mid+1,r,val);
    }
    return pos;
}
int query(int pre,int now,int l,int r,int pri) {
    if(l==r) return l;
    int mid=l+r>>1;
    int sum=tr[tr[now].l].num-tr[tr[pre].l].num;//  对应段值相减，类似处理前缀(先判断左区间)
    if(pri<=sum) return query(tr[pre].l,tr[now].l,l,mid,pri);
    else return query(tr[pre].r,tr[now].r,mid+1,r,pri-sum);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) {
        int a; cin>>a;
        cnt[i]=a;
        res.push_back(a);
    }
    sort(res.begin(),res.end());
    res.erase(unique(res.begin(),res.end()),res.end());
    for(int i=1;i<=n;i++) {
        int pos=lower_bound(res.begin(),res.end(),cnt[i])-res.begin();
        cnt[i]=pos+1;
    }
    int len=res.size();
    root[0]=build(1,len);
    for(int i=1;i<=n;i++) 
        root[i]=update(root[i-1],1,len,cnt[i]);
    while(m--) {
        int l,r,k; cin>>l>>r>>k;
        int ans=query(root[l-1],root[r],1,len,k);
        cout<<res[ans-1]<<endl;
    }
    return 0;
}