kmp算法

核心思想

要获得前缀 和 后缀的最长共有元素的长度。
所以要开一个next[]数组记录字符串str在i位置的后缀和前缀字符串相同长度,即ne[i]中存的是str中最长前缀的最后一个字符的下标.
比如 字符串str为:abaab

	a	b	a	a	b
i(下标)	1	2	3	4	5
ne[i]	0	0	1	1	2

i=1时 无前缀存所以ne[1]=0.

i=2 时 其前缀为a和后缀b不相等 所以ne[2]=0
i=3时 发现他的一个后缀a和str 的一个前缀a相同 而前缀a最后一个字符的下标为1 所以ne[3]=1;
i=4时 同i=3时 ne[4]=1;
i=5时 后缀ab和前缀ab相同 b下标为2所以ne[5]=2;
备注:个人习惯存储字符串从下表1开始存储.

为什么要对模板串进行预处理呢

如图,当模式串s和模板穿b进行匹配的时候,匹配到a时之前都相同,但s的下一个是’c’,b的下一个是’d’.这将导致匹配失败.但已经匹配的部分放弃的话将导致性能浪费,那该怎么进行优化呢.
如果此时我们能获得他的后缀(从匹配时的不相同位置之前的位置开始的后缀)和他的前缀(指从i=1时开始的前缀)相等的长度,然后把前缀移到后缀这个位置,不就不用重新开始匹配了吗(指bf算法的思想).
比如说

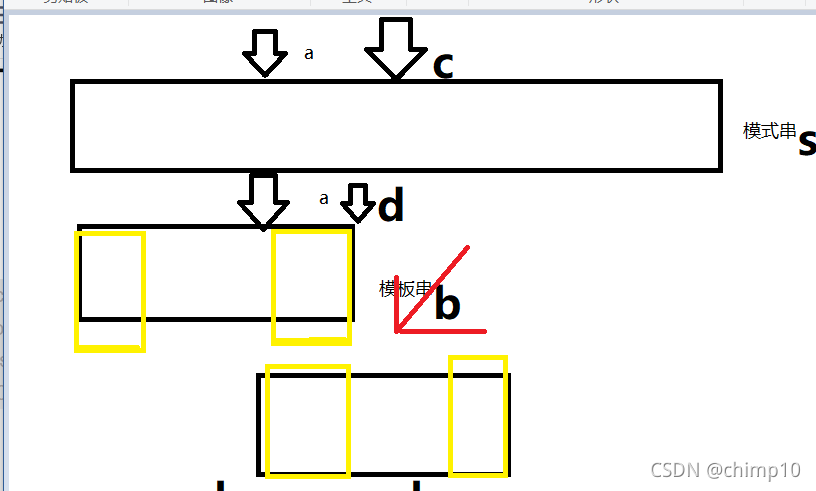
黄色部分指相同的前缀和后缀 ,将模板串右滑到如图所示的位置(前缀右滑到和后缀相同的位置)然后在从红箭头所指的位置继续开始匹配
然后就有了kmp算法和ne[i]数组

练手的题目

acwing 831.kmp 纯裸题
题目链接
附上ac的代码
不要直接抄代码哦

#include<stdio.h>
#include<iostream>
#include<string>

using namespace std;


int main()
{
    
    int n,m;
    char s[1001000],p[100100];
    int ne[(int) 1e5+10];
    cin>>n>>p+1>>m>>s+1;
    int i,j=0;
    for(i=2;i<=n;++i)
    {
        while(j&&p[i]!=p[j+1]) j=ne[j];
        if(p[i]==p[j+1]) ++j;
        ne[i]=j;

    }
   
    for(i=1,j=0;i<=m;++i)
    {
       while(j&&s[i]!=p[j+1]) j=ne[j];
        if(s[i]==p[j+1]) ++j;
        if(j==n)
        {
            cout<<i-n<<" ";
            j=ne[j];
        }

    }
    //system("pause");
    return 0;
    

    
}