算法面试必刷：双指针8道高频例题全解析（附最优代码）

原创已于 2025-11-15 18:42:21 修改 · 848 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #面试 #数据结构 #c++ #后端 #开发语言

于 2025-11-15 18:18:48 首次发布

算法专题专栏收录该内容

1 篇文章

订阅专栏

LCR179.查找总价格为目标值的两个商品

15. 三数之和

18.四数之和

一、算法简介

常见的双指针有两种形式，⼀种是对撞指针，⼀种是左右指针。

对撞指针：一般用于顺序结构中，也称左右指针。

对撞指针从两端向中间移动。⼀个指针从最左端开始，另⼀个从最右端开始，然后逐渐往中间逼近。
对撞指针的终⽌条件⼀般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循环），也就是：

left == right （两个指针指向同⼀个位置）
left > right （两个指针错开）

快慢指针：又称为龟兔赛跑算法，其基本思想就是使用两个移动速度不同的指针在数组或链表等序列结构上移动。

这种⽅法对于处理环形链表或数组非常有用。其实不单单是环形链表或者是数组，如果我们要研究的问题出现循环往复的情况时，均可考虑使用快慢指针的思想。

快慢指针的实现⽅式有很多种，最常⽤的⼀种就是：

在⼀次循环中，每次让慢的指针向后移动⼀位，⽽快的指针往后移动两位，实现⼀快⼀慢。

算法题

283.移动零

https://leetcode.cn/problems/move-zeroes/

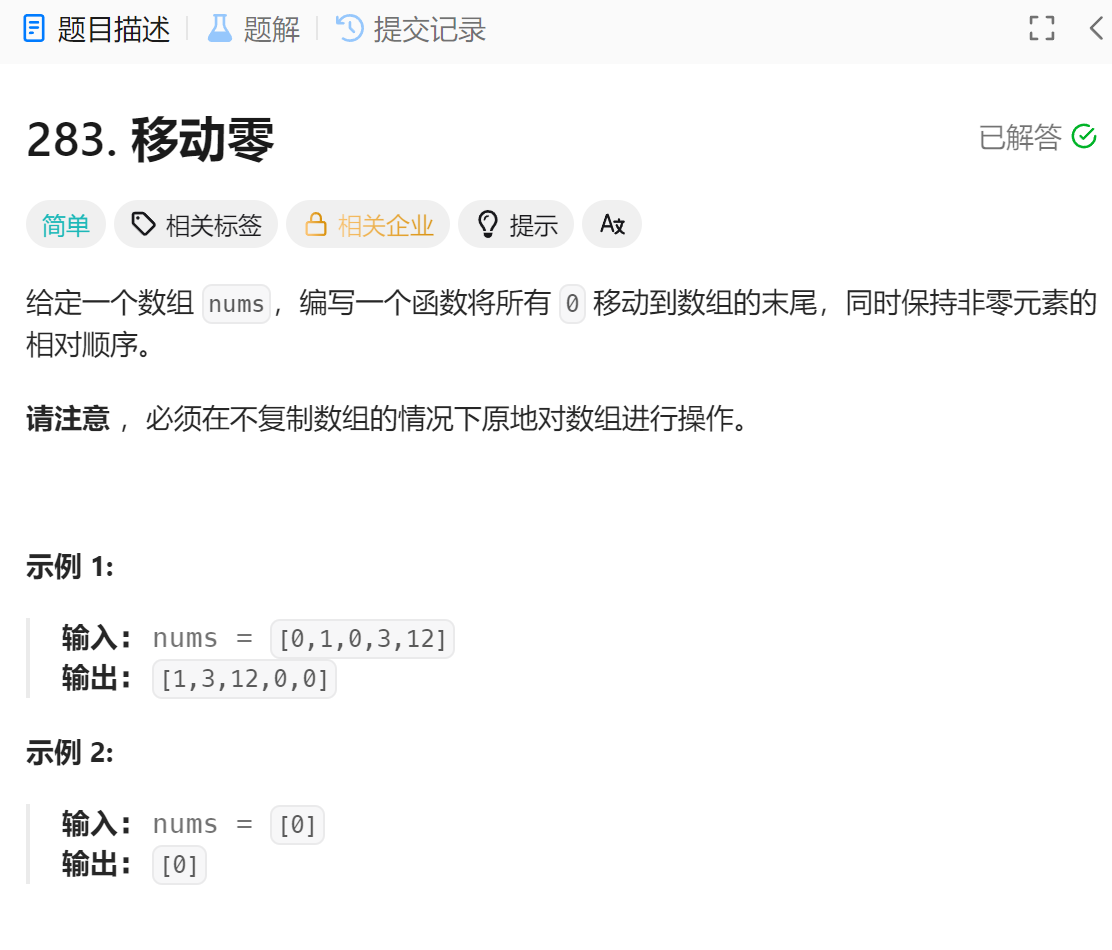
数组分两块是非常常见的⼀种题型，主要就是根据⼀种划分⽅式，将数组的内容分成左右两部
分。这种类型的题，⼀般就是使⽤「双指针」来解决。

这道题我们就是通过指针将数组分为了两类，一类是0，一类是其他。

算法思路：在本题中，我们可以⽤⼀个cur 指针来扫描整个数组，另⼀个dest 指针⽤来记录⾮零数序列的最后⼀个位置。根据cur 在扫描的过程中，遇到的不同情况，分类处理，实现数组的划分。

在cur 遍历期间，使[0, dest] 的元素全部都是⾮零元素， [dest + 1, cur - 1] 的元素全是零。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
    for(int cur=0,dest=-1;cur<nums.size();cur++)
        if(nums[cur]!=0)
            swap(nums[++dest],nums[cur]);
           
        
    }
};

1089.复写零

https://leetcode.cn/problems/duplicate-zeros/description/

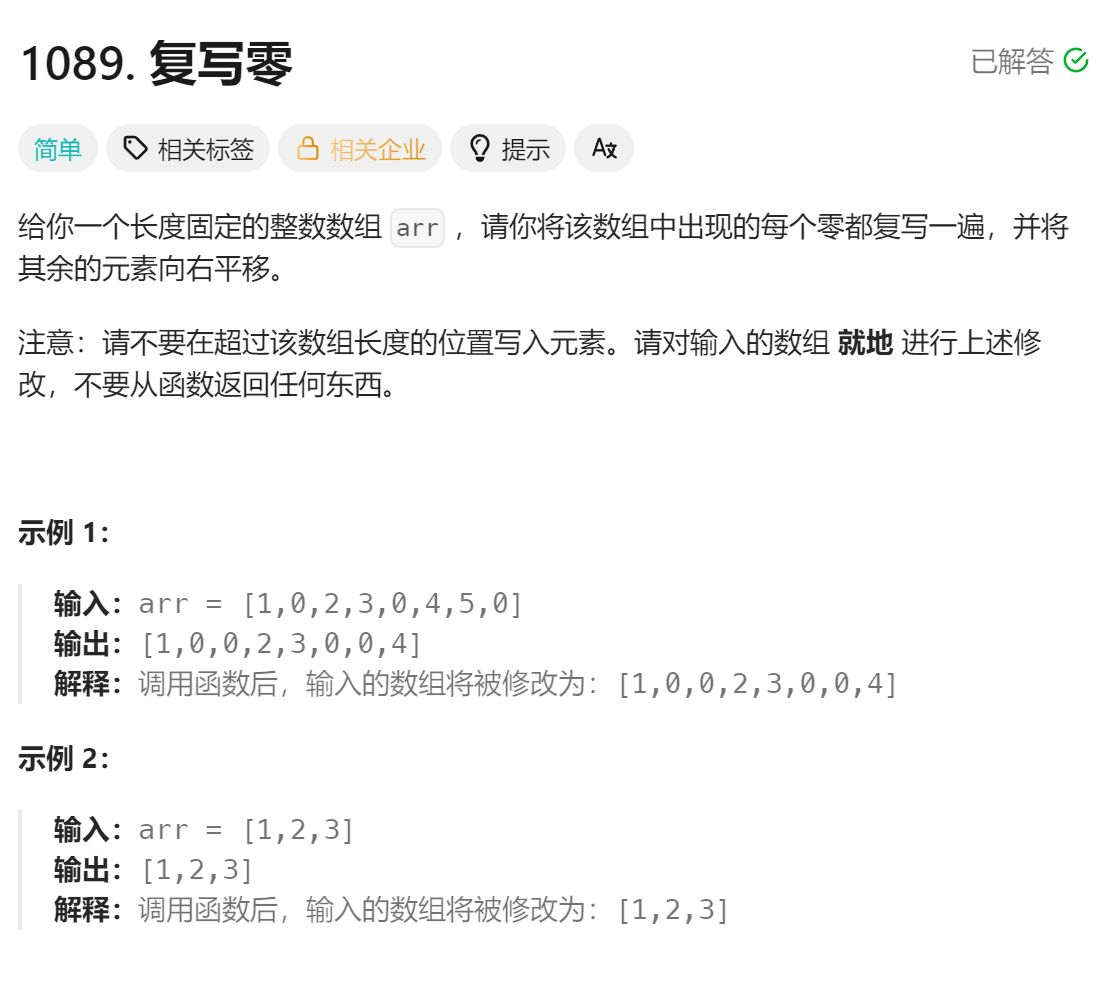
算法思路：
如果「从前向后」进⾏原地复写操作的话，由于0的出现会复写两次，导致没有复写的数「被覆盖掉」。因此我们选择「从后往前」的复写策略。
但是「从后向前」复写的时候，我们需要找到「最后⼀个复写的数」，因此我们的⼤体流程分两步：
i. 先找到最后⼀个复写的数；
ii. 然后从后向前进行复写操作。

class Solution 
{
public:
 void duplicateZeros(vector<int>& arr) 
 {
 // 1. 先找到最后⼀个数 
 int cur = 0, dest = -1, n = arr.size();
 while(cur < n)
 {
 if(arr[cur]) dest++;
 else dest += 2;
 if(dest >= n - 1) break;
 cur++;
 }
 // 2. 处理⼀下边界情况 
 if(dest == n)
 {
 arr[n - 1] = 0;
 cur--; dest -=2;
 }
 // 3. 从后向前完成复写操作 
 while(cur >= 0)
 {
 if(arr[cur]) arr[dest--] = arr[cur--];
 else
 {
 arr[dest--] = 0;
 arr[dest--] = 0;
 cur--;
 }
 }
 }
};

202. 快乐数

https://leetcode.cn/problems/happy-number/description/

根据上述的题⽬分析，我们可以知道，当重复执⾏x 的时候，数据会陷⼊到⼀个「循环」之中。⽽「快慢指针」有⼀个特性，就是在⼀个圆圈中，快指针总是会追上慢指针的，也就是说他们总会相遇在⼀个位置上。如果相遇位置的值是1 ，那么这个数⼀定是快乐数；如果相遇位置不是1 的话，那么就不是快乐数。

class Solution 
{
public:
 int bitSum(int n) // 返回 n 这个数每⼀位上的平⽅和{ 
 int sum = 0;
 while(n)
 {
 int t = n % 10;
 sum += t * t;
 n /= 10;
 }
 return sum;
 }
 bool isHappy(int n) 
 {
 int slow = n, fast = bitSum(n);
 while(slow != fast)
 {
 slow = bitSum(slow);
 fast = bitSum(bitSum(fast));
 }
 return slow == 1;
 }
};

11.盛最多水的容器

https://leetcode.cn/problems/container-with-most-water/description/

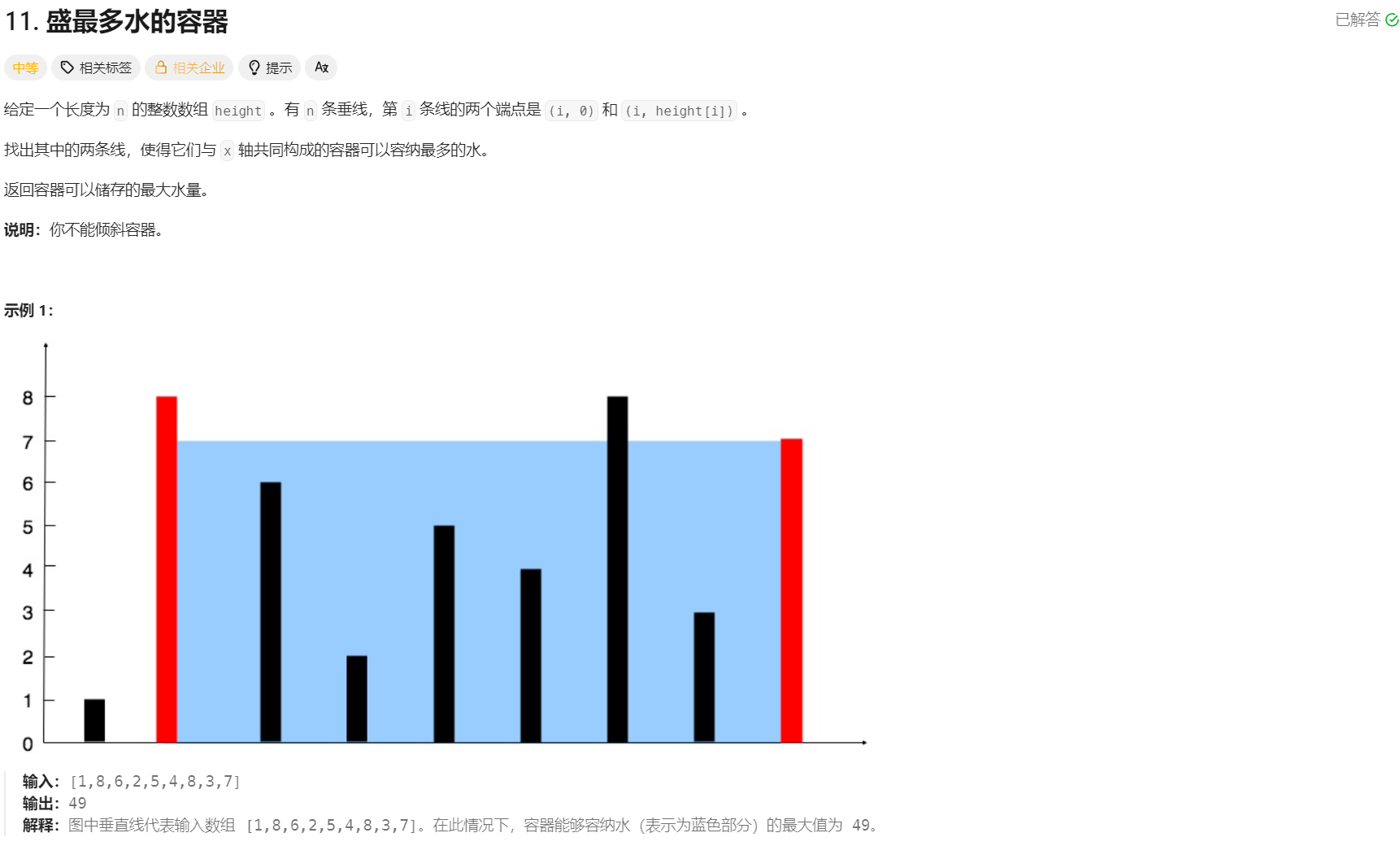
算法思路：

第一种，穷举所有的结果，但是这测试了会超时。

第二种，对撞指针

设两个指针left ，right 分别指向容器的左右两个端点，此时容器的容积:
v = (right - left) * min( height[right], height[left])
容器的左边界为height[left] ，右边界为height[right] 。
为了⽅便叙述，我们假设「左边边界」⼩于「右边边界」。
如果此时我们固定⼀个边界，改变另⼀个边界，⽔的容积会有如下变化形式：
容器的宽度⼀定会随着变⼩。
由于左边界较⼩，决定了水的⾼度。如果改变左边界，新的⽔⾯⾼度不确定，但是⼀定不会超过右边的柱⼦⾼度，因此容器的容积可能会增⼤。
如果改变右边界，⽆论右边界移动到哪⾥，新的⽔⾯的⾼度⼀定不会超过左边界，也就是不会超过现在的⽔⾯⾼度，但是由于容器的宽度减⼩，因此容器的容积⼀定会变⼩的。
由此可⻅，左边界和其余边界的组合情况都可以舍去。所以我们可以left++ 跳过这个边界，继续去判断下⼀个左右边界。

总的来说，我们把两者中的长的固定了，短的就不用去判断了
当我们不断重复上述过程，每次都可以舍去⼤量不必要的枚举过程，直到left 与right 相
遇。期间产⽣的所有的容积里面的最⼤值，就是最终答案。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left=0,right=height.size()-1,ret=0;
        while(left<right){
            int v=min(height[left],height[right])*(right-left);
           ret=max(ret,v);
           if(height[left]<height[right]) left++;
           else right--;
        }
        return ret;
    }
};

611. 有效三⻆形的个数

https://leetcode.cn/problems/valid-triangle-number/

先将数组排序。根据上题最多水的容器中的优化思想，我们可以固定⼀个「最⻓边」，然后在⽐这条边⼩的有序数组中找出⼀个⼆元组，使这个⼆元组之和⼤于这个最⻓边。由于数组是有序的，我们可以利⽤「对撞指针」来优化。设最⻓边枚举到i 位置，区间[left, right] 是i 位置左边的区间（也就是⽐它⼩的区间）：

◦ 如果nums[left] + nums[right] > nums[i] ：

▪ 说明[left, right - 1] 区间上的所有元素均可以与nums[right] 构成⽐ nums[i] ⼤的⼆元组

▪ 满⾜条件的有right - left 种 ▪此时right 位置的元素的所有情况相当于全部考虑完毕，

right-- ，进⼊下⼀轮判断

◦ 如果nums[left] + nums[right] ：

▪ 说明left 位置的元素是不可能与[left + 1, right] 位置上的元素构成满⾜条件的⼆元组

▪ left 位置的元素可以舍去， left++ 进⼊下轮循环

class Solution 
{
public:
 int triangleNumber(vector<int>& nums) 
 {
 // 1. 优化 
 sort(nums.begin(), nums.end());
 // 2. 利⽤双指针解决问题 
 int ret = 0, n = nums.size();
 for(int i = n - 1; i >= 2; i--) // 先固定最⼤的数 
 {
 // 利⽤双指针快速统计符合要求的三元组的个数 
 int left = 0, right = i - 1;
 while(left < right)
 {
 if(nums[left] + nums[right] > nums[i])
 {
 ret += right - left;
 right--;
 }
 else
 {
 left++;
 }
 }
 }
 return ret;
 }
};

LCR179.查找总价格为目标值的两个商品

https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/

注意到本题是升序的数组，因此可以⽤「对撞指针」优化时间复杂度。

这里和上题所用思路一样，也是取长，不判断短的，减少轮询来减少时间复杂度。

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left=0, right=price.size()-1;
        while(left<right){
            int sum=price[left]+price[right];
            if(sum>target) right--;
            else if(sum<target) left++;
            else return {price[left],price[right]};
        }
        return {-4941, -1};
    }


};

为了照顾编译器，我们还需要写这句： return {-4941, -1};

15. 三数之和

https://leetcode.cn/problems/3sum/description/

思路：

i.先排序；

ii. 然后固定⼀个数a ：

iii. 在这个数后⾯的区间内，使⽤「双指针算法」快速找到两个数之和等于-a 即可。

但是要注意的是，这道题⾥⾯需要有「去重」操作 i. 找到⼀个结果之后， left 和right 指针要「跳过重复」的元素； ii. 当使⽤完⼀次双指针算法之后，固定的a 也要「跳过重复」的元素。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ret;  // 存储最终结果：所有和为0的不重复三元组
        sort(nums.begin(), nums.end());  // 排序预处理：1.便于去重 2.为双指针移动提供条件
        
        int n = nums.size();
        // 外层循环：固定三元组中的第一个元素 nums[i]
        for (int i = 0; i < n; ) {
            // 优化：若第一个元素已大于0，由于数组递增，后续三数之和必大于0，直接退出
            if (nums[i] > 0) break;
            
            // 双指针初始化：left指向i的下一个元素，right指向数组末尾
            int left = i + 1, right = n - 1;
            // 目标值：另外两个元素的和需等于 -nums[i]（才能满足三数之和为0）
            int target = -nums[i];
            
            // 双指针寻找满足条件的另外两个元素
            while (left < right) {
                int sum = nums[left] + nums[right];  // 计算当前双指针元素的和
                
                if (sum < target) {
                    // 和小于目标值，需增大总和，左指针右移（数组递增，右移后值更大）
                    left++;
                } else if (sum > target) {
                    // 和大于目标值，需减小总和，右指针左移（左移后值更小）
                    right--;
                } else {
                    // 找到一组满足条件的三元组，加入结果集
                    ret.push_back({nums[i], nums[left], nums[right]});
                    
                    // 移动双指针，继续寻找其他可能的组合
                    left++;
                    right--;
                    
                    // 去重：跳过左指针相同的元素（避免重复三元组）
                    while (left < right && nums[left] == nums[left - 1]) {
                        left++;
                    }
                    // 去重：跳过右指针相同的元素（避免重复三元组）
                    while (left < right && nums[right] == nums[right + 1]) {
                        right--;
                    }
                }
            }
            
            // 移动外层循环指针，处理下一个可能的第一个元素
            i++;
            // 去重：跳过与当前nums[i]相同的元素（避免重复三元组）
            while (i < n && nums[i] == nums[i - 1]) {
                i++;
            }
        }
        
        return ret;  // 返回所有符合条件的三元组
    }
};

18.四数之和

参考三数之和

class Solution 
{
public:
 vector<vector<int>> fourSum(vector<int>& nums, int target) 
 {
 vector<vector<int>> ret;
 // 1. 排序 
 sort(nums.begin(), nums.end());
 // 2. 利⽤双指针解决问题 
 int n = nums.size();
 for(int i = 0; i < n; ) // 固定数 a 
 {
 // 利⽤ 三数之和 
 for(int j = i + 1; j < n; ) // 固定数 b 
 {
 // 双指针 
 int left = j + 1, right = n - 1;
 long long aim = (long long)target - nums[i] - nums[j];
 while(left < right)
 {
 int sum = nums[left] + nums[right];
if(sum < aim) left++;
 else if(sum > aim) right--;
 else
 {
 ret.push_back({nums[i], nums[j], nums[left++], 
nums[right--]});
 // 去重⼀ 
 while(left < right && nums[left] == nums[left - 1]) 
left++;
 while(left < right && nums[right] == nums[right + 1]) 
right--;
 }
 }
 // 去重⼆ 
 j++;
 while(j < n && nums[j] == nums[j - 1]) j++;
 }
 // 去重三 
 i++;
 while(i < n && nums[i] == nums[i - 1]) i++;
 }
 return ret;
 }
};