哈夫曼树和哈弗曼编码

 这里第一步，取出最小权值的c跟d 组成新树，6（这里6是权值，由组成的结点权值相加） 2 4 ，然后再重复造新树 把b拉进来 组成 11 5 6 2 4，一直到权值最高的结点也被拉进来组成新树，最后出来的就是哈夫曼树。

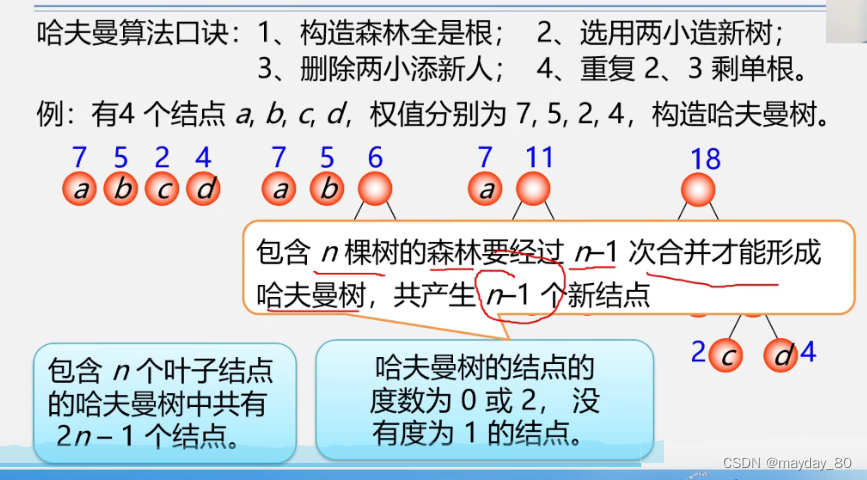
 结点两两相造成新树，n个叶子结点，会结合n-1次，也就生成n-1个节点，再加上本身n个节点。那对应的哈夫曼树就有2n-1个节点 。其中，n-1个结点度为2，n个结点度为0.

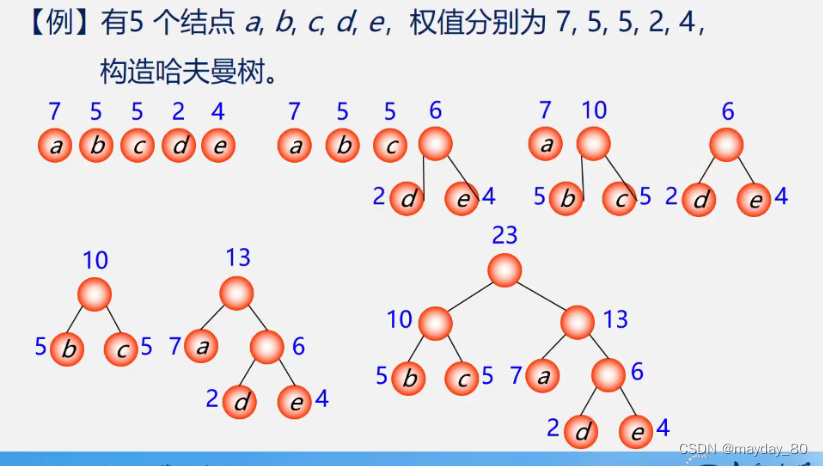
 构造新树是比较当前森林里面最小的权值，拎出来两个，造新树。而不是按顺序就近造。切记切记。

 

 

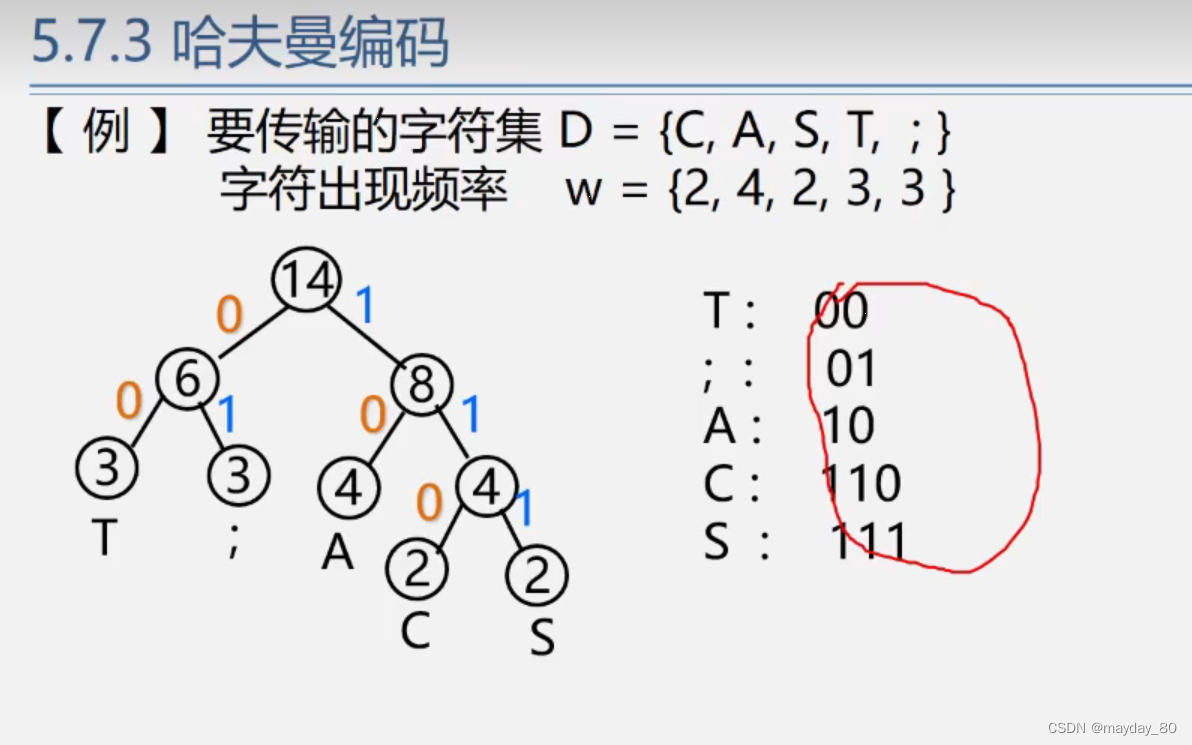
 哈夫曼编码，这个题目中把出现频率看成是权值，通过构建哈夫曼树来确定每个独立结点各自的编码。因为要求是出现频率越大，编码越短，这就符合哈夫曼树的性质。左子树取0，右子树取1。从根节点出发，路径上的结点数字叠加。

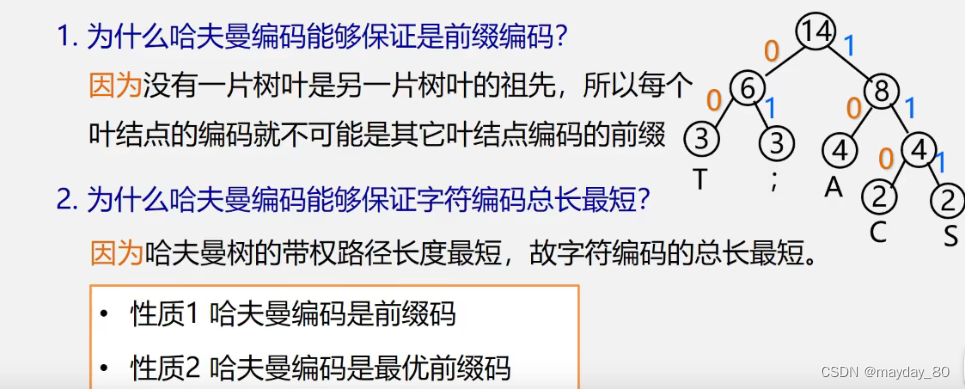
 OKAY。第一个问题解释，因为我们要进行编码的数据，本身就看成是独立的结点，森林中独立的树，各自之间没有联系，所以各自的编码不会是其他结点的前缀。第二个问题解释，这个很好理解了，权值越大的越靠近根节点，路径也就最短。