DeepSeek问答，六千字，浅谈数据库索引技术！_deepseek提问中的有哪些通配符-优快云博客

在这里插入图片描述

浅谈数据库B+ tree索引

一:为什么需要索引?
二:索引为什么选择B+ Trees结构？
三:详细介绍B+ Trees索引?
四:为什么有人说单表超过2000万，数据查询性能会下降？
五:B+ Trees索引为什么对'%xxx%'类型模糊查询不起作用?
六:MySQL和Oracle的B+ tree索引有什么不同？
七:MySQL和达梦数据库索引组织表的区别?

一:为什么需要索引?

在这里插入图片描述

假设电话本里记录了2000000条电话记录，而且是无序的，你要在电话本里找到所有姓名是“张三”的电话号，就算你比较幸运，在第二页就找到了“张三”，但是由于可能会有重名，你需要从第一页翻到最后一页，才能确保找到了所有“张三”的电话号，如何提高查询性能？

在这里插入图片描述

可以想到，对电话本做一个目录，通过目录快速定位到具体人员的电话信息。

而数据库索引就像这个电话本的目录。当你查找某个内容时，目录能帮你快速找到对应的页码，而不需要一页一页翻。同样，数据库索引帮助数据库快速定位数据，避免逐行扫描，从而加快查询速度。

二:索引为什么选择B+ Trees结构？

https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

在这里插入图片描述

B+ Trees 是数据库索引的主流选择，因为它平衡了查询、插入、删除和范围查询的性能，特别适合磁盘存储和大规模数据。

其他数据结构索引在特定场景下可能表现更好，但在通用数据库场景中，B+ Trees的综合性能最优。

以下是 B+树 与 AVL树、二叉树（BST）、红黑树 的对比表格，从多个维度分析它们的优缺点：

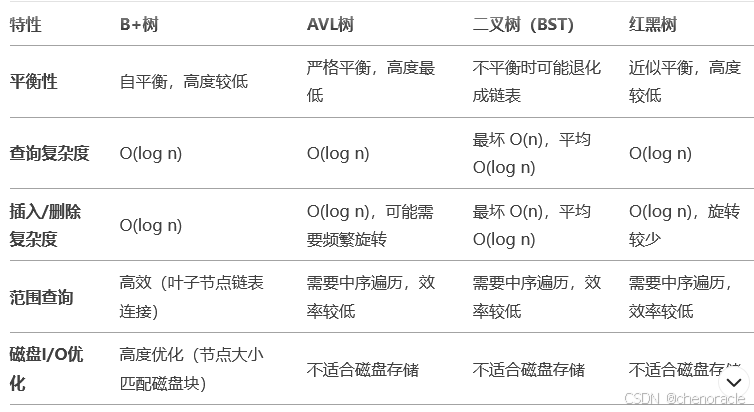
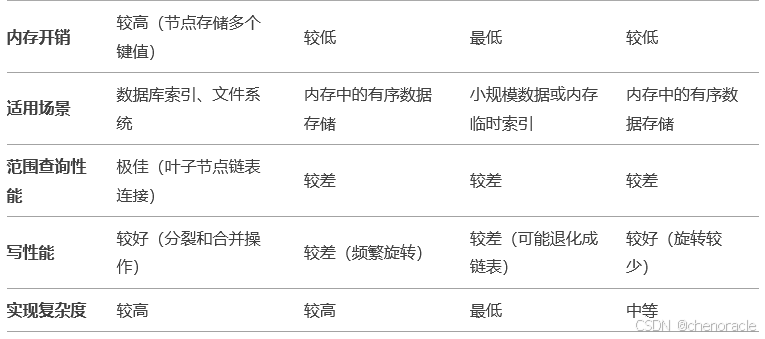
在这里插入图片描述

参考:https://zhuanlan.zhihu.com/p/562512587

二叉树:

二叉树的特点：

1、每个节点最多有两个子树，所以二叉树不存在度大于2的节点（结点的度：结点拥有的子树的数目。），可以没有子树或者一个子树。

2.左子树和右子树有顺序，次序不能任意颠倒。

3、二叉树支持动态的插⼊和查找，保证操作在O(height)时间，这就是完成了哈希表不便完成的⼯作，动态性。但是⼆叉树有可能出现worst-case，如果　　　　　　　　　　　　输⼊序列已经排序，则时间复杂度为O(N)。

为什么不用二叉树来作为索引，就是因为二叉树的worst-case，如果输入序列是排好序的，那么二叉树的结构就会变成如下图所示的特殊状态：

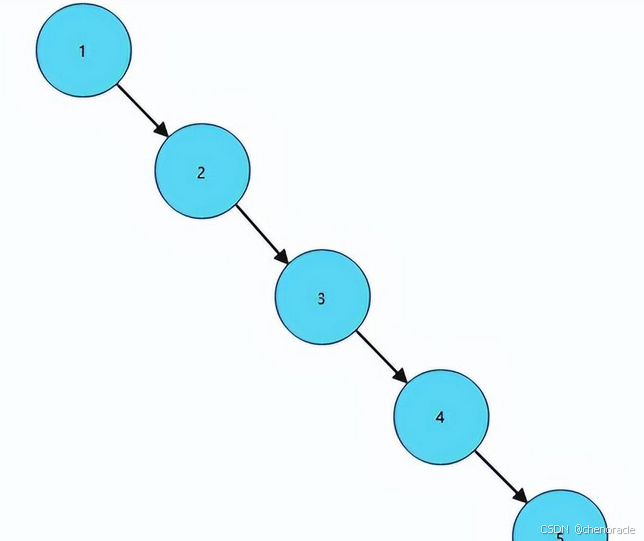
在这里插入图片描述

平衡二叉树

AVL树是严格的平衡二叉树，所有节点的左右子树高度差不能超过1；

AVL树查找、插入和删除在平均和最坏情况下都是O(lgn)。

AVL实现平衡的关键在于旋转操作：

插入和删除可能破坏二叉树的平衡，此时需要通过一次或多次树旋转来重新平衡这个树。

当插入数据时，最多只需要1次旋转(单旋转或双旋转)；

但是当删除数据时，会导致树失衡，AVL需要维护从被删除节点到根节点这条路径上所有节点的平衡，旋转的量级为O(lgn)。

由于旋转的耗时，AVL树在删除数据时效率很低；

在删除操作较多时，维护平衡所需的代价可能高于其带来的好处，因此AVL实际使用并不广泛。

红黑树:

与AVL树相比，红黑树并不追求严格的平衡，而是大致的平衡：

只是确保从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

从实现来看，红黑树最大的特点是每个节点都属于两种颜色(红色或黑色)之一，且节点颜色的划分需要满足特定的规则。

在java8中的HashMap就是使用链表+红黑树。

红黑树的缺点就是太高了，如下图所示：

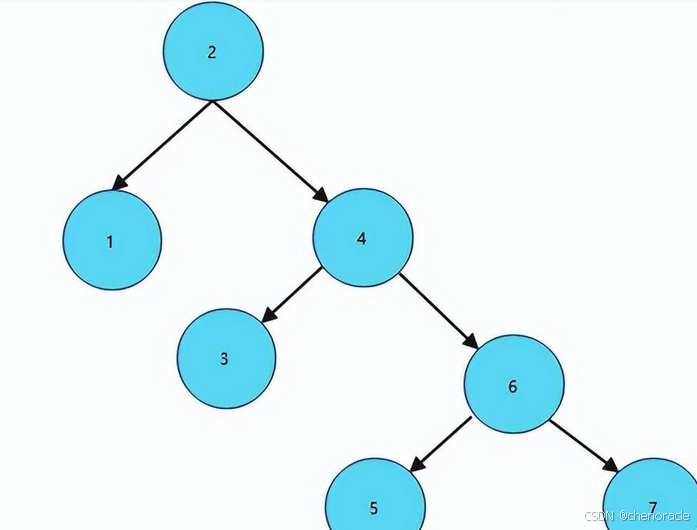
在这里插入图片描述

当数据量特别大的时候，树的高度很高，假设你要查找的节点为当前树的叶子节点，那么要查找这个节点，至少要循环h(这棵树的高度)次，所以说，红黑树在这种情况下也并不适用。

总结:

(1)B+树是数据库索引的最佳选择，尤其适合磁盘存储和大规模数据。

(2)AVL树和红黑树更适合内存中的有序数据存储，但范围查询性能较差。

(3)二叉树（BST）实现简单，但性能不稳定，适合小规模数据或临时索引。

三:详细介绍B+ Trees索引

B+树 是一种多路平衡搜索树，其设计目标是优化磁盘I/O操作，同时支持高效的范围查询。B+树的节点分为 非叶节点（内部节点） 和 叶节点，它们各自有不同的结构和规则。以下是详细介绍：

1. 非叶节点（内部节点）

结构

非叶节点存储键值（key）和指向子节点的指针。

键值用于指导搜索路径，决定下一步访问哪个子节点。

如果一个非叶节点有 n 个键值，则它有 n+1 个子节点。

规则

键值数量：

每个非叶节点最多有 m-1 个键值（m 是B+树的分支因子）。

每个非叶节点至少有 ceil(m/2) - 1 个键值（根节点除外）。

子节点数量：

每个非叶节点最多有 m 个子节点。

每个非叶节点至少有 ceil(m/2) 个子节点（根节点除外）。

键值的作用：

键值将子节点的键值范围划分开。例如，如果一个非叶节点有键值 [10, 20]，则：

第一个子节点的键值范围是 (-∞, 10)。

第二个子节点的键值范围是 [10, 20)。

第三个子节点的键值范围是 [20, +∞)。

根节点的特殊规则：

根节点可以少于 ceil(m/2) - 1 个键值，但至少要有 1 个键值（除非树为空）。

2. 叶节点

结构

叶节点存储键值和实际的数据指针（或数据本身）。

所有叶节点通过指针连接成一个有序链表，便于范围查询。

规则

键值数量：

每个叶节点最多有 m-1 个键值。

每个叶节点至少有 ceil(m/2) - 1 个键值。

数据指针：

每个键值对应一个数据指针，指向实际的数据记录（或存储数据本身）。

链表连接：

所有叶节点通过指针连接成一个有序链表，便于范围查询。

链表的顺序与键值的升序排列一致。

分裂与合并：

当叶节点满时，会分裂成两个节点，并将中间键值复制到父节点。

当叶节点的键值数量少于 ceil(m/2) - 1 时，会与兄弟节点合并。

B+树的共同规则

分支因子（Order）：

B+树的分支因子 m 决定了每个节点的最大键值数量和子节点数量。

通常，m 的值根据磁盘块大小和键值大小确定。

自平衡：

B+树通过节点的分裂与合并保持平衡。

所有叶节点位于同一层，树的高度保持平衡。

插入规则：

插入时，从根节点开始找到合适的叶节点。

如果叶节点满，则分裂叶节点，并将中间键值提升到父节点。

如果父节点也满，则递归分裂，直到根节点。

删除规则：

删除时，从根节点开始找到目标键值所在的叶节点并删除。

如果叶节点的键值数量少于 ceil(m/2) - 1，则从兄弟节点借一个键值或与兄弟节点合并。

递归调整父节点，直到根节点。

查询规则：

查询时，从根节点开始逐层向下查找，直到叶节点。

在叶节点中查找目标键值，返回对应的数据指针或数据。

总结

非叶节点 :用于指导搜索路径，存储键值和子节点指针。

叶节点 :存储实际数据，并通过链表连接支持高效的范围查询。

B+树的规则设计使其在数据库和文件系统中表现出色，尤其是在磁盘I/O优化和范围查询方面。

四:为什么有人说单表超过2000万，数据查询性能会下降？

https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

假设B+树的Degree=3(阶数)，也就是每个节点最多包含3个子个节点，那么每个节点最多可以容纳2个键值，也就是Degree-1：

在这里插入图片描述

为什么要减一？

其中:

假设，每个节点可以容纳K个键值。

对于非叶节点，如果有K个键值，那么就有K+1个指针。

例如:

K个键值分别是:1,10,20

指针就是有4个区间，而不是3个区间，所以Degree比K大1:

(1)<1

(2)大于等于1，小于10

(3)大于等于10，小于20

(4)大于等于20

下面我看看下，插入数据是，B+ Trees是如何变化的？

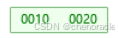
初始插入值10:

创建根节点，同时也是叶子节点。

在这里插入图片描述

然后插入键值 20，根节点的键值数量为2（未超过 M=2），直接插入。

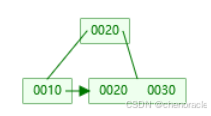
在这里插入图片描述

然后插入键值30，超过节点容量，节点进行分裂:

(1)左部分，键值10，保留在原节点中。

(2)右部分，键值20和新键值30，移动到新创建的节点中。

(3)中间键值20，会被提升到父节点(根节点)，作为分隔键。

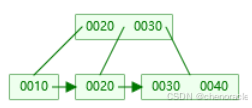
在这里插入图片描述

此时根节点的键值区间为：

第一个子节点的键值范围：(−∞,20)

第二个子节点的键值范围：[20,+∞)

然后插入键值40，插入到右叶子节点 [20, 30]，键值数量为3（超过 M=2），需要分裂:

(1)子节点左部分，键值10，保留在原节点中。

(2)子节点右部分，键值20、30中的左部分键值20保留在原节点中，右部分键值30和新键值40移动到新创建的节点中。

(3)中间键值30，会被提升到父节点(根节点)，作为分隔键。

在这里插入图片描述

然后插入键值50:

插入到右叶子节点 [30, 40]，键值数量为3（超过 M=2），需要分裂。

右叶子节点分裂为两个叶子节点：

左叶子节点：[30]

右叶子节点：[40, 50]

中间键值 40 提升到父节点（根节点）

根节点：[20, 30, 40]（键值数量为3，超过 M=2M=2），需要分裂。

根节点分裂为两个非叶子节点：

左非叶子节点：[20]

右非叶子节点：[40]

中间键值 30 提升到新的根节点。

新的根节点：[30]

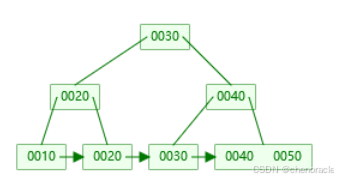
在这里插入图片描述

然后插入键值60:

插入到右叶子节点 [40, 50]，键值数量为3（超过 M=2），需要分裂。

右叶子节点[40, 50]分裂为两个叶子节点：

左叶子节点：[40]

右叶子节点：[50, 60]

中间键值 50 提升到父节点（右非叶子节点）。

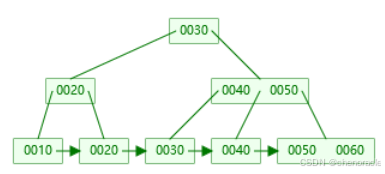
在这里插入图片描述

插入键值70:

插入到右叶子节点 [50, 60]，键值数量为3（超过 M=2），需要分裂。

右叶子节点分裂为两个叶子节点：

左叶子节点：[50]

右叶子节点：[60, 70]

中间键值 60 提升到父节点（右非叶子节点）。

右非叶子节点：[40, 50, 60]（键值数量为3，超过 M=2），需要分裂。

右非叶子节点分裂为两个非叶子节点

左非叶子节点：[40]

右非叶子节点：[60]

中间键值 50 提升到父节点（根节点）。

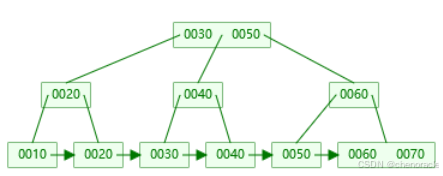
在这里插入图片描述

插入键值80:

插入到右叶子节点 [60, 70]，键值数量为3（超过 M=2），需要分裂。

右叶子节点分裂为两个叶子节点：

左叶子节点：[60]

右叶子节点：[70, 80]

中间键值 70 提升到父节点（右非叶子节点）。

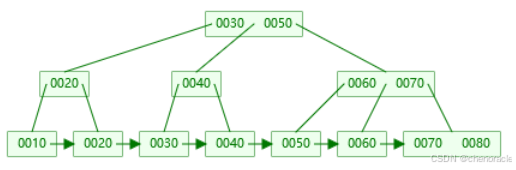
在这里插入图片描述

插入键值90：

插入到右叶子节点 [70, 80]，键值数量为3（超过 M=2），需要分裂。

右叶子节点分裂为两个叶子节点：

左叶子节点：[70]

右叶子节点：[80, 90]

中间键值 80 提升到父节点（右非叶子节点）。

右非叶子节点：[60, 70, 80]（键值数量为3，超过 M=2），需要分裂。

右非叶子节点分裂为两个非叶子节点：

左非叶子节点：[60]

右非叶子节点：[80]

中间键值 70 提升到父节点（根节点）。

根节点：[30, 50, 70]（键值数量为3，超过 M=2），需要分裂。

根节点分裂：

根节点分裂为两个非叶子节点：

左非叶子节：[30]

右非叶子节点：[70]

中间键值 50 提升到新的根节点。

新的根节点：[50]

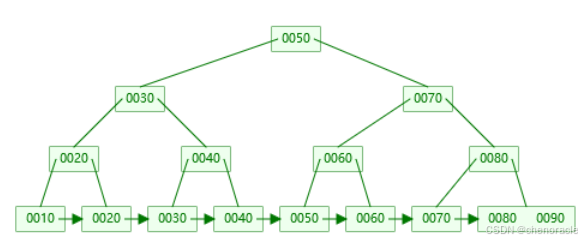
在这里插入图片描述

这时数的高度变成4，也就是level=3时，最多存8行数据。

在MySQL 数据库中，InnoDB存储引擎最小储存单元是页（Page），一个页的大小默认是16K。

B+树一个节点的大小设为1页或页的倍数最为合适。

通过下面语句可以查到，默认为16KB:

show variables like ‘innodb_page_size’;

InnoDB的B+树中:

非叶子节点:存的是键值key 加指针；

叶子节点:存的是数据行。

叶子节点:

假设一行数据大小为1k，那么一页就能存16条数据；

例如:

CREATE TABLE CJC.T1 (

id INT, -- 4 字节

big\_id BIGINT, -- 8 字节

name CHAR(10), -- 10 字节（latin1）或最多 40 字节（utf8mb4）

description VARCHAR(10) -- 实际数据长度 + 1 或 2 字节

......

);

对于非叶子节点:

如果键值key使用的是bigint类型，则为8字节，指针在mysql中为6字节，一共是14字节。

则一页16k能存放 16 * 1024 / 14 = 1170 个索引指针，每个指针对应叶子节点的一页(16KB)可以存储16条数据，也就是对于一颗高度为2的B+树，根节点存储索引指针节点，那么它有1170个叶子节点存储数据，每个叶子节点可以存储16条数据，一共 1170 x 16 = 18720 条数据。

而对于高度为3的B+树，就可以存放 1170 x 1170 x 16 = 21902400 条数据（两千多万条数据），也就是对于两千多万条的数据，我们只需要高度为3的B+树就可以完成，通过主键查询只需要3次IO操作就能查到对应数据。

按公式计算:

B+ 树的总数据量（M）与层级（L）的关系为：

在这里插入图片描述

其中：

N 是每个非叶子节点的键值数量。

L 是 B+ 树的层级。

叶子节点记录数是每个叶子节点可以存储的记录数量。

按照上面的假设:

N=1170

L=3

那么总数据量就是:2190万

(1170的2次方)*16=1170*1170*16= 21902400条数据。

同理，如果层级是4，总数据量是:256亿

1170*1170*1170*16= 25625808000

<16行，tree=1

<1170*16=18720,tree=2
<21902400,tree=3

MySQL B+tree 索引，阶数是由什么决定的？

在 MySQL 的 B+树索引 中，阶数（Order） 是一个关键参数，它决定了每个节点的 最大子节点数量 和 最大键值数量。阶数的大小直接影响 B+树的高度和查询性能。阶数主要由以下因素决定：

1. 磁盘页大小

B+树的节点通常设计为一个磁盘页的大小。

磁盘页的大小决定了每个节点可以存储的键值和指针数量。

常见的磁盘页大小为 16KB（MySQL 的默认页大小）。

2. 键值和指针的大小

键值大小：取决于索引列的数据类型。例如：

INT 类型：4 字节。

BIGINT 类型：8 字节。

VARCHAR 类型：可变长度，取决于实际存储的字符串长度。

指针大小：通常为 6 字节（指向磁盘页的地址）。

阶数的计算公式

阶数 M可以通过以下公式估算：

M=磁盘页大小/(键值大小+指针大小)

示例

假设：

磁盘页大小：16KB（16384 字节）。

键值大小：8 字节（BIGINT 类型）。

指针大小：6 字节。

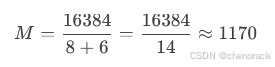
在这里插入图片描述

这意味着：

每个节点最多可以有 1170 个子节点。

每个节点最多可以存储 1169 个键值。

五:B+ Trees索引为什么对’%xxx%'类型模糊查询不起作用?

B+树索引 对模糊查询（如 LIKE ‘%abc%’ 或 LIKE ‘abc%’）的支持有限，主要原因在于B+树的结构和设计目标。以下是详细分析:

B+树索引的工作原理

B+树是一种有序数据结构，所有键值按升序排列。

查询时，B+树通过逐层比较键值，快速定位目标数据。

对于精确匹配查询（如 =）和前缀匹配查询（如 LIKE ‘abc%’），B+树可以高效工作。

2. 模糊查询的类型

模糊查询通常分为两种：

前缀匹配（如 LIKE ‘abc%’）：

查询以 abc 开头的字符串。

B+树可以支持这种查询，因为键值是有序的，可以通过范围查询快速定位。

通配符匹配（如 LIKE ‘%abc%’ 或 LIKE ‘%abc’）：

查询包含 abc 或以 abc 结尾的字符串。

B+树无法直接支持这种查询。B+树无法利用键值的有序性进行快速定位。

无法跳过前缀

B+树的查询是从根节点开始，逐层比较键值的前缀。

对于 LIKE ‘%abc%’，查询需要跳过任意长度的前缀，B+树无法高效处理。

六:MySQL和Oracle的B+ tree索引有什么不同？

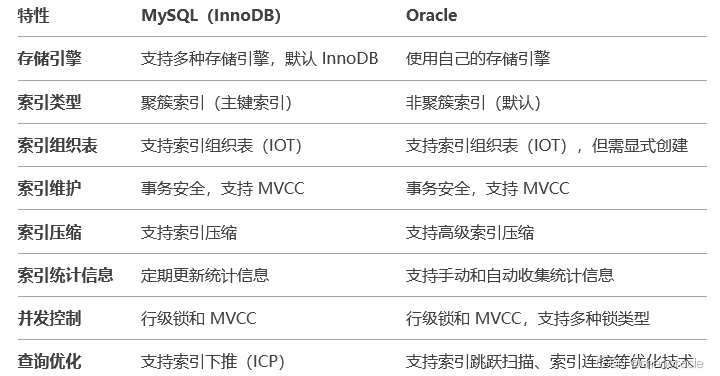
在这里插入图片描述

MySQL（InnoDB）：

InnoDB 使用聚簇索引，即主键索引的叶子节点存储完整的数据行。

如果没有显式定义主键，InnoDB 会自动生成一个隐藏的主键（6字节）。

隐藏主键是一个 6 字节的整数，由 InnoDB 自动生成。

它用于唯一标识表中的每一行数据。

隐藏主键的值是全局唯一的，即使在同一张表中也不会重复。

隐藏主键是 InnoDB 内部使用的，默认情况下不会暴露给用户。但可以通过以下方式间接查询：

在 MySQL 中，可以使用 _rowid 伪列来查看隐藏主键的值。

SELECT _rowid, * FROM your_table;

可以通过 INFORMATION_SCHEMA.COLUMNS 查看表的列信息，但隐藏主键不会直接显示。

隐藏主键的作用:

唯一标识行：

隐藏主键用于唯一标识表中的每一行数据，确保每行数据都有一个唯一的标识符。

支持索引组织表：

InnoDB 的表是索引组织表（IOT），数据按照主键索引的顺序存储。

如果没有显式定义主键，隐藏主键会作为主键索引的键值。

支持二级索引：

InnoDB 的二级索引存储的是主键值。如果没有显式定义主键，二级索引会存储隐藏主键的值。

隐藏主键对查询性能的影响

查询性能：

隐藏主键本身不会显著提高查询性能。

如果表没有显式定义主键，查询时可能需要扫描更多的数据，因为隐藏主键的值是随机的，无法利用有序性加速查询。

隐藏主键对主从同步的影响

主从同步：

隐藏主键不会显著提高主从同步的速度。

七:MySQL和达梦数据库索引组织表的区别

MySQL和达梦数据库默认表都是索引组织表，B+ tree索引有什么不同，为什么不显示创建主键情况下，达梦比MySQL查询性能好？

MySQL数据库:

隐藏主键是随机的，可能导致数据插入时产生更多的页分裂和碎片化，影响查询性能。

达梦数据库:

如果没有显式定义主键，达梦数据库会自动生成一个隐藏的主键，但其实现方式可能更高效。

达梦数据库的隐藏主键可能具有更好的顺序性，减少了页分裂和碎片化。

参考:


1.https://www.deepseek.com/

2.[https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html](https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html)

3.https://zhuanlan.zhihu.com/p/562512587

**重要消息: **

近期发布了达梦数据库实战课程，预计30课时左右，当前已经发布了8课时，主要以实战运维为主，感兴趣的朋友可以订阅，一起学习！
https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzI5OTY2NzQ5MA==&action=getalbum&album_id=3846239617787428865&scene=21#wechat_redirect
图片.png