01-复杂度3 二分查找 (20 分)

题目

本题要求实现二分查找算法。

函数接口定义：

Position BinarySearch( List L, ElementType X );

其中List结构定义如下：

typedef int Position;
typedef struct LNode *List;
struct LNode {
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
};

L是用户传入的一个线性表，其中ElementType元素可以通过>、==、<进行比较，并且题目保证传入的数据是递增有序的。函数BinarySearch要查找X在Data中的位置，即数组下标（注意：元素从下标1开始存储）。找到则返回下标，否则返回一个特殊的失败标记NotFound。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 10
#define NotFound 0
typedef int ElementType;

typedef int Position;
typedef struct LNode *List;
struct LNode {
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
};

List ReadInput(); /* 裁判实现，细节不表。元素从下标1开始存储 */
Position BinarySearch( List L, ElementType X );

int main()
{
    List L;
    ElementType X;
    Position P;

    L = ReadInput();
    scanf("%d", &X);
    P = BinarySearch( L, X );
    printf("%d\n", P);

    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例1：

5
12 31 55 89 101
31

输出样例1：

2

输入样例2：

3
26 78 233
31

输出样例2：

0

鸣谢宁波大学 Eyre-lemon-郎俊杰 同学修正原题！

代码

int BinarySearch( List L, ElementType X )
{
ElementType max = L->Last;
ElementType min =1;
ElementType judgenum = 1;
while(max>=min)
{
    judgenum = (max - min)/2 + min; //防止数值溢出
    if(L->Data[judgenum]<X)
        {
            min = judgenum+1;
        }   
    else if(L->Data[judgenum]>X)
        {
            max = judgenum-1;
        }
    else if(L->Data[judgenum]==X)
        {
            return judgenum;
        }
    
}
return NotFound;
}

2020再次做题，发现。

Position BinarySearch( List L, ElementType X ){


    Position lastelement = L->Last;
    Position firstelement= 1;       //操作对象是下标9New0
    Position binary = 1;

    while(lastelement >= firstelement){         //加=（new）

        binary = (lastelement - firstelement)/2 + firstelement;
		//binary = (lastelement + firstelement)/2 ;亦可

        if (L->Data[binary] < X){
            firstelement = binary + 1;  //  （+1）
        }
        else if(L->Data[binary] > X){
            lastelement = binary - 1;
        }
        else if(L->Data[binary] == X){  //(-1)
            return binary;
        }
    }

    return NotFound;



}

二分查找的核心首先确定 输入字符串的首尾位置，每次循环求一次中值位置。当找到值时就返回，未找到返回NotFound

操作线性表时，通过操作数组下标来进行表的增删改查。

防止L+F溢出int的具体操作。推荐使用
binary = (lastelement - firstelement)/2 + firstelement;

瞎抄的

概念： 二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好，占用系统内存较少;其缺点是要求待查表为有序表，且插入删除困难。

只是最普通的二分，实际上，二分还可以实现非等值查找，例如平时所说的二分求上界，二分求下界之类的。

二分的更深入抄袭

bool bFind(int a[],int left,int right,int tag)
{
		for( ;left<=right;)
		{
				int mid = (left + right)>>1;
				if(a[mid]==tag)
					return tag;
				else
					a[mid]<tag ? l=mid + 1 : r = mid -1;
		}
		return false;
}

这就是最简单的二分了，我们来具体看看它的计算过程

首先该写法它的 l 和 r，即我们二分的区间的左右端点，它是保证要找的数在[l, r)里的，也就是区间左端点可能是我们要找的数，而区间右端点不可能是

当区间中点mid偏小时，l = mid + 1，二分区间变成[mid + 1, r)，如果该数字存在，必定还在该区间内；

如果mid偏大，r = mid，mid不可能是我们要找的数，而r端点本来就不会是答案，所以可以这么写

所以每次二分区间[l, r)，区间必定会缩小，不可能死循环，最后一次判定时（如果一直没找到该数），区间变成[l, l + 1)，这时候mid = l，如果mid还不等于我们要找的数，区间就会缩小到 l == r ，便退出了循环，返回-1表示没找到

虽然该写法没什么大问题，而且比较简洁，但是我们需要注意：

mid = (l + r) / 2 ，l + r可能会超过int范围，我们也可以写成 l + (r - l) / 2，可以了防止溢出，并且具有更好的通用性(如果 l 和 r 是迭代器或者指针，第一种就不行了, 因为迭代器或指针是不能相加的)

二分法求上下界

链接

官方标准，位运算

public static int binary(int[] arr, int data) {
        int min = 0;
        int max = arr.length - 1;
        int mid;
        while (min <= max) {
            // 无符号位运算符的优先级较低，先括起来
            mid =  min + ((max - min) >>> 1);
            if (arr[mid] > data) {
                max = mid - 1;
            } else if (arr[mid] < data) {
                min = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }

作者：程序员吴师兄
链接：https://zhuanlan.zhihu.com/p/64286137
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

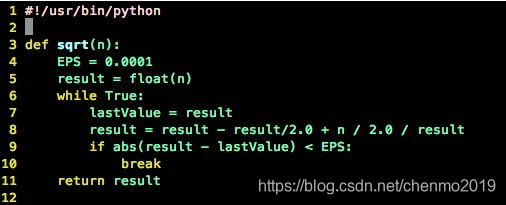
牛顿法-开根号程序