基于kbqa 的复旦大学论文解释 learning question answering over QA corpora and knowledge bases(二)

我们表示第i项其中,,所以,所以我们建立了QA与X的似然线性关系，

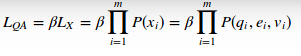                                                                                   (13)

最大似然估计QA就是等价最大似然估计X，（2）通过边际化联合概率,得到,基于总体的模板t和谓语p，似然如公式（14），我们阐述整个过程如图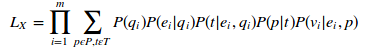4，                                                             (14)

可以说公式14是整个论文核心我们只要计算每一个分量。让整个似然概率最大化，这就是整个论文的目标。

4.2   Parameter Estimation

         目标：在这一章我们评估，通过最大化公式14，我们把分布作为参数，它对应的似然估计为，把作为因此我们有评估的如下：

                                                         (15)           

其中            

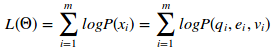
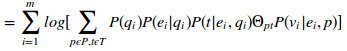                                           (16)

Intuition of EM Estimation:    我们注意到一些变量，例如谓语predicate和tenmplates在构建的模型中是隐变量，因此促使我们使用EM算法来评估参数，EM算法是寻找参数的最大似然估计的经典方法，在统计模型中，并且适用于不可观测变量。我们最后的目标就是最大似然完整的数据，由于涉及到求和以及计算的复杂性，因此我们利用他的下界【7】，这里不再赘述由于时间因素，感兴趣可以去看这篇文献，例如Q-function。为了定义Q-function，我利用完整数据的似然估计，EM算法通过迭代最大化的下界，在第s步迭代，

zaiE-STEP对于给定的参数，计算，在M-STEP。评估参数（在下一次的迭代参数），这个参数是的最大化下界。

         Likelihood of Complete Data: 直接的最大化计算比较复杂，由于具有求和操作，如果我们知道每一个可观测的数据的完整数据，例如知道template和predicate，则估计变得容易了，因此我们队每一个可观察的三元组引入一个隐变量，隐变量是predicate和template对例如,预示这是由predicate和template共同产生，之所以把他两个放在一起，是由于他们之间不是相互独立的，因此,,使用谓语以及模板生成这个概率，

          用,Z和X构成一个完整的数据，可观察的完整数据似然估计如下

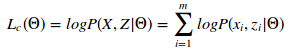                               ：                                                  (17)

其中

                                                                         (18)

                                                                     (19)

正如在3,2章讲的，f()可以在评估P(p|t)之前单独计算，所以我们可以把他当做已知的因子。

        Q-function：替代直接优化,而是定义一个Q-function在等式（20），是全部观察数据似然的期望，因此是第s步的估计，根据理论1当把作为一个常数，为提供一个下界，所以我们尝试优化。

      

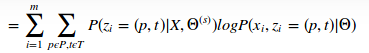                                                                       (20)

仔细去理解这一个，基于问题，实体以及value下的，并且已知的条件下的，谓语p与模板t同时发生的条件概率，数据实话，这个概率的构造我也是一直没明白其中的原理，还需要作者去说明构造的原理何在。但是我猜想，回顾上边的一句话，直觉上，如果我们知道每一个观测数据的完整的三元组（q,e,v），并且由三元组所产生的t和p,估计变得容易，当然了，应为t和p都知道了，条件概率自然就知道了，但是不知道理解的是否有误，（所以作者引入隐变量z=（p，t）），但是作者这句话有待考究，is the probability that x i is generated    with predicate p and template t.在google翻译为是由t和p,

p是x产生的概率使用谓词P和模板T。正确理解应该是p是x使用p和t产生的概率。

 

但是对比公式（20）和公式（17）会发现仅仅多个概率公式，一定是

       作者定义了一个原理（下界文献【10】）

其中仅仅依赖与在中可以视为一个常数。假设在作者的解析下以上我们都能够理解下界是怎么构造的（当然，我是不懂怎么构造的）。

以上是我对作者构造下界的粗俗理解，至于是否有客观的理论，有待考究，反正就是多了一个条件概率。

但是并不影响实现最后的结果，

  In E-step, 我们计算我么计算公式（20）中的每一个

                                                  (21)

              相当于已知参数，求这个概率的期望值

In M-step, 最大化Q-function ，用的则是拉格朗日来获取:

           

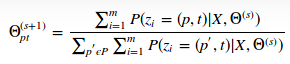
 这个概率有点像softmax，其实就是对于当前实际pt这样的概率进行归一化更新。具体算法说明白的比较清楚，在4.3章将会有比较详细的解释。

    4.3 Implementation   

        首先进行初始化，为了避免变为0，需要对于所有的是一个均匀分布，使得，主要是看公式23怎么解释，是关键。这个也影响我好长时间，

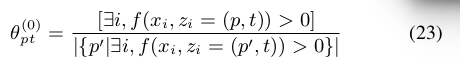
分子是存在i 使得，重点大概意思就是一定存在问题，一个实体对应的谓语对应这个概念，也就是模板，模板可能对应多个问题数据，但是一定存在，分母理解最重要，刚才看了一下自己实现的代码，想起来了，怎么会出现一个问题对应多个谓语呢，不管这些，作者的意思英嘎就是同一个templates可能对应多个谓语，由于是上万训练数据集，所以可能是的，有什么理解错的，请指正，具体请看我实现的代码。

E-step: 我们枚举所有的数据集通过公式（21）来计算，计算复杂度为，

      以下仅为个人理解，根据我的代码在理解一边，由于长时间忘记了，复杂度为m，比较容易理解，因为有m个数据集，每一个数据集计算 ，我们已经初始化了参数，所以对于公式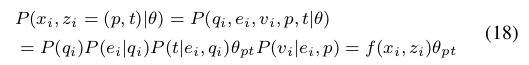

来计算并不太难，因为我们可以计算出来，由于根据章节3.2，以及初始化参数，的每一个参数都是常量。

M-step: 对于每一个，我们计算，由于我们需要枚举所有的tempaltes和predicates，所以计算复杂度为，下一步，我们直接枚举常数项的templates和predicates对于每一个样本，所以时间复杂度减小到。

       注意到仅仅是的的三元组才需要考虑，由于公式18 和19 意味着：

 

就可以删减枚举的模板，意味着我们仅仅枚举通过概念化问题中q i的实体e i得到的templates，由于实体e i的对应概念是整个概率的上界，很明显可以被考虑一个常数，意味着仅仅谓语predicate连接了和，其实，在知识库中，一旦实体和谓语确定，基本value已经确定，所以以上基本上是废话。

再把伪代码跌上来，基本上就完成了自己的代码实现与论文对应的关系。以后的章节，由于自己觉着不靠谱。并且没有太大技术含量，没有用到深度学习任何模型，并且使用性不是太强，接下来将结合代码讲解伪代码。