布雷斯悖论 nash平衡点

最新推荐文章于 2025-09-04 13:13:29 发布

转载最新推荐文章于 2025-09-04 13:13:29 发布 · 1.6k 阅读

文章标签：

#交通

算法理论专栏收录该内容

7 篇文章

订阅专栏

本文探讨了交通网络中的Braess悖论，解释了为何增加一条近路反而可能使整体通行时间增加的现象，并引入纳什均衡概念来理解个体与集体利益之间的矛盾。

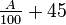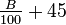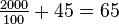考虑右图中的交通网，有4000辆车打算在其中路上通行。通过的时间从起点到A是路上车的数量除以100，而从起点到B是固定的45分钟(另一条路相同)。如果近路不存在(即交通网上只有4条路)，从起点到A到终点需要的时间是 $\tfrac{A}{100} + 45$ ，而从起点到B到终点需要的时间是 $\tfrac{B}{100} + 45$ 。如果其中某条路的通过时间更短，是不可以达到纳什均衡的，因为任何一个理性的司机都会选择更短的路。因为有4000辆车，易知 $A + B = 4000$ 可以解得 $A = B = 2000$ 这样每条路的通过时间都是 $\tfrac{2000}{100} + 45 = 65$ 分钟。

现在假设有了一条近路(通过时间接近于0)，在这种情况下所有的司机都会选择从起点到A到B这条线路，因为就算所有的车都走这条路，通过时间也不过40分钟，小于起点到B的45分钟。到达A之后，所有的司机都会选择从用接近0的时间行驶到到B再到终点，因为就算所有的车都走这条路，通过时间也不过40分钟，小于A到终点的45分钟。这样所有车的通过时间是 $\tfrac{4000}{100} + \tfrac{4000}{100} = 80$ 分钟，比不存在近道的时候还多了15分钟。因为没有司机愿意切换到别的路上去，所以走原先的路线(起点A终点，起点B终点)的时间都变成了85分钟。如果大家都约定好不走近路，那么都可以节约15分钟的时间。但是，由于单个的司机总是能从抄近道上获益，所以这种约定是不稳定的，于是Braess悖论便出现了。

很有意思诶~~~所以去掉A->B反而提高了时间。。。个体利益与整体利益不一致。。。

nash平衡点（博弈论经典问题，好像就是《美丽心灵中》的nash）

其经典的例子就是囚徒困境。囚徒困境是一个非零和博弈。大意是：一个案子的两个嫌疑犯被分开审讯，警官分别告诉两个囚犯，如果你招供，而对方不招供，则你将被立即释放，而对方将被判刑十年；如果两人均招供，将均被判刑两年。如果两人均不招供，将最有利，只被判刑半年。于是，两人同时陷入招供还是不招供的两难处境。但两人无法沟通，于是从各自的利益角度出发，都依据各自的理性而选择了招供，这种情况就称为纳氏均衡点。这时，个体的理性利益选择是与整体的理性利益选择不一致的。

囚犯甲的博弈矩阵		囚犯甲
囚犯甲的博弈矩阵		招供	不招供
囚犯乙	招供	各判刑两年	甲判刑十年,乙立即释放
囚犯乙	不招供	甲立即释放,乙判刑十年	各判刑半年

基于经济学中“理性经济人”的前提假设，两个囚犯符合自己利益的选择是坦白招供，原本对双方都有利的策略不招供从而均被判刑半年就不会出现。事实上，这样两人都选择坦白的策略以及因此被判两年的结局被称作是“纳什均衡”（也叫非合作均衡），换言之，在此情况下，无一参与者可以“独自行动”（即单方面改变决定）而增加收获。。

你的利益受到他人限制了。。。

什么时候达到nash平衡

甲选择方案1 ，乙为了自己利益最大化选择方案2.。。。若乙先选择方案2，甲为了达到自己利益最大化选择方案1.。。则达到了一个nash平衡点。。

相反，若

甲先选方案1，乙选方案2 。

乙先选方案2 ，甲会选方案3 。

甲选择方案3，乙选择方案1 。

乙选择方案1，甲选择方案1 。循环开始，无休止。。。