1. 前言
- 来自广工考研真题
- 题目是Top K问题的一类
- 后文将阐释这一题所产生的思考
2. 题目
假设二叉排序树中增设一个lsize域,其值为该结点的左子树中的节点数加1。其类型定义如下:
typedef struct BiTNode {
char data; // 题中没有读写这个数据,可以忽略
int lsize;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
算法f5求二叉排序树中第k小的结点的位置。
3. 思路
3.1 用什么遍历方式
- 先序遍历
查找元素,找到后直接返回即可,没找到依次向左子树右子树找。找到元素后,直接返回,不需要延迟处理(中序、后序都支持第二次访问再处理),优先用先序遍历做。
3.2 找规律
-
将元素的lsize填上
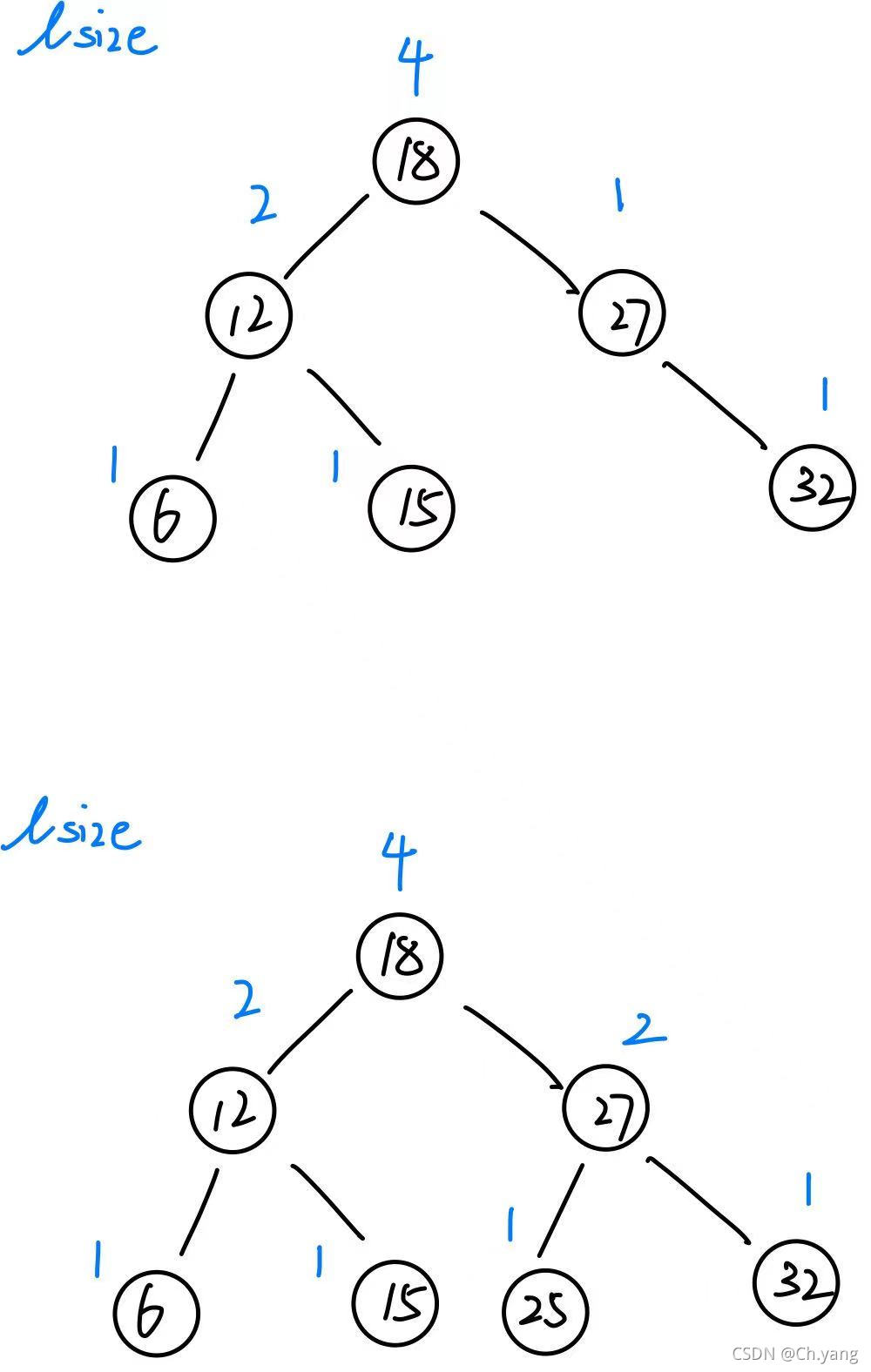
-
扮演左孩子角色的节点 lsize == 自身在数据集合中的倒序排名
-
(扮演右孩子角色的节点 lsize + 双亲节点的 lsize) == 自身在数据集合中的倒序排名
3.3 画图验证
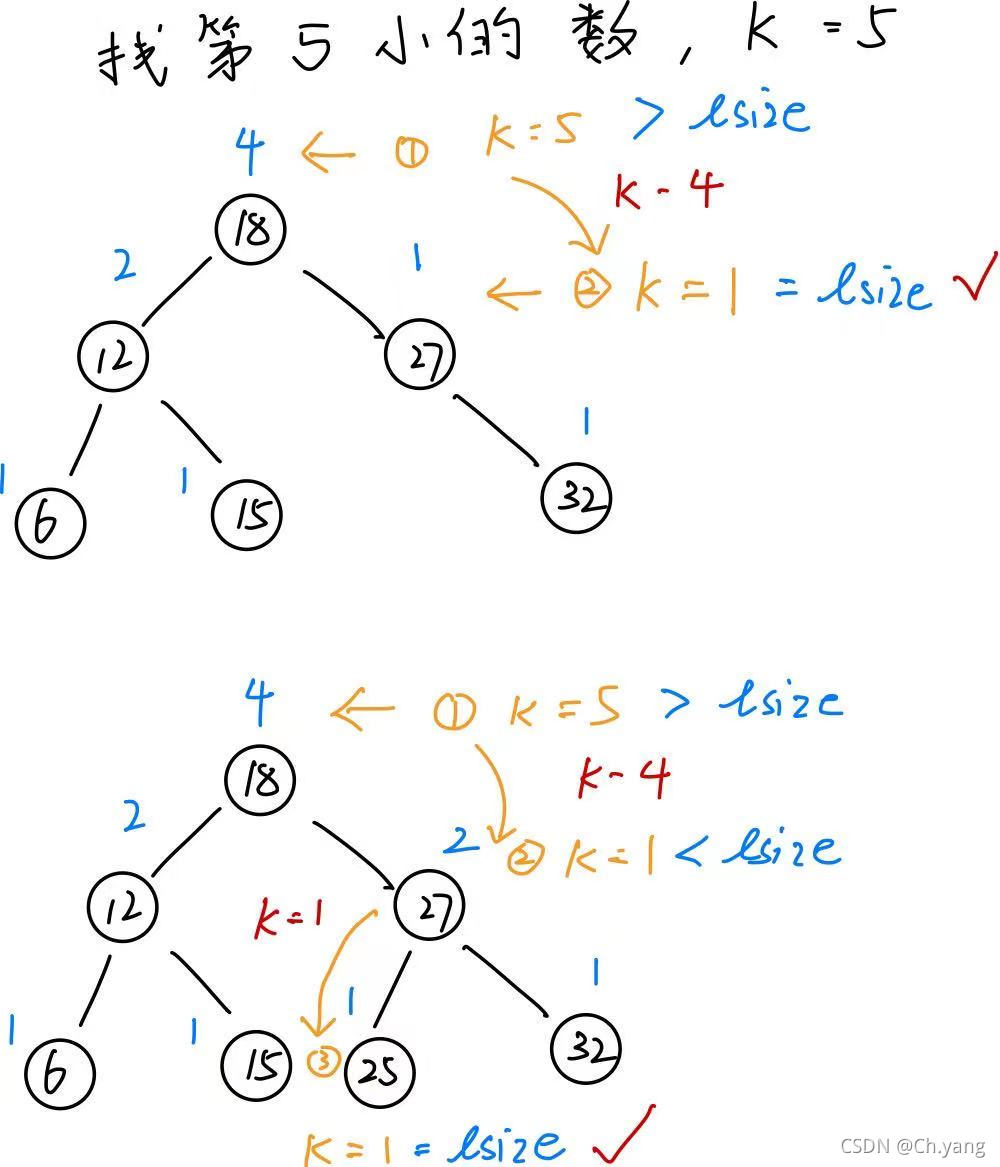
4. 题解
BiTree f5(BiTree T, int k) {
if (NULL == T) return NULL;
if (T -> lsize == k) {
return T;
} else if (T -> lsize > k) {
return f5(T -> lchild, k);
} else {
//(扮演右孩子角色的节点 lsize + 双亲节点的 lsize) == 自身在数据集合中的倒序排名
// => 扮演右孩子角色的节点 lsize == 自身在数据集合中的倒序排名 - 双亲节点的 lsize
int actualK = k - T-> lsize;
return f5(T -> rchild, actualK);
}
}
5. 后记
- 实际应用中,可以使用后序遍历对lsize进行初始化,后序遍历基础相关的题
再使用先序遍历的思想做元素的搜索,就TopK 问题。搜索的时间复杂度都是O(logn) - 强化二叉排序树的性质
元素的键值大于其左子树,及双亲节点、双亲节点的左子树
如图 27 > 25 > 18 > …
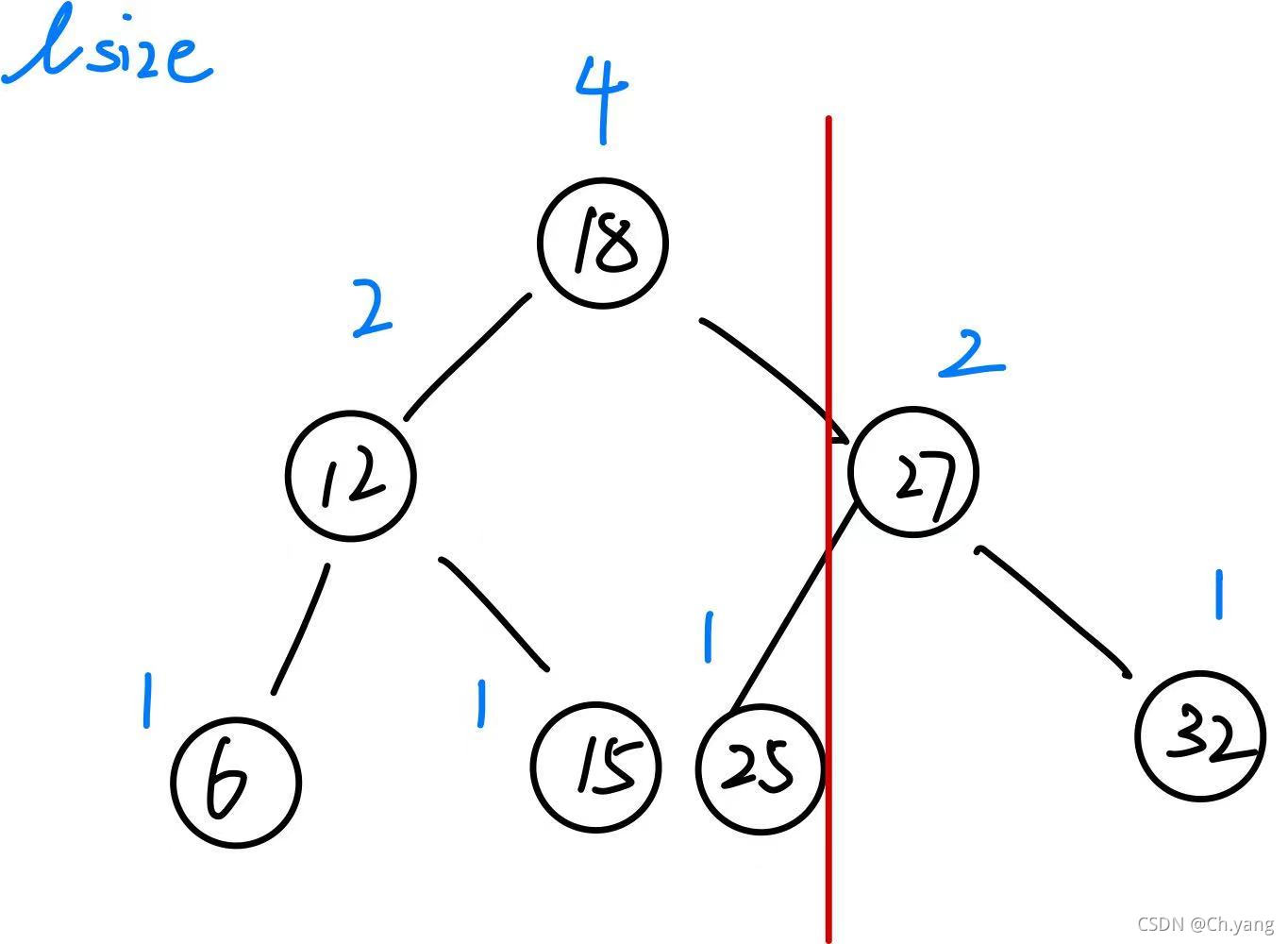








 本文探讨了一种基于二叉排序树的TopK问题解决方案,通过增设节点的lsize域来辅助查找。首先,介绍了利用先序遍历寻找第k小元素的思路,其次,阐述了lsize域的填充分析,以及如何利用lsize的规律进行查找。最后,给出了算法f5的实现,并指出搜索时间复杂度为O(logn)。该方法强化了二叉排序树的性质,适用于数据集中的快速查找操作。
本文探讨了一种基于二叉排序树的TopK问题解决方案,通过增设节点的lsize域来辅助查找。首先,介绍了利用先序遍历寻找第k小元素的思路,其次,阐述了lsize域的填充分析,以及如何利用lsize的规律进行查找。最后,给出了算法f5的实现,并指出搜索时间复杂度为O(logn)。该方法强化了二叉排序树的性质,适用于数据集中的快速查找操作。
















 2069
2069

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








