【剑指 Offer 59 - I. 滑动窗口的最大值】（优先队列）

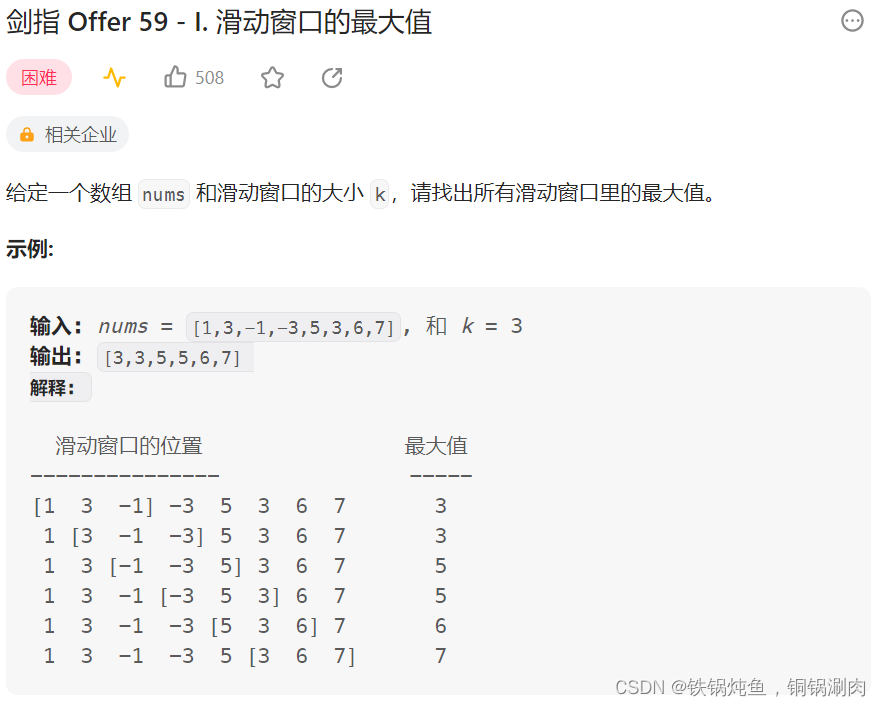
【解题思路】

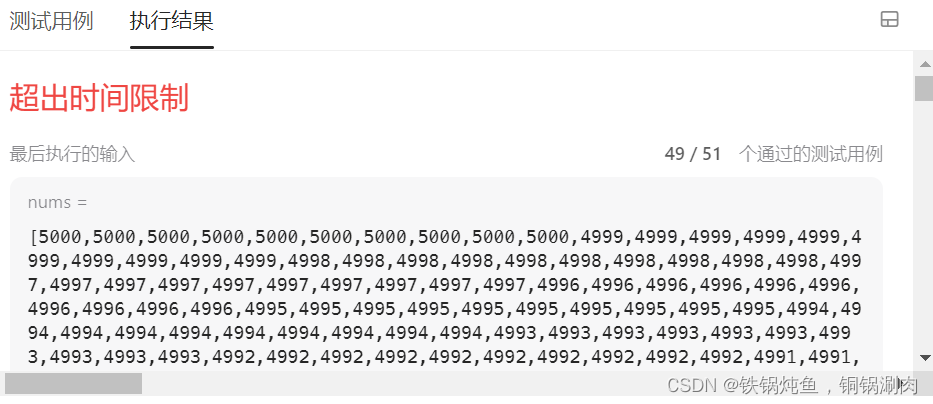
暴力法，超出时间限制。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length - k + 1;
        int[] ans = new int[n];
        int max = -99999;

        for(int i = 0; i < k; i++)
        {
            if(nums[i] > max)
            {
                max = nums[i];
            }
        }
        ans[0] = max;

        for(int i = k; i < nums.length; i++)
        {
            if(nums[i] > ans[i-k])
            {
                ans[i-k+1] = nums[i];
            }
            else if(ans[i-k] != nums[i-k])
            {
                ans[i-k+1] = ans[i-k];
            }
            else{
                max = -99999;
                for(int j = i; j > i-k; j--)
                {
                    if(nums[j] > max)
                    {
                        max = nums[j];
                    }
                }
                ans[i-k+1] = max;
            }
        }
        return ans;
    }
}

 

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] pair1, int[] pair2) {
                return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
            }
        });
        for (int i = 0; i < k; ++i) {
            pq.offer(new int[]{nums[i], i});
        }
        int[] ans = new int[n - k + 1];
        ans[0] = pq.peek()[0];
        for (int i = k; i < n; ++i) {
            pq.offer(new int[]{nums[i], i});
            while (pq.peek()[1] <= i - k) {
                pq.poll();
            }
            ans[i - k + 1] = pq.peek()[0];
        }
        return ans;
    }
}