7-3 DAG图优化 (15 分)

最新推荐文章于 2025-12-02 09:58:47 发布

原创最新推荐文章于 2025-12-02 09:58:47 发布 · 2.5k 阅读

16 ·

CC 4.0 BY-SA版权

编译原理专栏收录该内容

32 篇文章

订阅专栏

本文介绍了一种基于DAG图的代码优化方法，通过构造DAG图并进行代码优化，可以有效减少冗余变量，提高代码效率。文章提供了一个具体的实现示例，包括输入输出格式和C++代码实现。

7-3 DAG图优化 (15 分)

大家都学过了代码优化，其中有一个DAG优化，这次我们就练习这个操作。

输入格式:

输入第一行为一个整数ｎ(n < 100)，表示该组输入的表达式的个数。

之后ｎ行为表达式，每个变量为一个字母，表达式仅包括二元运算 + - * / 。

例如：A=B+C 。

输出格式:

通过构造DAG图，进行代码优化，只需要保留AB，删除无用变量，删除变量时，尽量保留最早出现的变量。

PS:保证AB的值不同

输入样例:

3
A=B+C
B=B+B
A=C+C

输出样例:

B=B+B
A=C+C

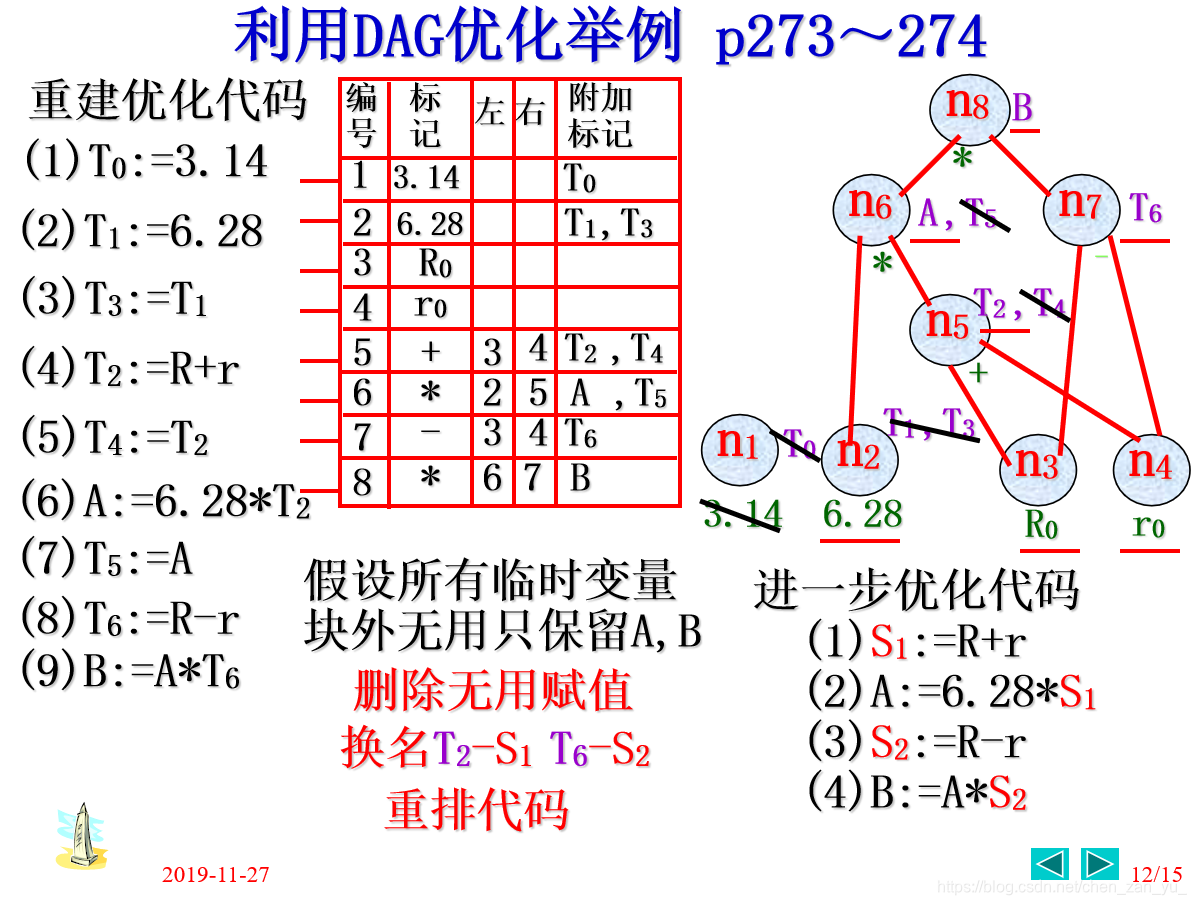
可以根据这个图中的树来理解下面的代码流程 over~~

#include <bits/stdc++.h>
using namespace std;
int n;
int cnt;
char s[10];
char ans[101][101];
bool flas[101];
struct st
{
    char id;///存放每个结点的的值
    int left=-1;///左右子树初始化为-1
    int right=-1;
    vector<char>var;///存放每个表达式的根节点
} node[101];
bool find_var(int i,char c)///查看这个数是否出现在更结点中
{
    int len=node[i].var.size();
    for(int k=0; k<len; k++)
    {
        if(node[i].var[k]==c)
        {
            return true;
        }
    }
    return false;
}
int add_node(char c)///若结点不存在就增加结点
{
    for(int i=cnt-1; i>=0; i--)
    {
        if(node[i].id==c||find_var(i,c))
        {
            return i;
        }
    }
    node[cnt].id=c;///若不存在，则加入新的结点
    return cnt++;
}
void add_operator(char c,char op,int l,int r)///存放整条操作数
{
    for(int i=cnt-1; i>=0; i--)///若运算符，左右结点都存在，则只要加入根节点
    {
        if(op==node[i].id&&node[i].left==l&&node[i].right==r)
        {
            node[i].var.push_back(c);
            return;
        }
    }
    node[cnt].id=op;///若都不存在，则都加入
    node[cnt].left=l;
    node[cnt].right=r;
    node[cnt].var.push_back(c);
    cnt++;
}
void dfs(int x)
{
    if(node[x].left!=-1)///若存在左子树，就DFS
    {
        flas[x]=1;
        dfs(node[x].left);
        dfs(node[x].right);
    }
}
int main()
{
    cnt=0;
    scanf("%d",&n);
    for(int i=0; i<n; i++)
    {
        scanf("%s",s);
        int l=add_node(s[2]);
        int r=add_node(s[4]);
        add_operator(s[0],s[3],l,r);
    }
    for(int i=0; i<cnt; i++)
    {
        if(node[i].left!=-1)///判断，如果一个结点存在左子树，则把这个结点和左右子树都保存下来，也就是保存这条表达式
        {
            ans[i][0]=node[i].var[0];
            ans[i][1]='=';
            st ll=node[node[i].left];
            st rr=node[node[i].right];
            ans[i][2]=ll.var.size()>0?ll.var[0]:ll.id;///如果左子树也是个根结点，就加入他第一次存入的那个根结点，否则直接加入他的值
            ans[i][3]=node[i].id;
            ans[i][4]=rr.var.size()>0?rr.var[0]:rr.id;
            ans[i][5]=0;
        }
    }
    for(int i=cnt-1; i>=0; i--)
    {
        if(ans[i][0]=='A')///从后往前遍历，遇到根结点是A的就进入DFS
        {
            dfs(i);
            break;
        }
    }
    for(int i=cnt-1; i>=0; i--)
    {
        if(ans[i][0]=='B')///从后往前遍历，遇到根结点是B的就进入DFS
        {
            dfs(i);
            break;
        }
    }
    for(int i=0; i<cnt; i++)
    {
        if(flas[i])///输出DFS后保留下来的表达式
        {
            puts(ans[i]);
        }
    }

    return 0;
}