[Data Structure-Binary Tree]二叉树的概念及其扩展

数据结构 - 二叉树

二叉树(Binary Tree)

基本概念

树的概念¹

• 自然递归定义：一棵树是一些节点的集合。这个集合可以为空集；若非空，则一棵树由称作根(root)的节点r及0个或多个非空子树 T₁，T₂，… ，T_k 组成，这些子树中每一颗的根都被来自根r的一条有向边(edge)连接。

• 每一颗子树的根叫做根r的儿子(子节点，child)；r是每一颗子树的根的父亲(父节点，parent)。类似方法定义祖父(grandparent)和孙子(grandchild)关系。
• 从递归定义中我们发现，一棵树是N个节点和N - 1条边的集合，其中一个节点叫做根。

• 存在N - 1条边的结论推导：每条边都将某个节点连接到他的父节点，而除去根节点外每一个节点都有一个父节点。

• 从节点 n₁ 到 n_k 的路径(path)定义为节点n₁，… ，n_k的一个序列，使得对于1 <= i < k，节点 n_i 是节点 n_i+1 的父亲。路径的长(length)为该路径中边的条数，为 k - 1。
• 对任意节点 n_i ，其深度(depth)定义为从根到 n_i 的唯一路径的长。
• n_i的高(height)定义为：n_i 到一片树叶的最长路径的长。
  一棵树的深度等于它最深的树叶的深度；该深度总是等于这棵树的高。

• 森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

---

二叉树的概念

• 二叉树是一棵树，其中每个节点都不能多于两个儿子
• 平均二叉树的深度要比N小得多

二叉树的定义

• 每个节点都是一个结构体，其中包括关键字(value)和指向左儿子(left_child)与右儿子(right_child)的指针

typedef struct TreeNode {
	int value;
	struct TreeNode *left;//左子节点
	struct TreeNode *right;//右子节点
	TreeNode(int value) {
		this->value = value;
		this->left = this->right = NULL;
	}
}BiNode, *BiTree;

二叉树的操作

函数声明

#ifndef UNIX
#define SUCCESS 1;
#define FAILURE 0;
#else
#define SUCCESS 0;
#define FAILURE 1;
#define ERROR_CODE_X X;
#endif // !UNIX

#ifndef BinaryTree_H
struct TreeNode;
typedef struct TreeNode BiNode;
typedef struct TreeNode *BiTree;

int CreateBiTree(BiNode  **root);
void PreOrderBiTree(BiTree root);
void PreOrderBiTreeByStack(BiTree root);
void InOrderBiTree(BiTree root);
void InOrderBiTreeByStack(BiTree root);
void PostOrderBiTree(BiTree root);
void PostOrderBiTreeByStack(BiTree root);
void levelOrderBiTree(BiTree root);

int MaxDepthOfBiTree(BiTree root);
int SumOfLeaveNode(BiTree root);
BiTree CreateBiTreeByPreAndIn(int *inOrder, int *preOrder, int length);
BiTree CreateBiTreeByPostAndIn(int *inOrder, int *postOrder, int length);

void InOrderBiTreeByMorris(BiTree root);
void PreOrderBiTreeByMorris(BiTree root);
void reverse(BiTree p1, BiTree p2);
void printReverse(BiTree p1, BiTree p2);
void PostOrderBiTreeByMorris(BiTree root);

#endif // !BinaryTree_H

初始化

• 递归初始化二叉树，参数为每颗子树的根节点的二级指针

int CreateBiTree(BiNode **root) {
	//**root为二级指针,指向根节点的指针(根节点的地址值)存放的地址
	int value;
	printf("请输入该节点的值:\n");
	scanf_s("%d", &value);
	if (value <= 0) {
		//设二叉树的节点关键字(int)只能大于0
		*root = NULL;
		return FAILURE;
	}

	*root = (BiTree)malloc(sizeof(BiNode));
	if (!root) {
		printf("为节点分配内存失败!\n");
		return FAILURE;
	}

	(*root)->value = value;
	CreateBiTree(&((*root)->left));
	CreateBiTree(&((*root)->right));
}

先中后序遍历二叉树

以下先中后序三种遍历都有两种形式：递归版和非递归版（借助栈）

• 总是先遍历左子树,访问每个节点的左子树一直到最深,然后返回父节点访问兄弟右子树,以此类推。
• 打印当前节点关键字的时机不同:
  1.先根周游:第一次访问到该节点就直接打印
  2.中根周游:左子树全部遍历完才打印当前节点
  3.后根周游:左子树与右子树都遍历完才打印当前节点

先根周游（先序遍历）

• 递归版

void PreOrderBiTree(BiTree root) {
	if (root == NULL)
		return;
	printf("%d ", root->value);
	PreOrderBiTree(root->left);
	PreOrderBiTree(root->right);
}

• 非递归版
  1.将根结点入栈；
  2.每次从栈顶弹出一个结点，访问该结点；
  3.把当前结点的右儿子入栈；
  4.把当前结点的左儿子入栈。
  分析：出栈顺序就与递归先根周游一样：根节点->左节点->右节点

void PreOrderBiTreeByStack(BiTree root) {
	if (root == NULL)
		return;
	stack<BiTree> stk;
	stk.push(root);
	while (!stk.empty()) {
		BiTree curNode = stk.top();
		stk.pop();
		cout << curNode->value << endl;
		if (curNode->right != NULL)
			stk.push(curNode->right);
		if (curNode->left != NULL)
			stk.push(curNode->left);
	}
}

中根周游（中序遍历）

• 递归版

void InOrderBiTree(BiTree root) {
	if (root == NULL)
		return;
	InOrderBiTree(root->left);
	printf("%d ", root->value);
	InOrderBiTree(root->right);
}

• 非递归版
  1.初始化一个二叉树结点curNode指向根结点；
  1.若curNode非空，那么就把curNode入栈，并把curNode变为其左儿子；（直到最左边的结点）
  1.若curNode为空，弹出栈顶的结点，并访问该结点，将curNode指向其右儿子（访问最左边的结点，并遍历其右子树）

void InOrderBiTreeByStack(BiTree root) {
	if (root == NULL)
		return;
	stack<BiTree> stk;
	BiTree curNode = root;
	while (curNode != NULL || !stk.empty())
		if (curNode != NULL) {
			stk.push(curNode);
			curNode = curNode->left;
		}
		else {
			curNode = stk.top();
			stk.pop();
			cout << curNode->value << endl;
			curNode = curNode->right;
		}
}

后根周游（后序遍历）

• 递归版

void PostOrderBiTree(BiTree root) {
	if (root == NULL)
		return;
	PostOrderBiTree(root->left);
	PostOrderBiTree(root->right);
	printf("%d ", root->value);
}

• 非递归版
  1.设置两个栈stk1, stk2；
  2.将根结点压入第一个栈stk1；
  3.弹出stk1栈顶的结点，并把该结点压入第二个栈stk2；
  4.将当前结点的左儿子和右儿子先后分别入栈stk1；
  5.当所有元素都压入stk2后，依次弹出stk2的栈顶结点，并访问之。
  分析：第一个栈的入栈顺序是：根结点，左儿子和右儿子；于是，压入第二个栈的顺序是：根结点，右儿子和左儿子。因此，弹出的顺序就是：左儿子，右儿子和根结点。

void PostOrderBiTreeByStack(BiTree root) {
	if (root == NULL)
		return;
	stack<BiTree> stk1, stk2;
	stk1.push(root);
	while (!stk1.empty()) {
		BiTree cNode = stk1.top();
		stk1.pop();
		stk2.push(cNode);
		if (cNode->left != NULL)
			stk1.push(cNode->left);
		if (cNode->right != NULL)
			stk1.push(cNode->right);
	}
	while (!stk2.empty()) {
		cout << stk2.top()->value << endl;
		stk2.pop();
	}
}

层次遍历

• 层次遍历是指：按从根节点所在的层到最深的叶节点所在层遍历，然后逐层从左往右遍历
• 层次遍历是通过队列(先进先出)实现的(类似于广度优先搜索BFS，以上借助栈的非递归版相当于深度优先搜索DFS)。访问根节点并入队列。当队列不为空时，队列头结点出队列，并访问出队列的节点。如果它的左儿子不为空，将左儿子入队列，若果它的右儿子不为空，将它的右儿子入队列。重复操作直到队列为空
• 这样会在每层中从左到右访问节点，实现从根节点往下的按层遍历。

//利用队列进行层次遍历
void levelOrderBiTree(BiTree root) {
	if (root == NULL)
		return;
	queue<BiTree> que;
	BiTree frontNode = NULL;
	que.push(root);

	while (!que.empty()) {
		frontNode = que.front();//队头的指针赋给辅助操作指针
		cout << frontNode->value << endl;
		que.pop();//队头出队
		if (frontNode->left != NULL)//左儿子不为空左儿子入队
			que.push(frontNode->left);
		if (frontNode->right != NULL)//右儿子不为空右儿子入队
			que.push(frontNode->right);
	}
}

递归遍历的时间复杂度

• 二叉树遍历的递归实现中，每个结点只需遍历一次，故时间复杂度为O(n)；最差情况下递归调用的深度为O(n)，所以空间复杂度为O(n)。
• 二叉树遍历的非递归实现中，每个结点只需遍历一次，故时间复杂度为O(n)。空间复杂度为二叉树的高度，故空间复杂度为O(n)。

计算二叉树深度

//返回一棵二叉树的最大深度
int MaxDepthOfBiTree(BiTree root) {
	if (root == NULL)
		return 0;
	int max_left = MaxDepthOfBiTree(root->left);
	int max_right = MaxDepthOfBiTree(root->right);
	if (max_left > max_right)
		return 1 + max_left;
	else
		return 1 + max_right;
}

计算树叶的数量

//返回一颗二叉树树叶的数量(同时树叶也可衡量二叉树的深度 其中 sum of leaves = 2^depth)
int SumOfLeaveNode(BiTree root) {
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)//找到一个树叶
		return 1;
	else
		return SumOfLeaveNode(root->left) + SumOfLeaveNode(root->right);
}

通过先根周游（或后根周游）和中根周游结果建立二叉树

• 思路: 先根周游的顺序是根左右（后根是左右根），中根周游的顺序是左根右。根据这个特性，先序遍历的结果中第一个肯定是根节点（对应的，后根结果中最后一个肯定是根节点），而在中序遍历结果中找到这个根节点，对中序而言，这个根节点的左侧是左子树，右侧是右子树。得到子树后，便重复上述过程 [对上次操作分离出的待建立子树，在先序遍历（或后根遍历）结果中找到这一部分子序列，该序列首节点又是这个子树的根节点] 。如此便可递归地创建二叉树。

//通过一棵树的先根周游和中根周游结果，建立原树 
BiTree CreateBiTreeByPreAndIn(int *inOrder, int *preOrder, int length) {
	int i, index = 0;
	if (length == 0)
		return NULL;
	BiTree root = (BiTree)malloc(sizeof(BiNode));
	root->value = preOrder[0];
	for (i = 0;i < length;i++)
		if (inOrder[i] == preOrder[0])
			index = i;
	root->left = CreateBiTreeByPreAndIn(inOrder, preOrder + 1, index);
	root->right = CreateBiTreeByPreAndIn(inOrder + (index + 1), preOrder + (index + 1), length - (index + 1));
	return root;
}
//通过后根与中根周游结果建立原树，与上个函数类似
BiTree CreateBiTreeByPostAndIn(int *inOrder, int *postOrder, int length) {
	int i, index = 0;
	if (length == 0)
		return NULL;
	BiTree root = (BiTree)malloc(sizeof(BiNode));
	root->value = postOrder[length - 1];
	for (i = 0;i < length;i++)
		if (inOrder[i] == postOrder[length - 1])
			index = i;
	root->left = CreateBiTreeByPostAndIn(inOrder, postOrder, index);
	root->right = CreateBiTreeByPostAndIn(inOrder + (index + 1), postOrder + index, length - (index + 1));
	return root;
}

Morris遍历算法

• Morris算法在遍历的时候避免使用了栈结构，而是让下层到上层有指针，具体是通过底层节点指向NULL的空闲指针返回上层的某个节点，从而完成下层到上层的移动。由前述思考可知，二叉树有很多空闲的指针，比如某个节点没有右儿子，我们称这种情况为空闲状态，Morris算法的遍历正是利用了这些空闲的指针使得遍历算法的时间复杂度得到巨大优化。
• 只需要常数的空间即可在O(n)时间内完成二叉树的遍历。O(1)空间进行遍历困难之处在于在遍历子节点的时候如何重新返回其父节点，而在Morris遍历算法中，通过修改叶子结点的左右空指针来指向其前驱或者后继结点来解决此困难。

由中根周游Morris版引入其算法思想：

1.如果当前结点pNode的左儿子为空，那么输出该结点，并把该结点的右儿子作为当前结点；
2.如果当前结点pNode的左儿子非空，那么就找出该结点在中序遍历中的前驱结点pPre
3.当第一次访问该前驱结点pPre时，其右儿子必定为空，那么就将其右儿子设置为当前结点，以便根据这个指针返回到当前结点pNode中，并将当前结点pNode设置为其左儿子；
4.当该前驱结点pPre的右儿子为当前结点，那么就输出当前结点，并把前驱结点的右儿子设置为空（恢复树的结构），将当前结点更新为当前结点的右儿子
5.重复以上两步，直到当前结点为空。

//由中根周游引入
void InOrderBiTreeByMorris(BiTree root) {
	if (root == NULL)
		return;
	BiTree pNode = root;
	while (pNode != NULL) {
		if (pNode->left == NULL) {
			cout << pNode->value << endl;
			pNode = pNode->right;
		}
		else {
			BiTree pPre = pNode->left;
			while (pPre->right != NULL && pPre->right != pNode)
				pPre = pPre->right;
			if (pPre->right == NULL) {
				pPre->right = pNode;
				pNode = pNode->left;
			}
			else {
				pPre->right = NULL;
				cout << pNode->value << endl;
				pNode = pNode->right;
			}
		}
	}
}

• 分析：
  因为只使用了两个指针作辅助，所以空间复杂度为O(1)。对于时间复杂度，每次遍历都需要找到其前驱的结点，而寻找前驱结点与树的高度相关，那么直觉上总的时间复杂度为O(nlogn)。其实，并不是每个结点都需要寻找其前驱结点，只有左子树非空的结点才需要寻找其前驱，所有结点寻找前驱走过的路的总和至多为一棵树的结点个数。因此，整个过程每条边最多走两次，一次是定位到该结点，另一次是寻找某个结点的前驱，所以时间复杂度为O(n)。
  

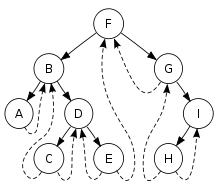
  如上图这棵二叉树。首先，访问的是根结点F，其左儿子非空，所以需要先找到它的前驱结点（寻找路径为B->D->E），将E的右指针指向F，然后当前结点为B。依然需要找到B的前驱结点A，将A的右指针指向B，并将当前结点设置为A。下一步，输出A，并把当前结点设置为A的右儿子B。之后，会访问到B的前驱结点A指向B，那么令A的右指针为空，继续遍历B的右儿子，以此类推。

Morris先根周游版

与中序遍历类似，只是输出关键字的顺序不同

void PreOrderBiTreeByMorris(BiTree root) {
	if (root == NULL)
		return;
	BiTree pNode = root;
	while (pNode) {
		if (pNode->left == NULL) {
			cout << pNode->value << endl;
			pNode = pNode->right;
		}
		else {
			BiTree pPre = pNode->left;
			while (pPre->right != NULL && pPre->right != pNode)
				pPre = pPre->right;

			if (pPre->right == NULL) {
				pPre->right = pNode;
				cout << pNode->value << endl;
				pNode = pNode->left;
			}
			else {
				pPre->right = NULL;
				pNode = pNode->right;
			}
		}
	}
}

Morris后根周游版

• 先建立一个临时结点dummy，并令其左儿子为根结点root，将当前结点设置为dummy；
• 如果当前结点的左儿子为空，则将其右儿子作为当前结点；
• 如果当前结点的左儿子不为空，则找到其在中序遍历中的前驱结点：
  1.如果前驱结点的右儿子为空，将它的右儿子设置为当前结点，将当前结点更新为当前结点的左孩子；
  2.如果前驱结点的右儿子为当前结点，倒序输出从当前结点的左儿子到该前驱结点这条路径上所有的结点。将前驱结点的右儿子设置为空，将当前结点更新为当前结点的右儿子。
• 重复以上过程，直到当前结点为空。

void reverse(BiTree p1, BiTree p2) {
	if (p1 == p2)
		return;
	BiTree x = p1;
	BiTree y = p1->right;
	while (true) {
		BiTree temp = y->right;
		y->right = x;
		x = y;
		y = temp;
		if (x == p2)
			return;
	}
}

void printReverse(BiTree p1, BiTree p2) {
	reverse(p1, p2);

	BiTree curNode = p2;
	while (true) {
		cout << curNode->value << endl;
		if (curNode == p1)
			break;
		curNode = curNode->right;
	}

	reverse(p2, p1);
}

void PostOrderBiTreeByMorris(BiTree root) {
	if (root == NULL)
		return;

	BiTree dummy = new BiNode(-1);
	dummy->left = root;
	BiTree pNode = dummy;
	while (pNode != NULL) {
		if (pNode->left == NULL)
			pNode = pNode->right;
		else {
			BiTree pPre = pNode->left;
			while (pPre->right != NULL && pPre->right != pNode)
				pPre = pPre->right;

			if (pPre->right == NULL) {
				pPre->right = pNode;
				pNode = pNode->left;
			}
			else {
				printReverse(pNode->left, pPre);
				pPre->right = NULL;
				pNode = pNode->right;
			}
		}
	}
}

---

扩展概念

二叉查找树ADT

基础概念

• 假设任意节点的关键字都是互异的（简化）
• 对于普通二叉树中的每个节点X，它的左子树中所有关键字值都小于X的关键字值，而它的右子树中所有关键字值都大于X的关键字值
• 由于每个节点的关键字值都是按一定顺序排列的，也就为普通二叉树新增了增删改查操作

建立空树

• 置空一颗树，只保留根节点

BiTree makeEmptyTree(BiTree root) {
	if (root != NULL) {
		makeEmptyTree(root->left);
		makeEmptyTree(root->right);
		free(root);
	}
	return NULL;
}

增删改查

插入insert

• 思路：将要插入节点的键值与根节点键值比较，如果小于根节点键值，则插入根节点的左子树，如果大于根节点的键值，则插入根节点的右子树，插入子树相当于插入一个更小的树，因此可以用递归方法实现，直到找到没有子树的节点，将新节点插到其下面。注意，新节点插入后，最终只会成为叶节点。
• 递归版

BiTree insertNode(BiTree curNode, int value) {
	if (curNode == NULL) {
		//curNode为空则新建一个节点
		curNode = (BiTree)malloc(sizeof(BiNode));
		curNode->value = value;
		curNode->left = curNode->right = NULL;
	}
	else if (value < curNode->value)
		curNode->left = insertNode(curNode->left, value);
	else if (value > curNode->value)
		curNode->right = insertNode(curNode->right, value);

	return curNode;
}

• 非递归版

//非递归插入
void insertNode_Ex(BiTree root, int value) {
	BiTree *pNode;//BiNode的二级指针，解引用
	//root作为参数传值时是一颗查找树的根节点指针，在接下来的操作里可视作curNode作辅助指针
	while (root != NULL) {
		if (value < root->value) {
			pNode = &(root->left);
			root = root->left;
		}
		else if (value > root->value) {
			pNode = &(root->right);
			root = root->right;
		}
		else
			return;//等于当前节点的关键字值，说明已存在
	}
	//前述遍历完后,pNode中存放的是待插入节点的父节点的子节点指针（左儿子或右儿子）的地址
	*pNode = (BiTree)malloc(sizeof(BiNode));
	(*pNode)->value = value;
	(*pNode)->left = (*pNode)->right = NULL;
}

删除delete

• 思路：删除节点后，要调整各节点的位置(即改变指针引用)才能使剩下的节点组成的树仍为二叉查找树
  1.如果节点X是一片树叶（节点X没有儿子），直接删除该节点（父节点指向该节点的指针置空，接着释放内存）
  2.如果节点X有一个儿子，为父节点parentX调整指针绕过该节点指向节点X的子节点childX，接着操作同上。
  3.如果节点X有两个儿子。删除策略：用节点X的右子树中的最小元代替该节点的关键字值并递归地删除那个原最小元所在的节点。分析：右子树的最小元所在节点不可能有左儿子，此时调用前例情况1或2删除。

BiTree deleteNode(BiTree curNode, int value) {
	BiTree tempNode;
	if (curNode == NULL)
		return NULL;
	if (value < curNode->value)
		curNode->left = deleteNode(curNode->left, value);
	else if (value > curNode->value)
		curNode->right = deleteNode(curNode->right, value);
	else if (curNode->left != NULL && curNode->right != NULL) {
		//目标节点左儿子与右儿子都存在
		//Replace with the smallest element in right subtree
		tempNode = findMin(curNode->right);//findMin为后文查询操作里用以寻找最小元的函数
		curNode->value = tempNode->value;
		curNode->right = deleteNode(curNode->right, curNode->value);
	}
	else {
		//一个儿子或没有儿子
		tempNode = curNode;
		curNode = curNode->left != NULL ? curNode->left : curNode->right;
		free(tempNode);//释放内存
	}
	return curNode;
}

查找find

• 给定要寻找的节点的关键字和树的根节点指针，只需根据二叉查找树的性质递归找到该节点

//find操作
BiTree find(BiTree curNode, int value) {
	if (curNode == NULL)
		return NULL;
	if (value < curNode->value)
		return find(curNode->left, value);
	else if (value > curNode->value)
		return find(curNode->right, value);
	else
		return curNode;
}

//给定根节点找出其树的最小元(由ADT性质，总是在左子树里寻找)
BiTree findMin(BiTree root) {
	if (root == NULL)
		return NULL;
	else
		if (root->left == NULL)
			return root;
		else
			return findMin(root->left);
}

//给定根节点找出其树的最大元(由ADT性质，总是在右子树里寻找)
BiTree findMax(BiTree root) {
	if (root == NULL)
		return NULL;
	else
		if (root->right == NULL)
			return root;
		else
			return findMax(root->right);
}

修改update

int updateNode(BiTree root, int src, int dst) {
	if (root == NULL)
		//树中不存在源操作数元的节点
		return FAILURE;
	if (src < root->value)
		return updateNode(root->left, src, dst);
	else if (src > root->value)
		return updateNode(root->right, src, dst);
	else if(src = root->value){
		root->value = dst;
		return SUCCESS;
	}
}

前述操作的时间复杂度

• 平均情形分析：
  1.直观上，前述的增删改查操作都花费O(log N)时间，因为用常数时间在树中降低了一层，这导致对树的操作大概减少一半。所有的操作都是O(d)，其中d是包含所访问的关键字的节点的深度。

  内部路径长： 一棵树的所有节点的深度的和称为内部路径长(internal path length)。

  2.由前述内部路径长定义，如下计算二叉查找树平均内部路径长，此处 平均 是相对于向二叉查找树中所有可能的插入序列进行的。

• 具体分析：
  令 D(N) 是具有N个节点的某棵树T的内部路径长，D(1) = 0。一颗 N 节点树是由一颗 i 节点左子树和一颗 (N - i - 1) 节点右子树以及深度为0的一个根节点组成，其中0 <= i <= N，D(i) 为根的左子树的内部路径长。但是在原树中，所有这些节点都要加深一度。同样的结论对于右子树依然成立。如此可得递归关系:
  $$D(N)=D(i)+D(N-i-1)+N-1$$
  如果所有子树的大小等可能地出现(对于ADT是成立的，子树的大小只依赖于第一个插入到树中的元素的相对的秩，而对于普通二叉树则不成立)，那么 D(i) 和 D(N - i - 1)的平均值都是$\frac{1}{N}{\sum }_{j=0}^{N-1}D(j)$。于是则有：
  $$D(N)=\frac{2}{N}[\sum _{j=0}^{N-1}D(j)]+N-1$$

简化上式以方便分析

$$T(N)=\frac{2}{N}[\sum _{j=0}^{N-1}T(j)]+cN$$

用N乘以上式

$$NT(N)=2[\sum _{j=0}^{N-1}T(j)]+c{N}^2$$

用 N=N-1替换上式中的N

$$(N-1)T(N-1)=2[\sum _{j=0}^{N-2}T(j)]+c(N-1{)}^2$$

上述两式作差除去求和符号

$$NT(N)-(N-1)T(N-1)=2T(N-1)+2cN-c$$

移项、合并并除去右边无关紧要的常数c

$$NT(N)=(N+1)T(N-1)+2cN$$
$$\frac{T(N)}{N+1}=\frac{T(N-1)}{N}+\frac{2c}{N+1}$$

进行叠缩

$$\frac{T(N-1)}{N}=\frac{T(N-2)}{N-1}+\frac{2c}{N}$$
$$\frac{T(N-2)}{N-1}=\frac{T(N-3)}{N-2}+\frac{2c}{N-1}$$
$$...$$
$$\frac{T(2)}{3}=\frac{T(1)}{2}+\frac{2c}{3}$$

前述式子逐项相加

$$\frac{T(N)}{N+1}=\frac{T(1)}{2}+2c\sum _{i=3}^{N+1}\frac{1}{i}\approx ln(N+1)+\gamma -\frac{3}{2}$$
$$欧拉常数(Eule{r}^{\prime }sconstant)\gamma \approx 0.577$$

于是立刻有

$$\frac{T(N)}{N+1}=O(logN)$$
$$T(N)=O(NlogN)$$

• 结论：得到的二叉查找树平均内部路径长为$D(N)=O(NlogN)$。因此任意节点的期望深度为$d(N)=O(logN)$。

---

平衡二叉查找树

带有平衡条件的二叉查找树

• 由前述计算二叉查找树平均内部路径长并据此求期望深度的过程中，明确“平均”意味着什么一般是极其困难的，如果一棵树极不平衡(例如整棵树左沉或右沉: 一颗子树的深度远远大于另一颗子树时)，以上递归操作付出的代价是极为巨大的（例如退化成近似单向链表的最坏情形时，对这颗二叉树的一连串Insert操作将会花费二次时间）。
• 要避免以上情况的出现可以为二叉查找树附加一个称为“平衡”的结构条件：任何节点的深度不宜过深。并在操作过程中根据平衡条件实时调整树的结构，将会大幅提高效率。

AVL树(Adelson-Velskii & Landis)²

基本概念

• AVL树是最老的一种平衡查找树
• AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树(空树高度定义为-1)，因此也被称为高度平衡树。

性质

• 暂且留白，以后填坑。延伸阅读: AVL tree -Wikipedia

伸展树(Splay tree)³

基本概念

• Splay tree(伸展树)是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去
• 这种树放弃了前述的平衡条件， 允许树有任意的深度，但是在每次操作后要使用一个调整规则进行调整。
• 对于任意单个运算，不再保证$O(logN)$的时间界，但是可以证明任意连续M次操作在最坏的情形下花费时间$O(MlogN)$，足以防止出现前述查找树的最坏条件：退化成单向链表的二叉树。

性质

• 暂且留白， 以后填坑。延伸阅读: Splay tree -Wikipedia

---

1. 《数据结构与算法分析：C语言描述》 / （美）Mark Allen Weiss著 ↩︎

2. Georgy Adelson-Velsky, G.; Evgenii Landis (1962). “An algorithm for the organization of information”. Proceedings of the USSR Academy of Sciences (in Russian). 146: 263–266. English translation by Myron J. Ricci in Soviet Mathematics - Doklady, 3:1259–1263, 1962. ↩︎

3. Albers, Susanne; Karpinski, Marek (28 February 2002). “Randomized Splay Trees: Theoretical and Experimental Results” (PDF). Information Processing Letters. 81 (4): 213–221. doi:10.1016/s0020-0190(01)00230-7. ↩︎