深度学习中的激活函数总结

激活函数饱和问题

一个激活函数$h(n)$，当n趋近于正无穷，激活函数的导数趋近于0，称之为右饱和；当n趋近于负无穷，激活函数的导数趋近于0，称之为左饱和。
当一个函数既满足左饱和又满足右饱和的时候我们称之为饱和。
不满足上述两个条件的，称为不饱和激活函数。
常见的激活函数，依照饱和或不饱和划分如下：
饱和激活函数：

• sigmoid
• tanh

不饱和激活函数：

• ReLU
• Leaky ReLU
• PReLU
• Swish
• Mish

常用激活函数

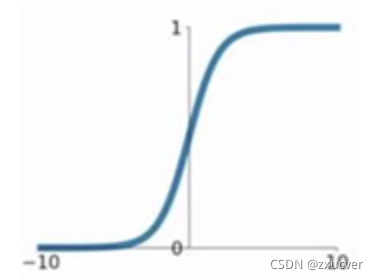
sigmoid

$$g(z)=\frac{1}{1+e^{-z}}$$

$$g^{\prime }(z)=(\frac{1}{1+e^{-z}}{)}^{\prime }=\frac{e^{-z}}{(1+e^{-z}{)}^2}=g(z)(1-g(z))$$
sigmoid函数的问题在于当Z值非常大或者非常小的时候，会导致其导数趋近于零，也就是权重的梯度趋近于零，即梯度消失。

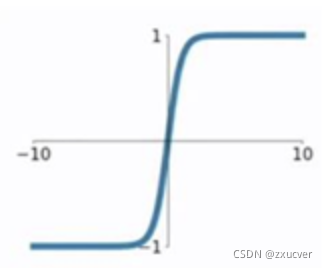
tanh

tanh相较于sigmoid函数要常见一些，该函数是将取值为 (−∞,+∞) 的数映射到 (−1,1) 之间。

$$g(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$
$$g^{\prime }(z)=(\frac{e^z-e^{-z}}{e^z+e^{-z}}{)}^{\prime }=\frac{4}{(e^z+e^{-z}{)}^2}=1-g(z{)}^2$$
tanh函数的缺点同sigmoid函数的第一个缺点一样，当 z 很大或很小时，g′(z) 接近于 0 ，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。

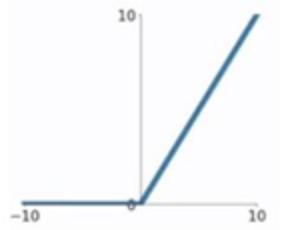
ReLU

$$g(z)=\{\begin{array}{r}z,if:z>0\\ z,if:z<0\end{array}$$
$$g^{\prime }(z)=\{\begin{array}{r}1,if:z>0\\ 0,if:z<0\end{array}$$
ReLU函数的优点：

• 在输入为正数的时候（对于大多数输入 z 空间来说），不存在梯度消失问题。
• 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）

ReLU函数的缺点：

• 当输入为负时，梯度为0，会产生梯度消失问题。

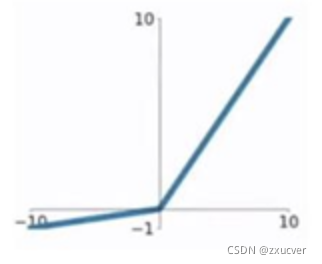
Leaky ReLU

它是一种对ReLU函数改进的函数，又称为PReLU函数。

$$g(z)=\{\begin{array}{r}z,if:z>0\\ az,if:z<0\end{array}$$
$$g^{\prime }(z)=\{\begin{array}{r}1,if:z>0\\ a,if:z<0\end{array}$$
Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题。

Swish

Swish 在深层模型上的效果优于 ReLU。可以看做是介于线性函数与ReLU函数之间的平滑函数.

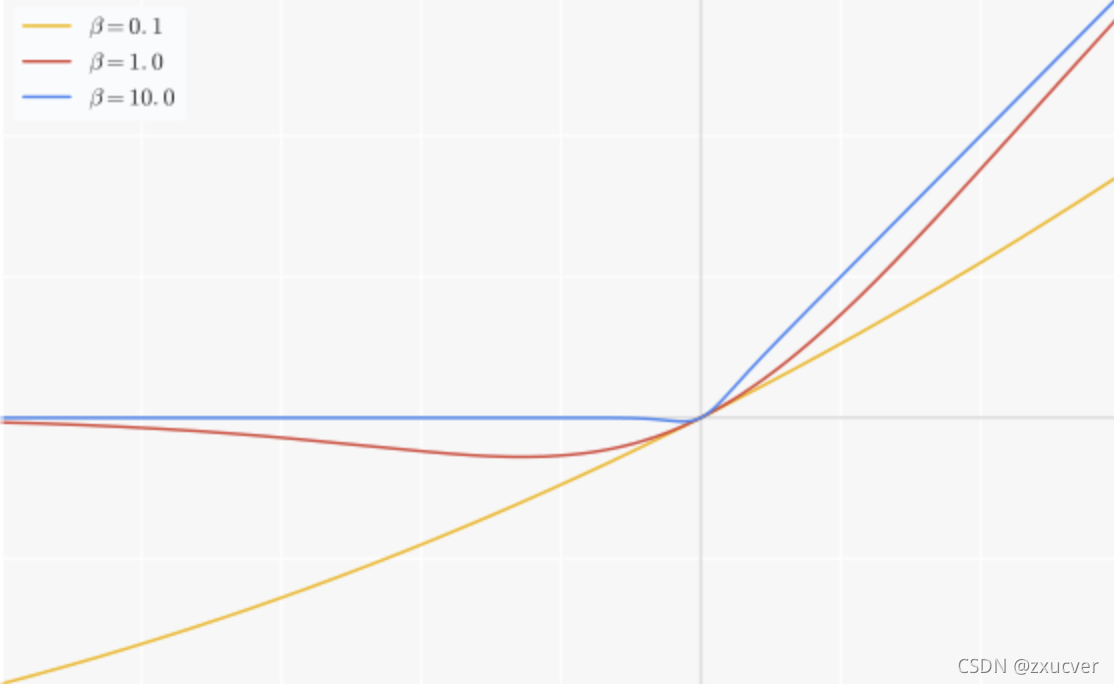
Swish与ReLU，PReLU最大的区别在于，有下界，平滑，非单调。

Mish

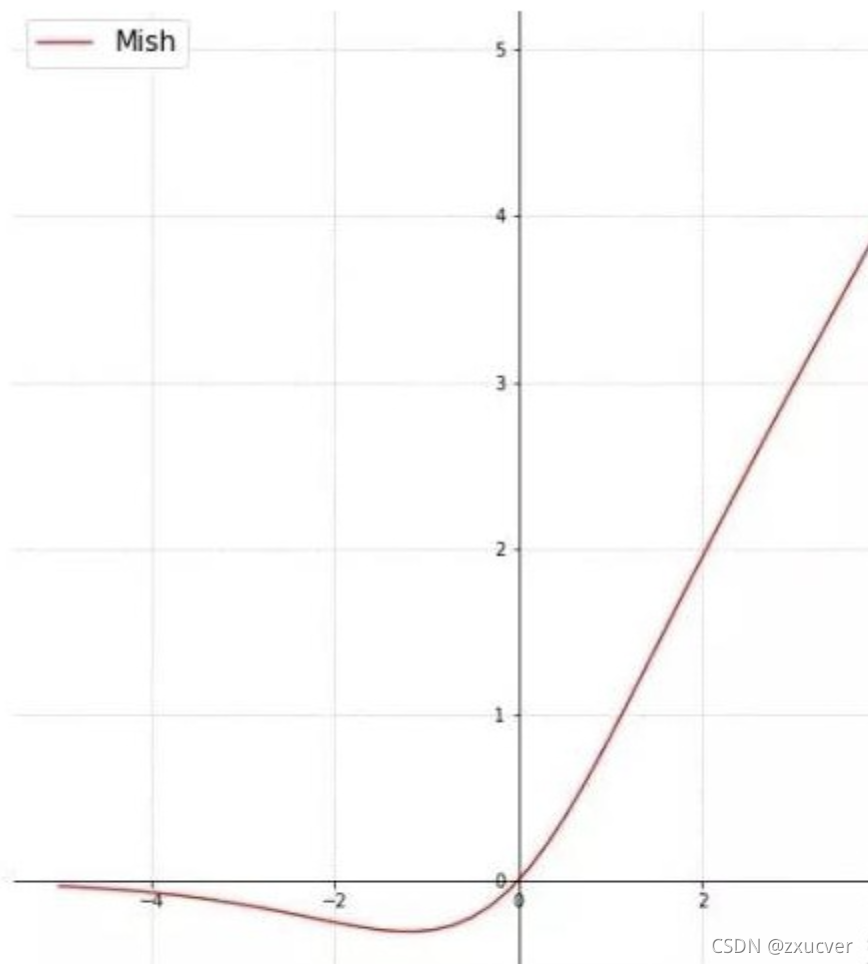
Mish与Swish非常相似，同样具备有下界，平滑，非单调的特点。