深度学习基础之激活函数

---

---

1.激活函数的作用

激活函数是对输入做的一种非线性的转换，其目的是把当前特征空间通过一定的映射转换到另一个空间，让数据能够更好的被分类。

在下图中：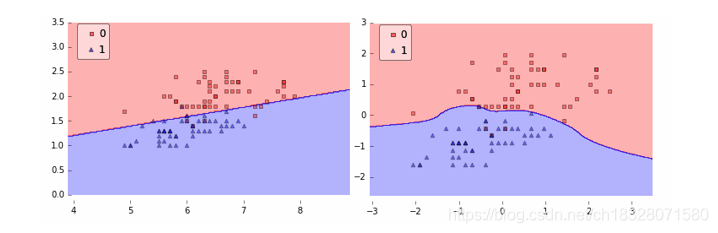
左图假设数据是线性可分的，只需要一条直线就已经能够对样本进行很好地分类。然而，在实际中数据如右图，简单的一条直线不能够对样本进行很好地分类。因此，需要引入一些非线性的因素，来更好地解决复杂的问题。而激活函数恰好能引入非线性因素，它使得神经网络能够更好地解决较为复杂的问题。

所以，引入的激活函数往往是非线性的，使用非线性激活函数 $f(x)$ ，以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性激活函数，能够从输入输出之间生成非线性映射。

2.激活函数的相关概念

在ICML2016的一篇论文Noisy Activation Functions中，作者将激活函数定义为一个几乎处处可微的 $h:R\to R$ 。

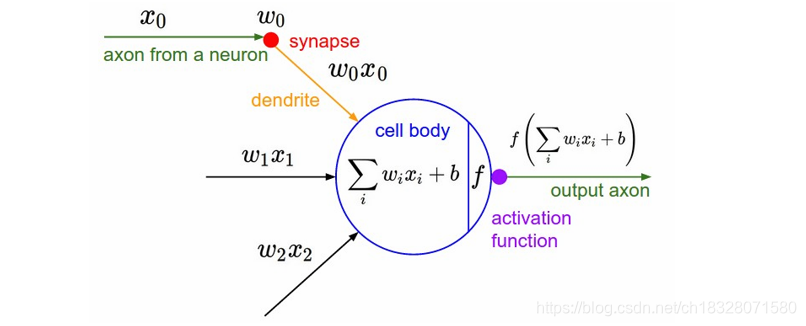
还有以下的一些概念：

a.饱和

当一个激活函数$h(x)$满足
$$\underset{n\to +\infty }{\lim }{h}^{\prime }(x)=0$$
时,称之为右饱和。

当一个激活函数$h(x)$满足
$$\underset{n\to -\infty }{\lim }{h}^{\prime }(x)=0$$
时,称之为左饱和。

当一个激活函数，既满足左饱和又满足又饱和时，我们称之为饱和。

b.硬饱和与软饱和

对任意的$x$，如果存在常数$c$，当$x>c$时恒有 h ’ ( x ) = 0 h’(x)