31 生成对抗网络 GAN

1 什么是 Generative Adversarial Network ?

首先,我们需要充分的了解什么是生成对抗网络( tive adversarial network,GAN)?顾名思义, 首先它是一种生成模型,它的核心是对样本数据建模。下面我们将举个例子来详细的说明一下什么是GAN。
首先,我是一个收藏家,我有很多的宝贝,但是,我最终的目标不仅仅是一个收藏家。我想高仿东西,成为工艺品大师(做仿品)。我要不惜一切代价的成为这方面的大师。但是,我做出来的东西不能只是我白己分辨不出来就够了,那就只能放在家里看,它需要接受大师们的检验,各位专家都看不出来这是仿品,就比较成功了。
我把我做出的东西,放到一个叫“一锤定音”节口现场,这个平台将鉴别出为假的东西就砸了,鉴别出为真的东西就拿去估值,就美了。节囗流程如下所示

我们的目标是成为高水平的可以做“以假乱真”的高质量仿品的大师,有如下两个要求：

1. 鉴赏专家的水平足够高
2. 作假的水平足够高。

国宝是古人做的,静态的,不可能发生变化的。而工艺品和作假的水平是变化的。三者中,国宝是静态的,其他的都是可变化的。
有可能有的同学会迷惑,这和生成模型之间有什么关系呢?如果一个仿品可以和国宝做的一模样,不就相当于学到了真实数据的分布,可以完全模拟出真实数据。下一步则是,想办法将模型用数学语言描述。

2数学语言描述

2.1 模型表示

工艺大帅和鉴赏专家的水平会不断的提高,最终我们会培养一个高水平的工艺大师和一个高水平的鉴赏家。而最终的口的是培养一个高水平的工艺大师,而不是一个高水平的鉴赏家。鉴赏家只是衍生品,最终将达到两个口的,1.足够的以假乱真;2.真正的专家看不出来
所以,我们需要加一些 feedback,令工艺大师收到专家给出的反馈。并且鉴赏大师也要从工艺大师那里知道真实的情况来提升自己的水平。如下图所示:

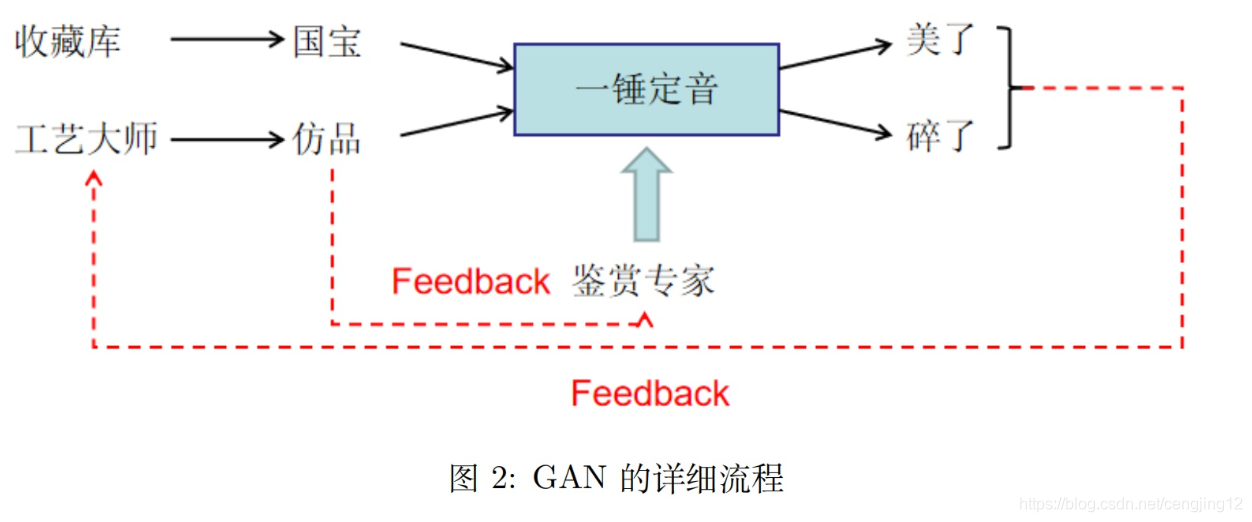
我们可以将古人，视为 Pdata ,{xi}i=1N,P_{\text {data }},\left\{x_{i}\right\}_{i=1}^{N},Pdata ​,{xi​}i=1N​, 实际就是经验分布，通常我们将经验分布视为数据分布。 工艺品，是从一个模型分布 $P_g$ 采样出来的， $P_g\left(x;{\theta }_g\right)$ 。我们本身不对 $P_g$ 建模，而是用一个神经网络来逼近 $P_{g\circ }$ 假设 $z$ 来自一个简单分布，并增加噪声， $z\sim P_z(z)$ 。其中 $,x=G\left(z;{\theta }_g\right)$

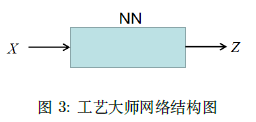
鉴赏专家输出的是一个概率分布，同样也是一个神经网络，D $\left(x,{\theta }_d\right),$ 其代表的基输入一个物品判断其为国宝的概率。D $\to 1$ 是国宝， $D\to 0$ 是工艺品。模型如下所示：

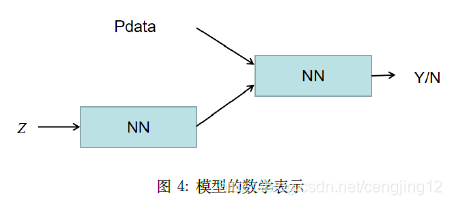
我们的目标有两个：

1. 高专家：高水平的专家可以正确的分辨国宝和尖品。
   $$\{\begin{array}{l}\text{ if }x\text{ is from }{P}_{\text{data }}\text{ then }D(x)\uparrow \\ \text{ if }x\text{ is from }{P}_g\text{ then }1-D(x)\downarrow \end{array}$$
   其中，我们将用对数似然函数的形式来进行表达。而 $1-D(x)$ 中的 $x$ 是来自 $G(z)$ 的，那么，高专家部分的目标函数为：
   $$\underset{D}{\max }\underset{\frac{1}{N}{\sum }_{i=1}^N\log D\left(x_i\right)}{{\mathbb{E}}_{x\sim P_{\text{data}}}[\log D(x)]}+{\mathbb{E}}_{x\sim P_z}[\log (1-D(G(z)))]$$
2. 高大师: 高水平的大师的目的就是要造成高水平的鉴赏专家分辨不出来的工艺品，可以表示为：
   $$\text{ if }x\text{ is from }{P}_g\text{ then }\log (1-D(G(z)))\uparrow$$
   此目标表达为数学语言即为：
   $$\underset{G}{\min }{\mathbb{E}}_{z\sim P_g}[\log (1-D(z))]$$
   根据图 2 中的 feedback 流向，我们可以了解到，先优化鉴赏专家，再优化工艺大师。总优化目标是：
   $$\underset{G}{\min }\underset{D}{\max }{\mathbb{E}}_{x\sim P_{\text{data }}}[\log D(x)]+{\mathbb{E}}_{x\sim P_z}[\log (1-D(G(z)))]$$

2.2 小结

GAN 模型本身思想很简单，难点主要在于学习 ${\theta }_g,{\theta }_d$ 。GAN 中没有直接面向 $P_g$ 建模，而是从一 个可微的 NN 中采样来逼近 $D_g\left(x;{\theta }_g\right)$ 。不是直接面对分布，而是绕过复杂的求解过程来近似。我们之 前分析过，如果用 NN 来近似概率分布，这叫 Implicit Density Model。下一步则是考虑如何求解全局最优解。

3 全局最优解

GAN 模型表示汇总如下所示：

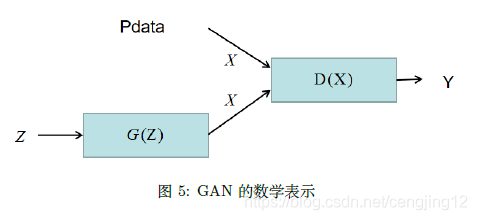
Pdata:{xi}i=1NPg(x;θg): generator ,G(z;θg)y∣x: discriminater ,P(y=1∣x)=D(x),P(y=0∣x)=1−D(x)      (5) \begin{array}{l} P_{d a t a}:\left\{x_{i}\right\}_{i=1}^{N} \\ P_{g}\left(x ; \theta_{g}\right): \text { generator }, G\left(z ; \theta_{g}\right) \\ y | x: \text { discriminater }, P(y=1 | x)=D(x), P(y=0 | x)=1-D(x) \end{array} \ \ \ \ \ \ (5) Pdata​:{xi​}i=1N​Pg​(x;θg​): generator ,G(z;θg​)y∣x: discriminater ,P(y=1∣x)=D(x),P(y=0∣x)=1−D(x)​      (5)
$G\left(z;{\theta }_g\right)$ 和 $D\left(x;{\theta }_d\right)$ 是两个多层感知机。GAN 就是这样采用对抗学习，其最终目的就是 $P_g=$ $P_{\text{data }}$ 。目标函数中，记：
$$V(D,G)={\mathbb{E}}_{x\sim P_{\text{data}}[\log D(x)]}+{\mathbb{E}}_{x\sim P_z}[\log (1-D(G(z)))](6)$$
最终的目标是令 $P_g=P_{\text{data}},$ 而 $P_g$ 中的参数为 ${\theta }_g$ 。在之前的极大似然估计思想中,
$${\theta }_g=\arg \underset{{\theta }_g}{\max }\sum _{i=1}^N\log P_g\left(x_i\right)(7)$$
而对 $P_g\left(x_i\right)$ 比较复杂，通常采用 EM 算法和 VI 来进行近似，通过推导可以得出，最后的目标为：
$$\arg \underset{{\theta }_g}{\min }\mathrm{K}\mathrm{L}\left(P_{\text{data }}\Vert P_g\right)$$
对公式 (5) 的求解过程可以分成两步，而第一步为求解过依为 fixed G，求解 $ma{x}_{p}V(G,D)$
$$\begin{array}{rl}\underset{D}{\max }V(D,G)& =\int P_{\text{data }}\log Ddx+\int P_g\log (1-D)dx\\ & =\int \left(P_{\text{data }}\log Ddx+P_g\log (1-D)\right)dx\end{array}(8)$$
通过求偏导来计算最优解：
$$\begin{array}{rl}\frac{\partial (V(D,G))}{\partial D}& =\frac{\partial }{\partial D}\int \left[P_{\text{data }}\log Ddx+P_g\log (1-D)\right]dx\\ & =\int \frac{\partial }{\partial D}\left[P_{\text{data }}\log Ddx+P_g\log (1-D)\right]dx\\ & =0\end{array}$$
这一步的推导利用了微积分的基本定理，得到：
$$\int P_{\text{data }}\cdot \frac{1}{D}+P_g\frac{-1}{1-D}dx=0$$
恒成立，所以有：
$$D^{\ast }=\frac{P_{\text{data }}}{P_{\text{data }}+P_g}$$
第二步，将求解的是：
$$\begin{array}{rl}\underset{G}{\min }\underset{D}{\max }V(D,G)& =\underset{G}{\min }V\left(D^{\ast },G\right)\\ & =\underset{D}{\min }{\mathbb{E}}_{x\sim P_{\text{data }}}\left[\log \frac{P_{\text{data }}}{P_{\text{data }}+P_g}\right]+{\mathbb{E}}_{x\sim P_g}\left[\log \frac{P_g}{P_{\text{data }}+P_g}\right]\end{array}$$
观赛 ${\mathbb{E}}_{x\sim P_{\text{data }}}\left[\log \frac{P_{\text{ates }}}{P_{\text{dath }}+P_g}\right]$ 会发现这很像一个 $\mathrm{K}\mathrm{L}$ 散度，但是 $P_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}+P_g$ 不是一个板率分布。所以,
$$\begin{array}{rl}\underset{G}{\min }\underset{D}{\max }V(D,G)& =\underset{G}{\min }{\mathbb{E}}_{x\sim P_{\text{date }}}\left[\log \frac{P_{\text{data }}}{\frac{P_{\text{tata }}+P_g}{2}}\cdot \frac{1}{2}\right]+{\mathbb{E}}_{x\sim P_g}\left[\log \frac{P_g}{\frac{P_{\text{date }}+P_{\theta }}{2}}\cdot \frac{1}{2}\right]\\ & =\underset{G}{\min }\mathrm{K}\mathrm{L}\left[P_{\text{data }}\Vert \frac{P_{\text{data }}+P_g}{2}\right]+\mathrm{K}\mathrm{L}\left[P_g\Vert \frac{P_{\text{data }}+P_g}{2}\right]-\log 4\\ & \ge -\log 4\end{array}$$
当且仪当 $P_{\text{data }}=P_g=\frac{P_{\text{ata }}+P_9}{2}$ 寺，等号成立。此时 $,P_g^{\ast }=P_d,P_d^{\ast }=\frac{1}{2}$。 很显然，大家想一想就知道，生成器模型分布最好当然是和数据分布是一样的，而此时判别器模型真的和假的都分不出，输出都是 $\frac{1}{2}$。