【贪心算法】专题练习一

欢迎来到Cefler的博客😁
🕌博客主页：那个传说中的man的主页
🏠个人专栏：题目解析
🌎推荐文章：题目大解析（3）

---

前言
1.什么是贪心算法？——贪婪+鼠目寸光

贪心策略：解决问题的策略，局部最优->全局最优
(1)即把解决问题的过程分为若干步
(2)解决每一步的时候吗，都选择当前看起来“最优的”解法
（3）希望得到全局最优解

2.贪心算法的特点
(1) 贪心策略的提出是没有标准以及模板的
(2) 可能每一道题的贪心策略都是不同的
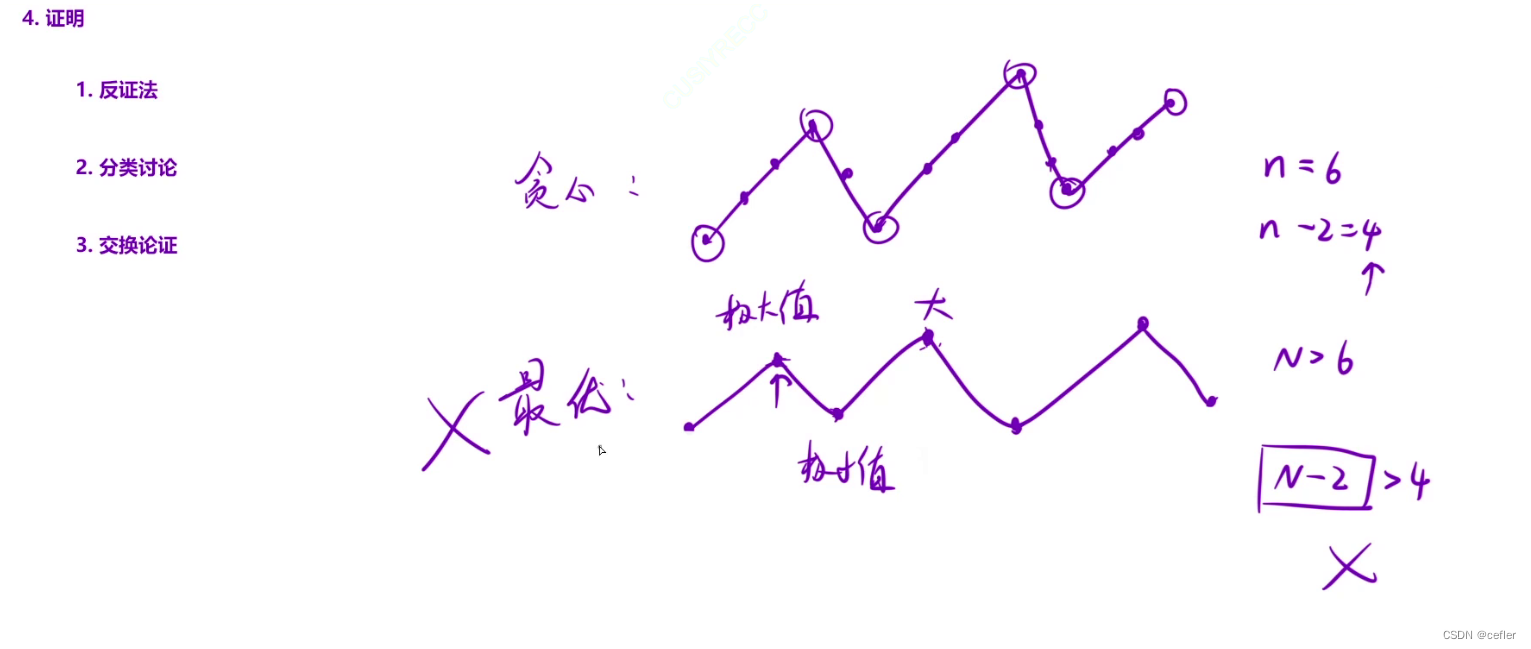
(3)贪心策略的正确性：可能会出错；正确的贪心策略，我们是需要“证明的”

3.证明贪心策略的方法:数学中见过的所有证明方法

4.学习贪心的方向
(1):遇到不会的贪心题，很正常，把心态放平
(2):把策略当成经验吸收
(3):能证明则证明贪心策略的正确性

---

👉🏻柠檬水找零

原题链接：柠檬水找零

mycode:

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int five = 0,ten = 0,twenty = 0;
        for(auto e:bills)
        {
            if(e==5)
            {
                five++;
            }
            else if(e==10)
            {
                ten++;
                if(--five<0)
                    return false;
            }
            else if(e==20)
            {
                twenty++;
                //10+5 && 5+5+5 都不可以才找零失败
                int tmp1 = ten,tmp2 = five,tmp3 = five;
                if(--tmp1>=0&&--tmp2>=0)
                {
                    --ten;
                    --five;
                }
                else if((tmp3-=3)>=0)
                {
                    five-=3;
                }
                else
                    return false;
            }
        }
        return true;
    }
};

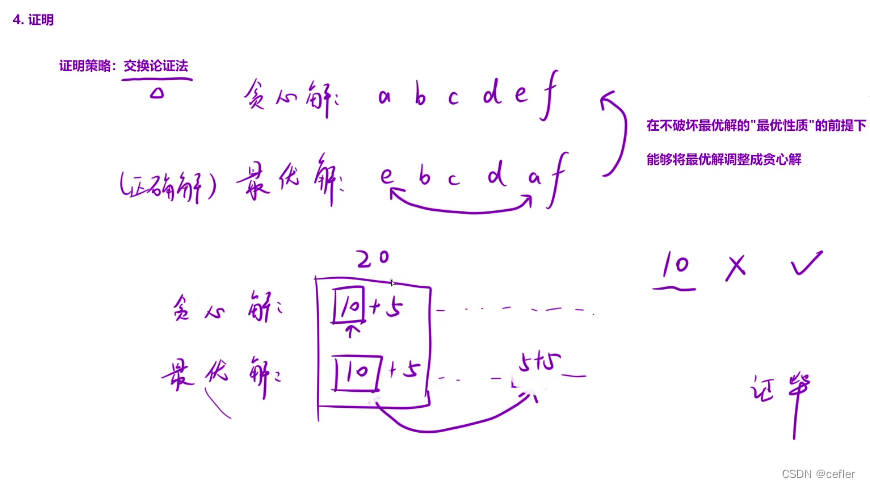
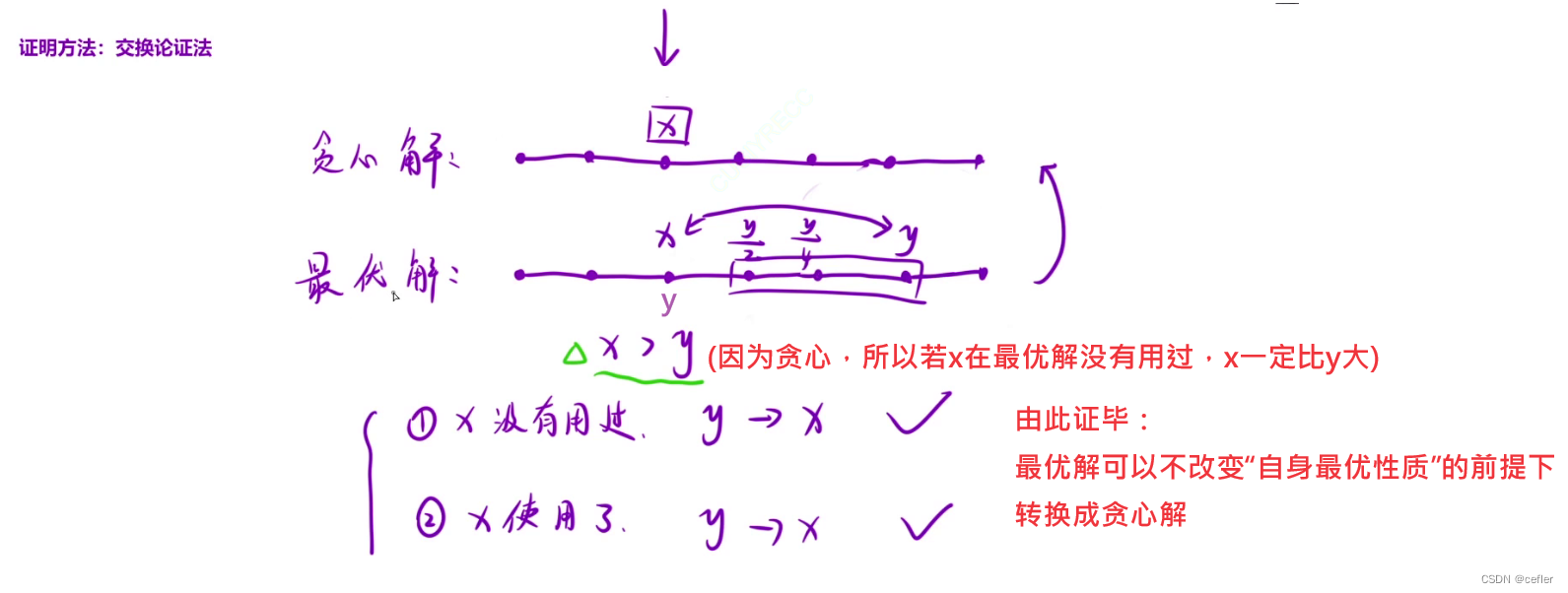
证明

交换论证法：

👉🏻将数组和减半的最少操作次数

原题链接：将数组和减半的最少操作次数

mycode:

class Solution {
public:
    int halveArray(vector<int>& nums) {
        priority_queue<double> heap;//默认大堆
        double sum = 0.0;
        for(auto e:nums)
        {
            heap.push(e);
            sum+=e;
        }
        sum/=2.0;
        int count = 0;
        while(sum>0)
        {
            double t = heap.top()/2.0;
            heap.pop();
            sum-=t;
            count++;
            heap.push(t);
        }
        return count;
    }
};

证明

priority_queue

当涉及到按照特定顺序处理元素时，C++ 的 std::priority_queue 是一个非常有用的容器适配器。它是一个基于堆的数据结构，用于实现优先级队列。在优先级队列中，元素按照其优先级被处理，具有较高优先级的元素先被处理。

以下是 std::priority_queue 的基本特征和用法：

包含头文件

#include <queue>

创建优先级队列

std::priority_queue<int> pq;  // 创建一个默认的最大堆

插入元素

pq.push(10);
pq.push(5);
pq.push(20);

访问顶部元素

int topElement = pq.top();  // 获取最高优先级的元素，但不删除

删除顶部元素

pq.pop();  // 删除最高优先级的元素

自定义比较函数
如果你想要自定义元素的比较方式，可以通过提供自定义比较函数来实现。以下是一个示例，创建一个最小堆：

#include <functional>

std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;

或者，你也可以自定义比较函数：

struct Compare {
    bool operator()(int a, int b) {
        // 自定义比较逻辑，返回 true 表示 a 的优先级高于 b
        return a > b;
    }
};

std::priority_queue<int, std::vector<int>, Compare> customQueue;

注意事项

• 默认情况下，std::priority_queue 是一个最大堆，但你可以通过提供第三个参数（比较函数）来改变其行为。
• std::priority_queue 不提供迭代器访问元素的方式，因为堆不是线性结构。
• 在使用自定义比较函数时，确保比较函数是严格弱序（strict weak ordering），以确保正确的行为。

👉🏻最大数

原题链接：最大数

mycode:

class Solution {
public:
    string largestNumber(vector<int>& nums) {
        vector<string> v;
        for(auto e:nums)
        {
            v.push_back(to_string(e));
        }
        //给v排序
        sort(v.begin(),v.end(),[](const string& s1,const string& s2)->bool
        {
            return s1+s2>s2+s1;
        }
        );
        string ret;
        for(auto e:v)
        {
            ret+=e;
        }
        if(ret[0]=='0')return "0";
        return ret;
    }
};

证明贪心策略：
这里即证明为什么这里可以排序

👉🏻摆动序列

原题链接：摆动序列

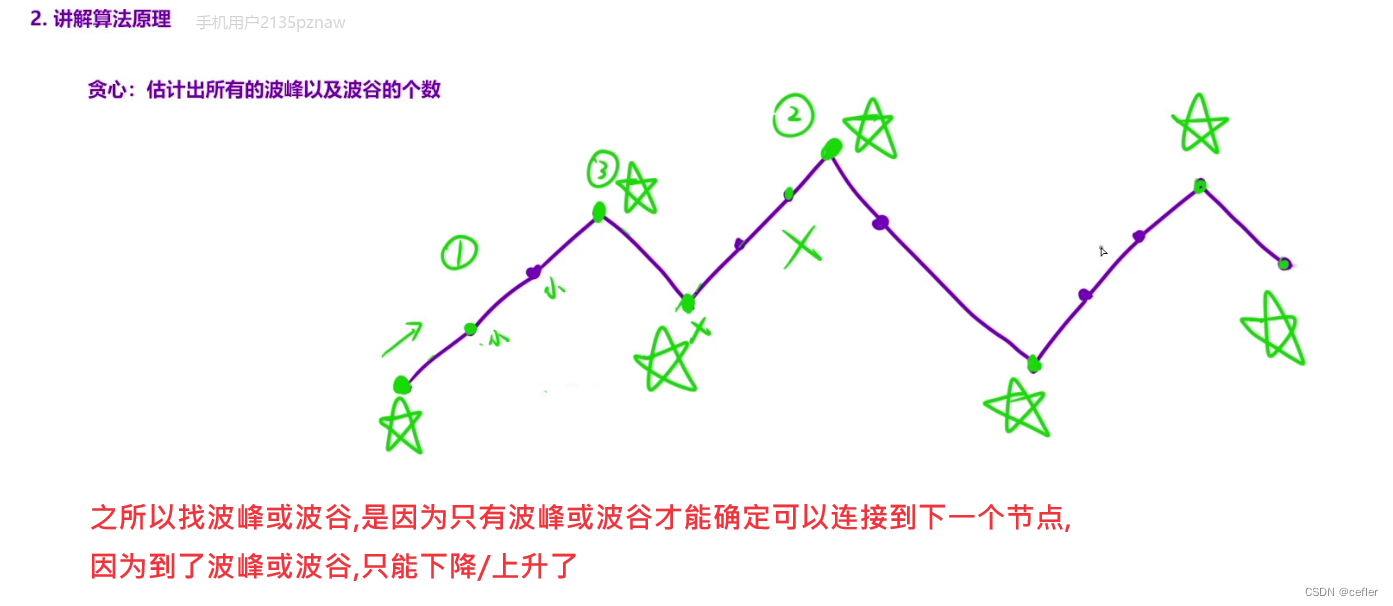
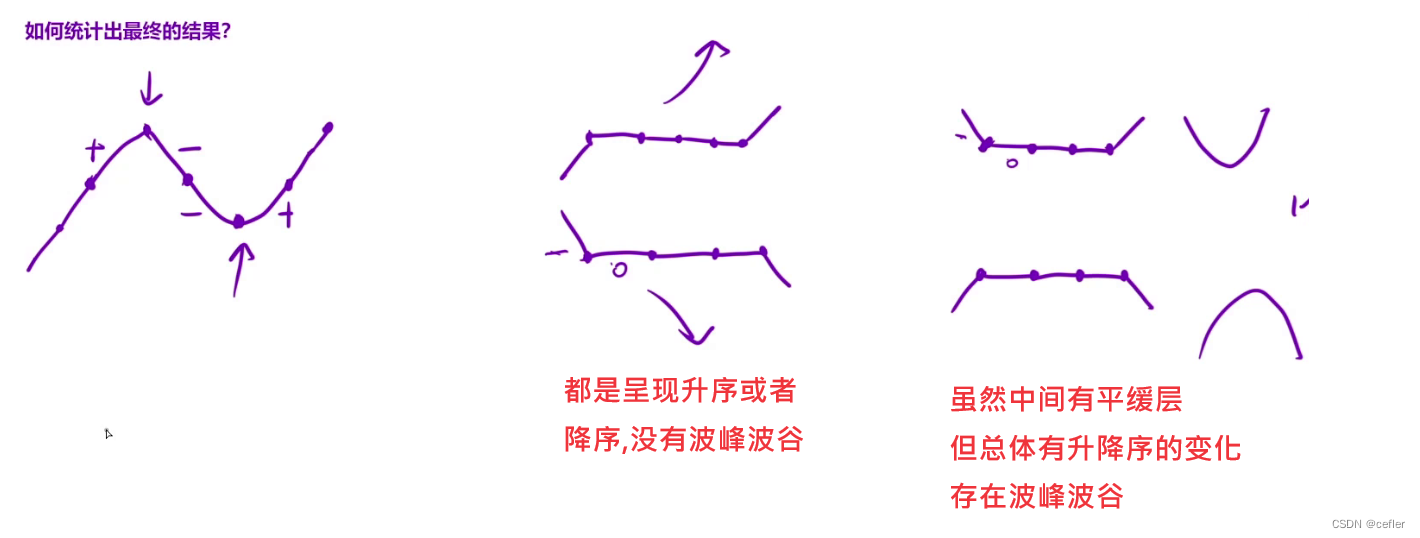
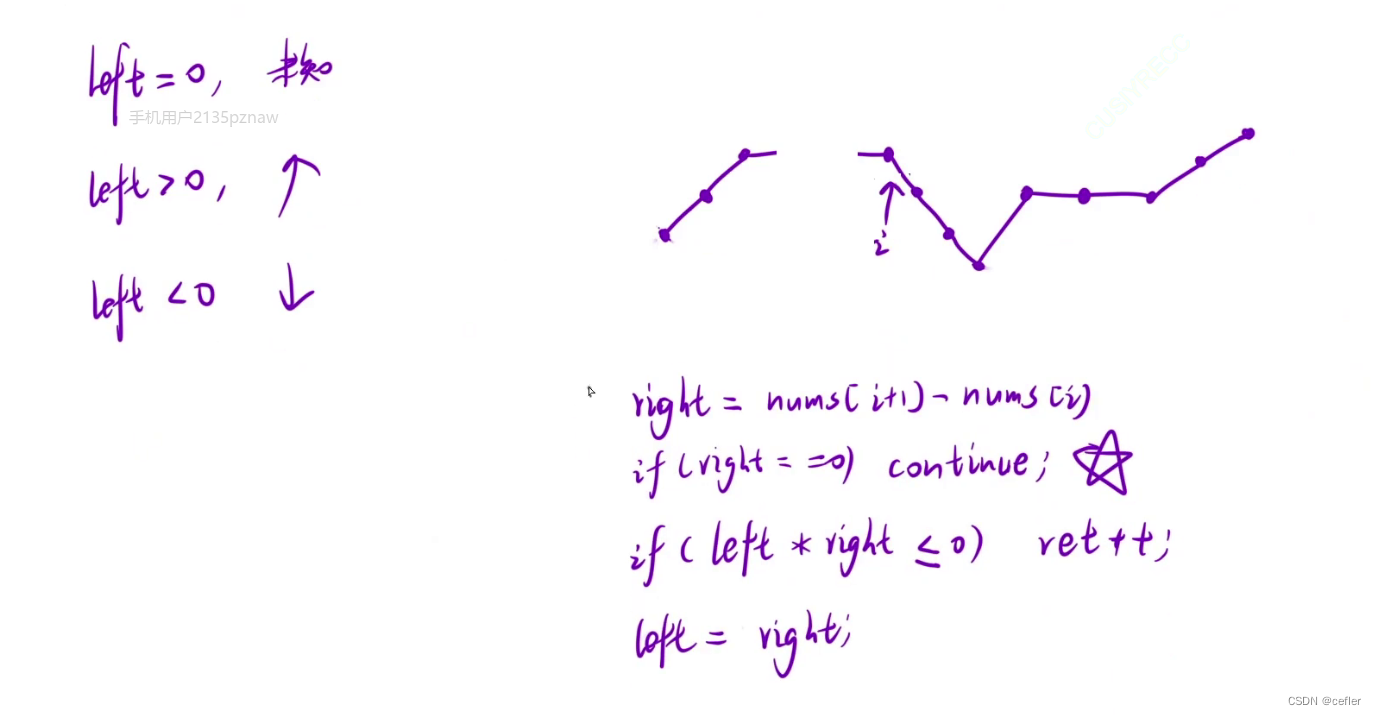
mycode:

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int count = 0;
        int left = 0;//左峰,=0未知升降序
        int right;//右峰
      for(int i = 0;i<nums.size()-1;i++)
      {
        right = nums[i+1]-nums[i];
        if(right == 0)
            continue;
        if(left*right<=0)//出现波峰或波谷了
        {
            count++;
        }
        left = right;
      }
      return count+1;
    }
};

证明贪心策略：

👉🏻最长递增子序列

原题链接：最长递增子序列
贪心策略:

• 在存放长度为x的元素时，只存放递增子序列长度为x的元素中x值最小的元素
• 存哪里（该元素位置的递增子序列最长长度是？）：假设该元素为num,去存放长度的数组中遍历对比，直到遇到大于等于num的元素或为空，前者的话将原元素覆盖取而代之，后者则直接入住即可
  
  

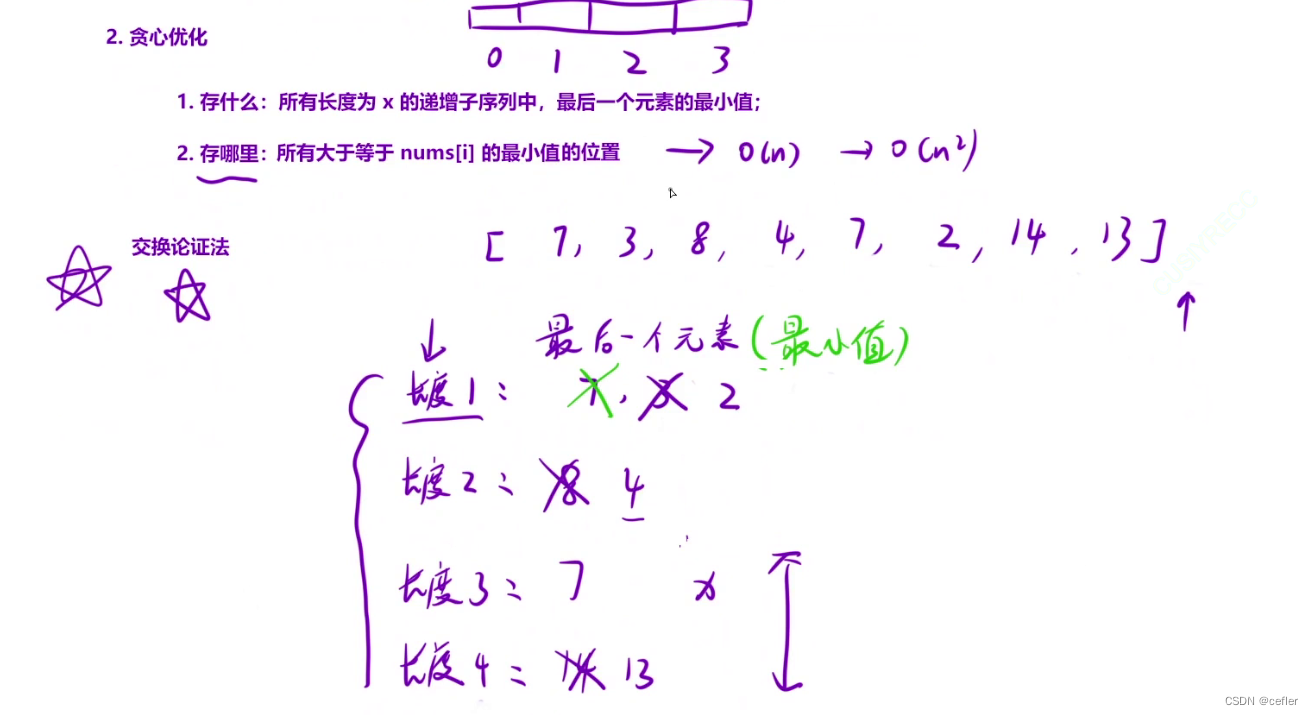
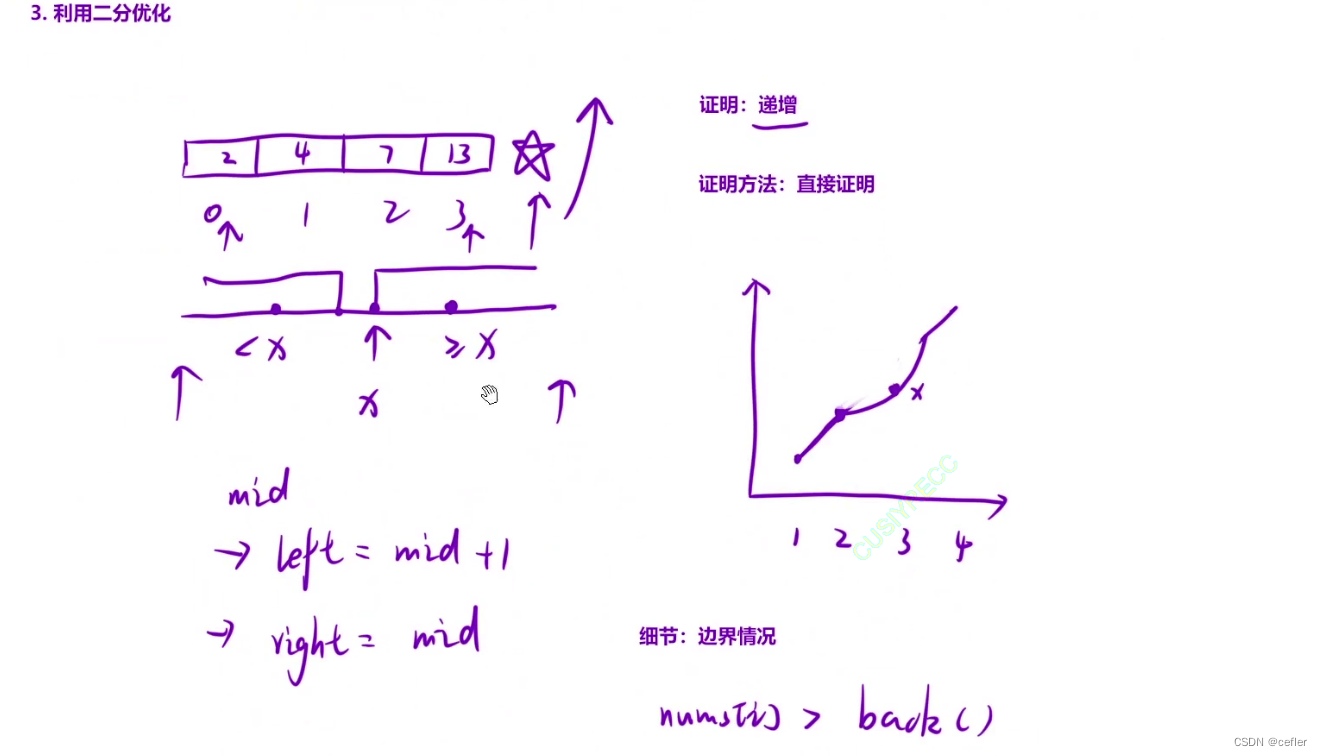
二分优化帮助num快速定位到自己位于哪个长度的位置

mycode(贪心做法)：

class Solution {
public:
    void binaryInsert(vector<int>& length,int num)
    {
        //特殊情况，若num大于nums中最大数值，则直接插入
        if(num>length.back()) 
        {
            length.push_back(num);
            return;
        }
        int left = 0,right = length.size()-1;
        int mid;
        while(left<right)
        {
            mid = (left+right)/2;
            if(length[mid]<num)
                left = mid+1;
            else 
                right = mid;
        }
        length[left] = num;//此时left == right,所以无论哪个都行
    }
    int lengthOfLIS(vector<int>& nums) {
        vector<int> length(1,nums[0]);//先存入第一个，然后从位置2开始遍历
        for(int i = 1;i<nums.size();i++){
            binaryInsert(length,nums[i]);
        }
        return length.size();
    }
};

mycode(动态规划)：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        //动态规划做法,状态表示dp[i]:第i个位置最长递增子序列长度
        //dp[i] = max(dp[j]+1)(j<i&&nums[j]<nums[i])
        int n = nums.size();
        //创建dp表并且初始化
        vector<int> dp(n,1);

        int ret = 1;
        for(int i = 1;i<n;i++)
        {
            for(int j = 0;j<i;j++)
            {
                if(nums[j]<nums[i])
                {
                    dp[i] = max(dp[j]+1,dp[i]);
                }
            }
            ret = max(dp[i],ret);
        }   
      return ret;
    }
};

👉🏻递增的三元子序列

原题链接：递增的三元子序列

mycode:

class Solution {
public:
void binaryInsert(vector<int>& length,int num)
    {
        //特殊情况，若num大于nums中最大数值，则直接插入
        if(num>length.back()) 
        {
            length.push_back(num);
            return;
        }
        int left = 0,right = length.size()-1;
        int mid;
        while(left<right)
        {
            mid = (left+right)/2;
            if(length[mid]<num)
                left = mid+1;
            else 
                right = mid;
        }
        length[left] = num;//此时left == right,所以无论哪个都行
    }

    bool increasingTriplet(vector<int>& nums) {
        vector<int> length(1,nums[0]);//先存入第一个，然后从位置2开始遍历
        for(int i = 1;i<nums.size();i++){
            binaryInsert(length,nums[i]);
            if(length.size()>=3)return true;
        }
        return false;

    }
};

贪心代码优化：动态数组

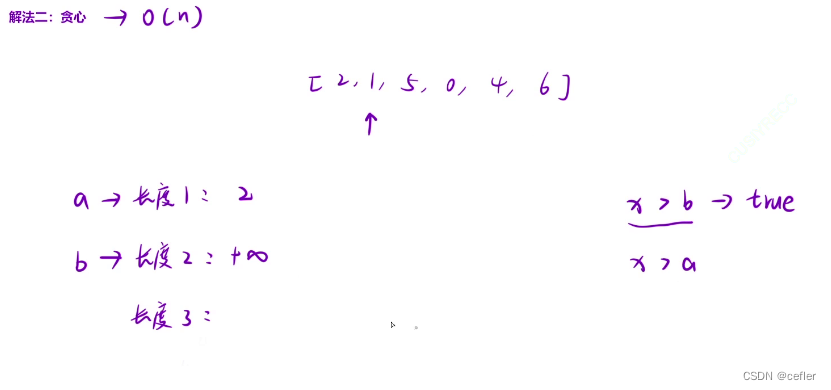
用两个变量a,b。初始化：a是nums数组的首元素，b设为INT_MAX
从数组第二个元素开始遍历，

• 如果大于b,则插入新元素，此时长度满足3 return true
• 小于a,则替换掉a
• 大于a小于b，则替换掉b

mycode:

class Solution {
public:
    bool increasingTriplet(vector<int>& nums) {
        int a = nums[0],b = INT_MAX;
        for(int i = 1;i<nums.size();i++)
        {
            if(nums[i]>b) return true;
            else if(nums[i]<a) a = nums[i];
            else if(nums[i]>a&&nums[i]<b) b = nums[i];
        }
        return false;
    }
};

👉🏻最长连续递增序列

原题链接：最长连续递增序列

mycode:

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int maxlen = 1;
        int len = 1;
        for(int i = 1;i<nums.size();i++)
        {
            if(nums[i]>nums[i-1]) len++;
            else
            {
                len = 1;//重新置为1
            }
            if(len>maxlen) maxlen = len;
        }
        return maxlen;
    }
};