二叉树中的深搜

原创已于 2023-12-28 17:47:32 修改 · 507 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#递归、回溯、深搜

于 2023-12-24 16:38:23 首次发布

递归、搜索与回溯专栏收录该内容

6 篇文章

订阅专栏

本文介绍了如何在编程中处理布尔二叉树，包括计算其值、求根节点到叶节点数字之和、二叉树剪枝、验证二叉搜索树、查找第K小的元素以及获取所有路径的方法。

在这里插入图片描述

👉🏻计算布尔二叉树的值

原题链接：计算布尔二叉树的值

mycode:

class Solution {
public:
    
    bool evaluateTree(TreeNode* root) {
        if(root->left==nullptr)
        {
            if(root->val==0)
                return false;
            else 
                return true;
        }
        else 
        {
            bool left = evaluateTree(root->left);
            bool right = evaluateTree(root->right);
            if(root->val==2)
                return left||right;
            else 
                return left&&right;
        }
    }
};

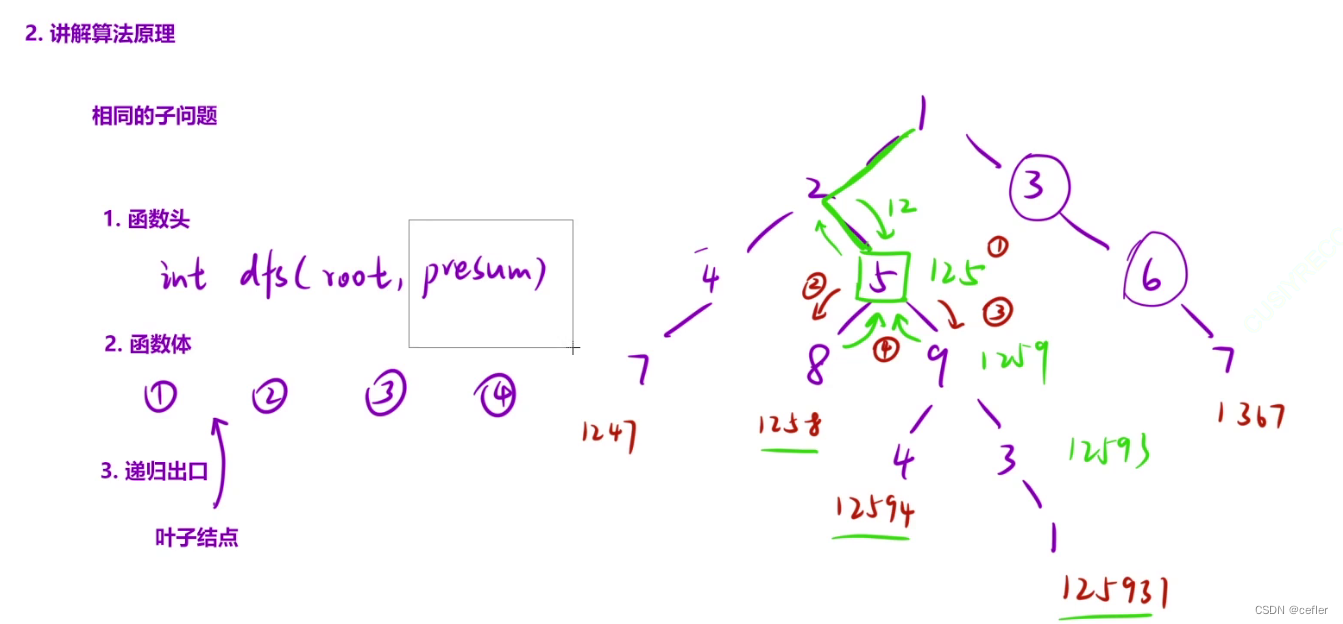
👉🏻求根节点到叶节点数字之和

原题链接：求根节点到叶节点数字之和

mycode:

class Solution {
public:
    int sumNumbers(TreeNode* root) {
        if(root==nullptr)return 0;

        return dfs(root,0);
    }
    int dfs(TreeNode* root,int presum){
        if(root==nullptr)return 0;
        presum=(presum*=10)+root->val;
        if(root->left==nullptr&&root->right==nullptr)
            return presum;
        int leftsum = dfs(root->left,presum);
        int rightsum = dfs(root->right,presum);

        return leftsum+rightsum;
    }
};

在这里插入图片描述

👉🏻二叉树剪枝

原题链接：二叉树剪枝

mycode:

class Solution {
public:
    TreeNode* pruneTree(TreeNode*& root) {
        //后序遍历
        if(root==nullptr)
            return nullptr;
        TreeNode* left = pruneTree(root->left);
         TreeNode* right = pruneTree(root->right);
        if(root->val==0&&left==nullptr&&right==nullptr)
            root=nullptr;
        
        return root;
            
    }
};

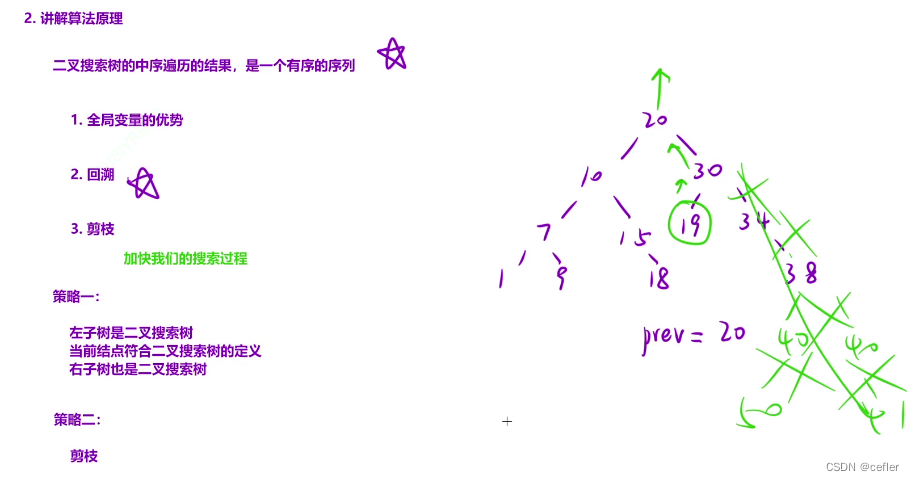
👉🏻验证二叉搜索树

原题链接：验证二叉搜索树

mycode:
在这里插入图片描述

class Solution {
public:
  long prev = LONG_MIN;
    bool isValidBST(TreeNode* root) {

        if(root==nullptr) return true;
        bool left = isValidBST(root->left);
        bool cur = false;
        if(root->val>prev)
            cur = true;
        prev = root->val;
        bool right = isValidBST(root->right);

        return left&&right&&cur;
    }

};

剪枝版本：

class Solution {
public:
  long prev = LONG_MIN;
    bool isValidBST(TreeNode* root) {

        if(root==nullptr) return true;
        bool left = isValidBST(root->left);
        if(left==false) return false;//剪枝
        bool cur = false;
        if(root->val>prev)
            cur = true;
       if(cur==false) return false;//剪枝
        prev = root->val;
        bool right = isValidBST(root->right);

        return left&&right&&cur;
    }

};

👉🏻二叉搜索树中第K小的元素

原题链接：二叉搜索树中第K小的元素

mycode:

class Solution {
public:
    int count;
    int ret;
    void dfs(TreeNode* root)
    {
        if(root==nullptr)return;
        dfs(root->left);
        --count;
        if(count==0)
        {
            ret = root->val;
            return;
        }
        dfs(root->right);
    }
    int kthSmallest(TreeNode* root, int k) {
      count = k;
      dfs(root);
      return ret;
    }
   
};

👉🏻二叉树的所有路径

原题链接：二叉树的所有路径

mycode:

class Solution {
public:
    vector<string> ret;
    void dfs(TreeNode* root,string s)
    {
        if(root==nullptr)return;
        if(root->left==nullptr&&root->right==nullptr) 
        {
            s+=to_string(root->val);
            ret.push_back(s);
            return;
        }
        s+=to_string(root->val);
 
        s+="->";
        dfs(root->left,s);
        dfs(root->right,s);

    }
    vector<string> binaryTreePaths(TreeNode* root) {
        string s;
        dfs(root,s);
        return ret;
    }
};