论文链接:https://ojs.aaai.org/index.php/AAAI/article/view/28707
研究背景:
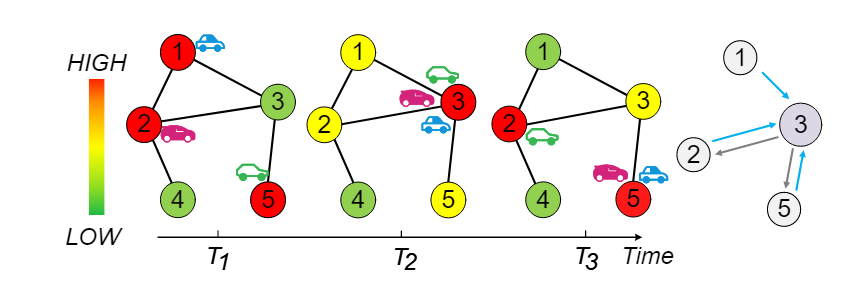
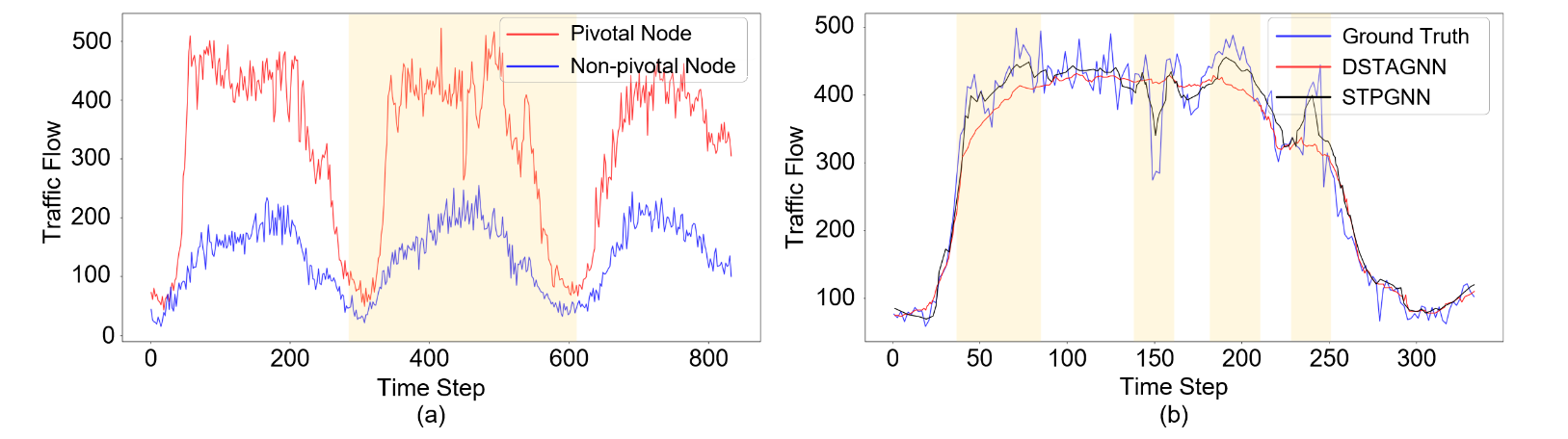
真实路网里存在少数枢纽节点(pivotal nodes):位置(如市中心、立交桥)或功能导致它们与很多节点有强耦合,表现为先“聚合”再”分配”流量(如通勤潮汐)。这类点的时空依赖更复杂、预测更难;多数方法对所有节点“一视同仁”,或只能用局部、简化的时空关系,因而难以抓住枢纽的关键作用。STPGNN的核心思想是:先找到枢纽,再围绕枢纽做精细的同步时空卷积,其他非枢纽仍用高效的图卷积+时间卷积,两路并行融合。
Notation:
路网图:
![]()
基于欧氏距离构建的邻接矩阵:
![]()
目标:学习函数F,用历史S步预测未来T步:
![]()
总体框架: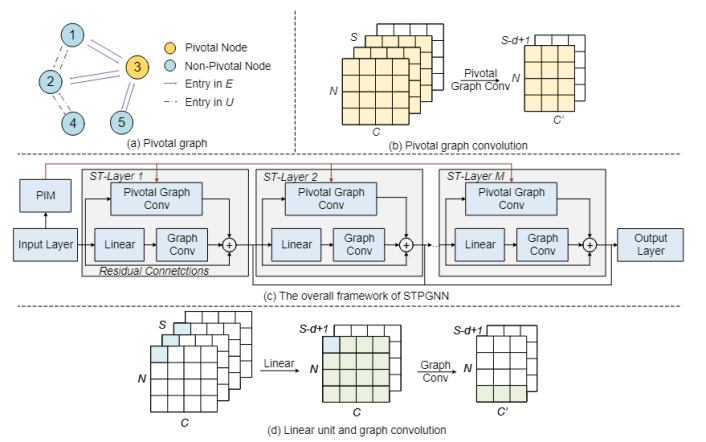
a.输入经过一层线性单元之后,进入PIM进行枢纽识别;
b.构造枢纽图;
c.堆积M个ST-Layer:每一层包含两条并行支路
1.PGCM(枢纽图卷积):在枢纽图上做时空卷积
2.GCN+Linear:在基础原图上对非枢纽做空间卷积+线性时间卷积
d.层间有残差,所有层的输出concat交给output(两次激活+两次线性卷积)
接下来我们分模块来分析
Module A: PIM
针对交通流问题中枢纽,直观的来讲可以从聚合和分配能力来定义。使用带时间偏移的相似度衡量从“j”到“i”的传播速度,再对行or列求和得到聚合和分配的能力,最后Top-K得到枢纽集合。
1.首先构造跨时相似度矩阵E
![]()
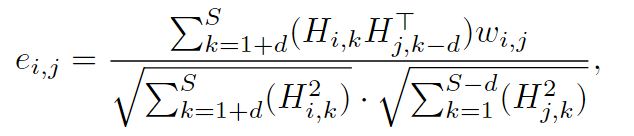
Wij是可学习的权重矩阵,公式含义是比较“i在当前步”与“j在d步前”的相似度,越大意味着“j到i的影响越强”。分子是带时间移动的相关性,分母是归一化操作。
2.然后进行枢纽打分和选择:
矩阵 E 的第 i 行的条目表示来自其他节点到 i 在时间 d 的节点依赖关系,因此矩阵 E 中每一行的总和产生流量图中每个节点的聚合能力的表示。类似地,矩阵 E 的第 i 列的总和可以表示节点 i 的分布能力。综合得分为:
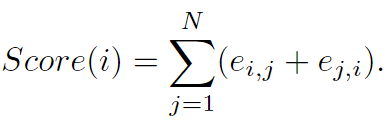
Top-K枢纽集合:
![]()
论文表明K=N/5时通常为最优。
3.枢纽图的邻接矩阵A
对涉及枢纽的边采用时移相似度并进行归一化,其余的边仍采用原始邻接矩阵U:
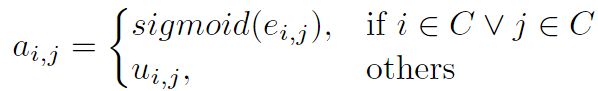
Module B: PGCM(枢纽)
时间和空间复杂度:普通的ST-GCN是在全图上考虑“时间×空间”的依赖,复杂度为O(TN^2);但是STPGNN将注意力集中在枢纽相关边上,这意味着它可以在不要求图拉普拉斯算子等谱滤波器的情况下将节点特征与其相邻节点融合,把复杂度降至O(TKN)。(K<<N)
张量的形状与卷积定义:
第l个ST-Layer输入H(l)把时间维度切成段:
![]()
同步时空卷积同步使用卷积核长为d的1D时间卷积并且使用A来聚合邻居:
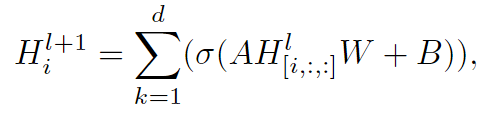
所谓时空同步体现在:每个时间位点 i 同时聚合最近d个时间切片与邻接矩阵A的空间邻居,实现同步。
Module C:Graph Conv+Linear Unit(非枢纽)
1.图卷积
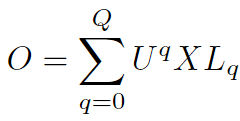
Lq为可学习参数,X为信号输入,O为输出。
2.线性单元层
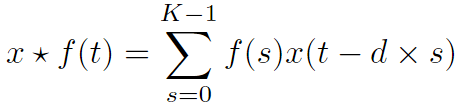
★代表卷积运算。
用U来抓空间、Linear Unit来抓时间;PGCM抓枢纽时空的同步关系,将两条路并行融合。
输出层与损失函数:
输出层:两次激活+两次线性卷积,汇聚M个ST-Layer的拼接特征,给出未来T步的预测。
损失函数MAE:
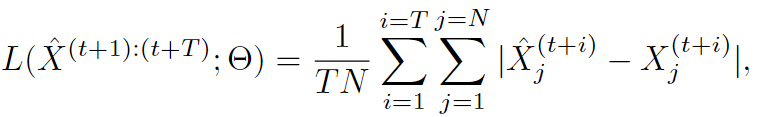
数据集:
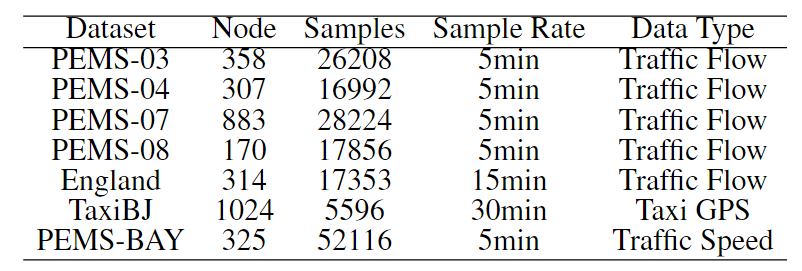
使用了PEMS、PEMS-BAY、England和TaxiBJ数据集。
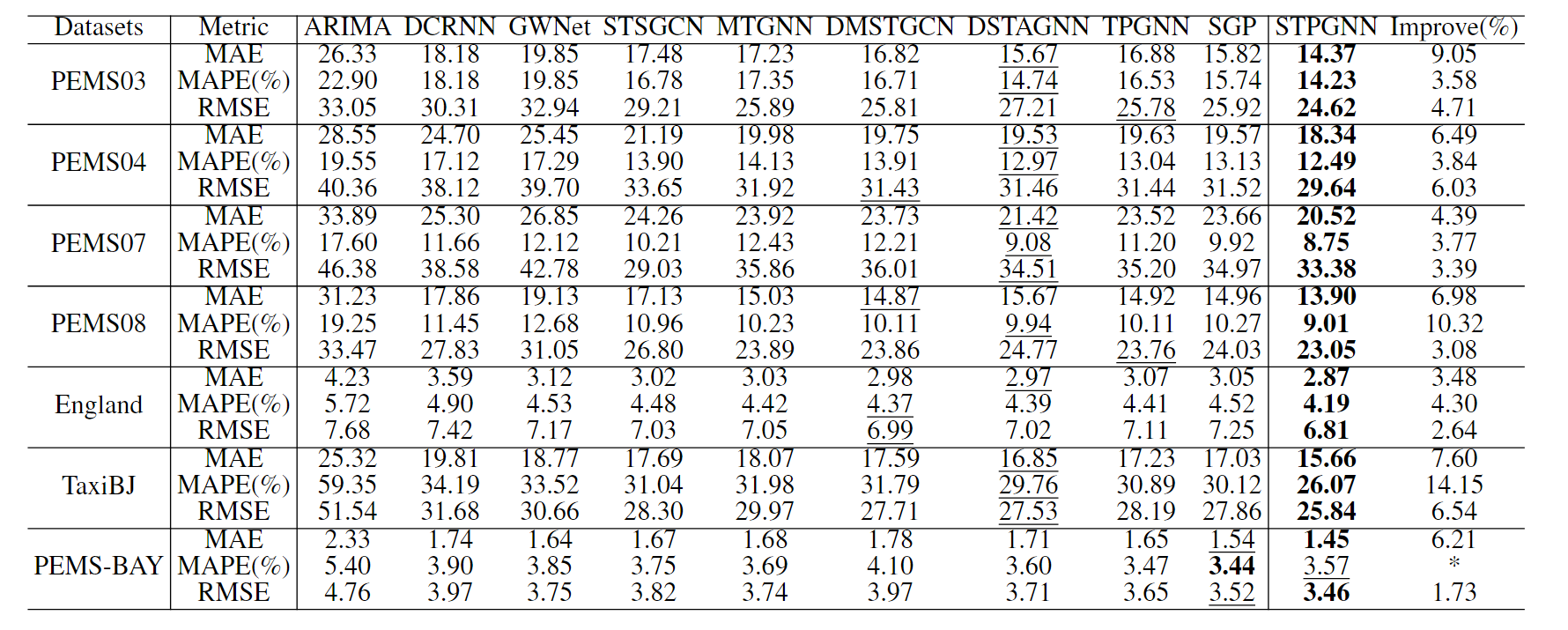
结果、性能分析:
总结:
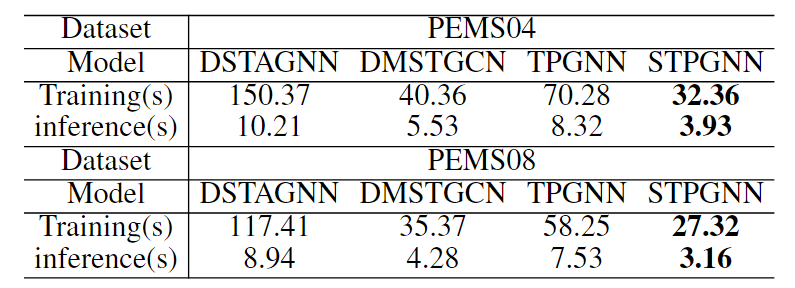
STPGNN 针对在全图上同步建模精确时空依赖会带来不可承受的时空复杂度的瓶颈,抓住路网中少数枢纽在汇聚与分发交通流上更复杂的客观现象:先以带时滞的相似度矩阵E同时度量每个节点的聚合/分发能力,经 Top-K 得分确定关键节点并据此把时序相关性显式注入到关键图邻接中,再用关键图卷积在该图上做同步时空卷积,将复杂度由 O(TdN2)降至 O(TdKN)而又不牺牲关键区域的刻画;与此同时,对非关键节点并行采用扩散式 GCN + 线性单元建模,层内融合输出,既保证精度又控制计算量。该框架在 PEMS03/04/07/08、PEMS-BAY、England、TaxiBJ 等七个数据集上多数指标优于强基线且训练推理更快;消融表明 PIM 与 PGCM 都是性能关键,且经验上 K≈N/5最优,从而在可解释性—效率—精度之间取得良好平衡。























 1135
1135










