四、Numpy

最新推荐文章于 2023-08-17 10:00:00 发布
原创 最新推荐文章于 2023-08-17 10:00:00 发布 · 316 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#numpy #机器学习 #人工智能

Numpy

1. Numpy介绍

1. 定义

开源的Python科学计算库，用于快速处理任意维度的数组。Numpy中，存储对象是ndarray

2. 创建

import numpy as np

score = np.array([[80, 89, 86, 67, 79],
                 [78, 97, 89, 67, 81],
                 [90, 94, 78, 67, 74],
                 [91, 91, 90, 67, 69],
                 [76, 87, 75, 67, 86],
                 [70, 79, 84, 67, 84],
                 [94, 92, 93, 67, 64],
                 [86, 85, 83, 67, 80]])

score

在这里插入图片描述

3. 优势

  1. 内存块风格 – 一体式存储

  2. 支持并行化运算

  3. 效率高于纯Python代码 – 底层使用了C，内部解除了GIL（全局解释器锁）

    import numpy as np
import random
import time

a = []
for i in range(1000000):
    a.append(random.random())

# 通过%time魔法方法，查看当前行的代码运行一次所花费的时间
%time sum1 = sum(a)

b = np.array(a)
%time sum2 = np.sum(b)

    在这里插入图片描述

2. N维数组 - ndarray

1. 属性

数组属性反映了数组本身固有的信息。

属性名字属性解释
ndarray.shape数组维度的元组
ndarray.ndim数组维数
ndarray.size数组中的元组数量
ndarray.itemsize一个数组元素的长度（字节）
ndarray.dtype数组元素的类型

2. 形状

import numpy as np

a = np.array([1, 2, 3])
a

# 输出结果
array([1, 2, 3])

import numpy as np

b = np.array([[1, 2, 3], [4, 5, 6]])
b

# 输出结果
array([[1, 2, 3],
       [4, 5, 6]])

import numpy as np

c = np.array([[[1,2,3], [4,5,6]], [[7,8,9],[10,11,12]]])
c

# 输出结果
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

import numpy as np

a = np.array([1, 2, 3])
a.shape

# 输出结果
(3,)

import numpy as np

b = np.array([[1, 2, 3], [4, 5, 6]])
b.shape

# 输出结果
(2, 3)

import numpy as np

c = np.array([[[1,2,3], [4,5,6]], [[7,8,9],[10,11,12]]])
c.shape

# 输出结果
(2, 2, 3)

import numpy as np

c = np.array([[[1,2,3], [4,5,6]], [[7,8,9],[10,11,12]]])
c.ndim

# 输出结果
3

3. 类型

dtype是numpy.dtype类型

名称描述简写
np.bool用一个字节存储的布尔类型（True或False）‘b’
np.int8一个字节大小，-128 ~ 127‘i’
np.int16整数，-32768 ~ 32767‘i2’
np.int32整数，-2^31 ~ 2^32 - 1‘i4’
np.int64整数，-2^63 ~ 2^63 - 1‘i8’
np.uint8无符号整数，0 ~ 255‘u’
np.uint16无符号整数，0 ~ 65535‘u2’
np.uint32无符号整数，0 ~ 2^32 - 1‘u4’
np.uint64无符号整数，0 ~ 2^64 - 1‘u8’
np.float16半精度浮点数：16位，正负号1位，指数5位，精度10位‘f2’
np.float32单精度浮点数：32位，正负号1位，指数8位，精度23位‘f4’
np.float64双精度浮点数：64位，正负号1位，指数11位，精度52位‘f8’
np.complex64复数，分别用两个32位浮点数表示实部和虚部‘c8’
np.complex128复数，分别用两个64位浮点数表示实部和虚部‘c16’
np.object_python对象‘O’
np.string_字符串‘S’
np.unicode_unicode类型‘U’
import numpy as np

a = np.array([1, 2, 3])
a.dtype

# 输出结果
dtype('int64')

import numpy as np

d = np.array([1, 2, 3], dtype=np.float32)
d

# 输出结果
dtype('float32')

import numpy as np

e = np.array(["a", "b", "c"], dtype=np.string_)
e

# 输出结果
array([b'a', b'b', b'c'], dtype='|S1')

3. 生成数组

1. 生成0和1的数组

  1. np.ones()
    import numpy as np

ones = np.ones([4, 8])
ones

# 输出结果
array([[1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.]])
  2. np.ones_like()
    import numpy as np

np.ones_like(zeros)

# 输出结果
array([[1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.]])
  3. np.zeros()
    import numpy as np

zeros = np.zeros([4, 8])
zeros

# 输出结果
array([[0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.]])
  4. np.zeros_like()
    import numpy as np

np.zeros_like(ones)

# 输出结果
array([[0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.]])

2. 从现有数组生成

  1. np.array

    import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
a

# 输出结果
array([[1, 2, 3],
       [4, 5, 6]])

  2. np.asarray

    import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
a2 = np.asarray(a) # 浅拷贝
a2

# 输出结果
array([[1, 2, 3],
       [4, 5, 6]])

  3. 关于array和asarray的不同

    • np.array：深拷贝
    • np.asarray：浅拷贝
    import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
a1 = np.array(a) # 深拷贝
a[0, 0] = 100
a1

# 输出结果
array([[1, 2, 3],
       [4, 5, 6]])

    import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
a2 = np.asarray(a) # 浅拷贝
a[0, 0] = 100
a2

# 输出结果
array([[100,   2,   3],
       [  4,   5,   6]])

3. 生成固定范围的数组

  1. np.linspace(start, stop, num, endpoint)：生成等间隔的序列
    • start：序列的起始值
    • stop：序列的终止值
    • num：要生成的等间隔样例数量，默认为50
    • endpoint：序列中是否包含stop值，默认为true
    import numpy as np
np.linspace(0, 100, 10)

# 输出结果
array([  0.        ,  11.11111111,  22.22222222,  33.33333333,
        44.44444444,  55.55555556,  66.66666667,  77.77777778,
        88.88888889, 100.        ])
  2. np.arange()：生成等间隔的数组
    import numpy as np

np.arange(10, 50, 2)

# 输出结果
array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42,
       44, 46, 48])
  3. np.logspace()：生成10^N
    import numpy as np

np.logspace(0, 2, 3)

# 输出结果
array([  1.,  10., 100.])

4. 生成随机数组

1. 使用模块

np.random模块

2. 均匀分布

  1. np.random.rand(d0, d1, ……, dn)
    • 返回[0.0, 1.0)内的一组均匀分布的数
    import numpy as np

np.random.rand(2, 3)

# 输出结果
array([[0.95502077, 0.68066242, 0.41043204],
       [0.58305373, 0.12350283, 0.31498541]])
  2. np.random.uniform(low=0.0, high=1.0, size=None)
    • 功能：从一个均匀分布[low,high)中随机采样，注意定义域是左闭右开，即包含low，不包含high。
    • low：采样下界，float类型，默认值为0；
    • high：采样上界，float类型，默认值为1；
    • size：输出样本数目，为int或元组类型，例如：size=(m,n,k)，则输出mnk个样本，缺省时输出1个值。
    • 返回值：ndarray类型，其形状和参数size中的描述一致。
    import numpy as np

np.random.uniform(1, 10, (3, 5))

# 输出结果
array([[7.66285421, 7.2512125 , 3.29511486, 1.70300794, 9.43636717],
       [7.58550077, 9.41953621, 3.30186123, 1.25149392, 4.71951143],
       [9.37364314, 7.68563467, 3.38919012, 6.2447495 , 8.0212071 ]])
  3. np.random.randint(low, high=None, size=None, dtype=‘l’)
    • 从一个均匀分布中随机采样，生成一个整数或N维整数数组，取数范围：若high不为None时，取[low, high)之间的随机整数，否则取值[0, low)之间随机整数。
    import numpy as np

np.random.randint(1, 10, (3, 5))

# 输出结果
array([[3, 3, 4, 8, 5],
       [6, 7, 2, 4, 2],
       [3, 4, 7, 8, 8]])
    • 使用均匀分布绘制直方图
    import numpy as np
import matplotlib.pyplot as plt

# 生成均匀分布的随机数
x1 = np.random.uniform(-1, 1, 1000000)

# 创建画布
plt.figure(figsize=(20, 8), dpi=100)

# 绘制直方图
plt.hist(x1, bins=1000) # x代表要使用的数据，bins表示要划分区间数

# 显示图像
plt.show()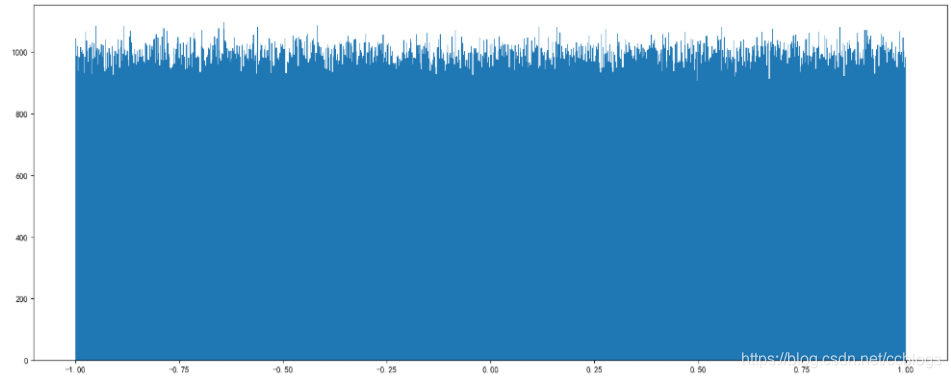
    在这里插入图片描述

3. 正态分布

  1. 均值（μ）：图形的左右位置
  2. 方差：图形是瘦，还是胖
    • 值越小，图形越瘦高，数据越集中
    • 值越大，图形越矮胖，数据越分散
  3. μ决定了其位置，其标准差σ决定了分布的程度。当μ = 1，σ = 1时的正态分布是标准正态分布。
    f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x - \mu)^2}{2\sigma^2}} f(x)=σ2π ​1​e−2σ2(x−μ)2​
  4. 方差与方差
    • 在概率论和统计方差衡量一组数据时离散程度的度量
      s 2 = ( x 1 − M ) 2 + ( x 2 − M ) 2 + ( x 3 − M ) 2 + ⋯ + ( x n − M ) 2 n s^2 = \frac{(x_1 - M)^2 + (x_2 - M)^2 + (x_3 - M)^2 + \cdots + (x_n - M)^2}{n} s2=n(x1​−M)2+(x2​−M)2+(x3​−M)2+⋯+(xn​−M)2​
    • M为平均值，n为数据总个数，S为标准差，S^2可以理解一个整体为方差
      σ = 1 N ∑ i = 1 N ( x i − μ ) 2 \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^N(x_i - \mu)^2} σ=N1​i=1∑N​(xi​−μ)2 ​
  5. 标准差与方差的意义
    • 可以理解成数据的一个离散程度的度量
  6. 创建方式
    • np.random.randn(d0, d1, ……, dn)：从标准正态分布中返回一个或多个样本值
    • np.random.normal(loc=0.0, scale=1.0, size=None)
      • loc：float，此概率分布的均值（对应着整个分布的中心centre）
      • scale：float，此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，越小，越瘦高）
      • size：int or tuple of ints，输出的shape，默认为None，只输出一个值
    • np.random.standard_normal(size=None)：返回指定形状的标准正态分布的数组
  7. 正态分布绘制直方图
    import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布数据
x = np.random.normal(1.75, 1, 100000)

# 创建画布
plt.figure(figsize=(20, 8), dpi=100)

# 绘制直方图
plt.hist(x, bins=1000) # x代表要使用的数据，bins表示要划分区间数

# 显示图像
plt.show()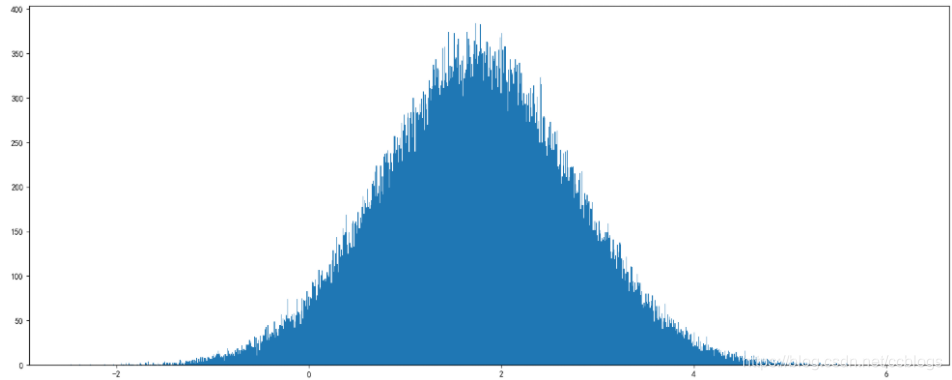
    在这里插入图片描述

5. 数组索引、切片

  1. 直接索引
    • 先进行行索引，再进行列索引
    import numpy as np

stock_change = np.random.normal(0, 1, (8, 10))
stock_change[0:2, 0:3] # 前两行，前三列

# 输出结果
array([[-0.74707534,  0.19114589, -0.88483482],
       [-1.58156334,  1.00287796, -1.87640528]])
    • 高维数组索引，从宏观到微观
    # 多维数组的切片
import numpy as np

a1 = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
a1[1, 0, 2]

# 输出结果
9
  2. 形状修改
    • 对象(ndarray).reshape(shape[, order])
    import numpy as np

stock_change = np.random.normal(0, 1, (4, 5))
stock_change

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629, -0.69427984],
       [ 0.35946321, -0.73208893, -0.08400495,  0.05579022,  0.21873223],
       [-0.59769751,  0.61834508,  1.29287825, -0.73456679,  0.88735471],
       [-0.06548732, -0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])

#################
stock_change.reshape([5, 4])

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629],
       [-0.69427984,  0.35946321, -0.73208893, -0.08400495],
       [ 0.05579022,  0.21873223, -0.59769751,  0.61834508],
       [ 1.29287825, -0.73456679,  0.88735471, -0.06548732],
       [-0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])

#################
# 不设定行数，可以直接将行数设为-1，设定的列数必须能被个数整除，否则报错
stock_change.reshape([-1, 4])

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629],
       [-0.69427984,  0.35946321, -0.73208893, -0.08400495],
       [ 0.05579022,  0.21873223, -0.59769751,  0.61834508],
       [ 1.29287825, -0.73456679,  0.88735471, -0.06548732],
       [-0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])
    • 对象(ndarray).resize(new_shape[, refcheck])
    import numpy as np

stock_change

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629, -0.69427984],
       [ 0.35946321, -0.73208893, -0.08400495,  0.05579022,  0.21873223],
       [-0.59769751,  0.61834508,  1.29287825, -0.73456679,  0.88735471],
       [-0.06548732, -0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])

#################
stock_change.resize([5, 4]) # 不反回值，对本身变量进行更改
stock_change

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629],
       [-0.69427984,  0.35946321, -0.73208893, -0.08400495],
       [ 0.05579022,  0.21873223, -0.59769751,  0.61834508],
       [ 1.29287825, -0.73456679,  0.88735471, -0.06548732],
       [-0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])
    • 对象(ndarray).T：数组的转置(将数组的行、列进行互换)
    import numpy as np

stock_change

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629],
       [-0.69427984,  0.35946321, -0.73208893, -0.08400495],
       [ 0.05579022,  0.21873223, -0.59769751,  0.61834508],
       [ 1.29287825, -0.73456679,  0.88735471, -0.06548732],
       [-0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])

#################
stock_change.T

# 输出结果
array([[-0.41863679, -0.69427984,  0.05579022,  1.29287825, -0.12888261],
       [ 1.27702133,  0.35946321,  0.21873223, -0.73456679, -0.8411004 ],
       [ 0.54314808, -0.73208893, -0.59769751,  0.88735471,  0.76181773],
       [-0.19999629, -0.08400495,  0.61834508, -0.06548732, -0.44921914]])
  3. 类型修改
    • 对象(ndarray).astype(type)
    import numpy as np

stock_change

# 输出结果
array([[-0.41863679,  1.27702133,  0.54314808, -0.19999629],
       [-0.69427984,  0.35946321, -0.73208893, -0.08400495],
       [ 0.05579022,  0.21873223, -0.59769751,  0.61834508],
       [ 1.29287825, -0.73456679,  0.88735471, -0.06548732],
       [-0.12888261, -0.8411004 ,  0.76181773, -0.44921914]])

#################
stock_change.astype(np.int16)

# 输出结果
array([[0, 1, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 0],
       [1, 0, 0, 0],
       [0, 0, 0, 0]], dtype=int16)
    • 对象(ndarray).tostring([order])
    import numpy as np

str = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
str

# 输出结果
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

#################
str.tostring()

# 输出结果
b'\x01\x00\x00\x00\x00\x00\x00\x00\x02\x00\x00\x00\x00\x00\x00\x00\x03\x00\x00\x00\x00\x00\x00\x00\x04\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x06\x00\x00\x00\x00\x00\x00\x00\x07\x00\x00\x00\x00\x00\x00\x00\x08\x00\x00\x00\x00\x00\x00\x00\t\x00\x00\x00\x00\x00\x00\x00\n\x00\x00\x00\x00\x00\x00\x00\x0b\x00\x00\x00\x00\x00\x00\x00\x0c\x00\x00\x00\x00\x00\x00\x00'
  4. 数组去重
    • 对象(ndarray).unique
    import numpy as np

str = np.array([[1, 2, 3, 4, 5], [3, 4, 5, 6, 7]])
np.unique(str)

# 输出结果
array([1, 2, 3, 4, 5, 6, 7])
  5. 各行的列不对应
    import numpy as np

obj = np.array([[1, 2, 3], [4, 5]])
obj

# 输出结果
array([list([1, 2, 3]), list([4, 5])], dtype=object)

#################
obj.dtype

# 输出结果
dtype('O')

6. ndarray运算

1. 逻辑运算

import numpy as np

# 准备数据
stock_change = np.random.normal(0, 1, (8, 10))
stock_change

# 输出结果
array([[-2.12129471, -1.37690302, -1.27890702,  2.14513727, -0.33934842,
         0.37705686, -0.64305235, -0.78922556,  0.79498005, -0.86109014],
       [ 0.29991271,  0.85752293, -0.03512881,  1.02710926, -1.2563507 ,
         1.65498861, -0.58438326, -1.51988918, -0.09293134, -2.73519473],
       [-0.70361896,  1.31526884, -0.40599565, -2.04836896, -1.34679555,
        -0.21390926, -0.05396001,  0.67788869, -0.65001194,  0.73824703],
       [ 0.44158209, -0.03932038, -0.72056005,  0.23185009, -0.74720743,
        -0.0910574 ,  1.09114265, -0.03381264,  0.05549276, -0.66151873],
       [ 1.12680666,  0.21913315, -0.49581926,  0.05395026, -1.52248609,
         0.62104614,  0.66863118, -0.1292667 ,  0.04663375,  0.59474957],
       [-0.22758085,  1.06152583, -0.45115448,  2.90416263,  0.4970265 ,
         0.15877648, -0.43060429, -0.58815933, -1.57204304, -0.14493885],
       [-0.17280553,  0.39409815,  0.70118543,  0.77043511,  0.9202859 ,
         1.09209001,  0.00316529,  1.97606516, -0.00741256,  0.05749327],
       [ 0.41083613, -0.51700284, -1.45306175, -0.47917366,  1.97285277,
         0.15641835, -0.31635235,  0.75009645, -0.26490995, -1.3846922 ]])

#####################################
# 取五行五列
stock_c = stock_change[0:5, 0:5]
stock_c

# 输出结果
array([[-2.12129471, -1.37690302, -1.27890702,  2.14513727, -0.33934842],
       [ 0.29991271,  0.85752293, -0.03512881,  1.02710926, -1.2563507 ],
       [-0.70361896,  1.31526884, -0.40599565, -2.04836896, -1.34679555],
       [ 0.44158209, -0.03932038, -0.72056005,  0.23185009, -0.74720743],
       [ 1.12680666,  0.21913315, -0.49581926,  0.05395026, -1.52248609]])

#####################################
# 判断数组中的数据是否大于1
stock_c > 1

# 输出结果
array([[False, False, False,  True, False],
       [False, False, False,  True, False],
       [False,  True, False, False, False],
       [False, False, False, False, False],
       [ True, False, False, False, False]])

#####################################
# 将数组中大于1的数字设置为2
stock_c[stock_c > 1] = 2
stock_c

# 输出结果
array([[-2.12129471, -1.37690302, -1.27890702,  2.        , -0.33934842],
       [ 0.29991271,  0.85752293, -0.03512881,  2.        , -1.2563507 ],
       [-0.70361896,  2.        , -0.40599565, -2.04836896, -1.34679555],
       [ 0.44158209, -0.03932038, -0.72056005,  0.23185009, -0.74720743],
       [ 2.        ,  0.21913315, -0.49581926,  0.05395026, -1.52248609]])

2. 通用判断函数

import numpy as np

# 数据准备
stock_d = np.random.normal(0, 1, (2, 5))
stock_d

# 输出结果
array([[-1.90727062,  0.09562091, -0.08388499,  1.03427889,  0.66508996],
       [ 0.45467056, -0.69797447,  0.57751618,  0.24689873,  0.46118822]])

#####################################
# 全部满足条件才返回True
np.all(stock_d > 0)

# 输出结果
False

#####################################
# 只要一个满足条件就返回True
np.any(stock_d > 0)

# 输出结果
True

3. np.where（三元运算符）

  1. np.where
    import numpy as np

stock_d

# 输出结果
array([[-1.90727062,  0.09562091, -0.08388499,  1.03427889,  0.66508996],
       [ 0.45467056, -0.69797447,  0.57751618,  0.24689873,  0.46118822]])

#####################################
# 满足条件赋值为1，不满足条件赋值为0
np.where(stock_d > 0, 1, 0)

# 输出结果
array([[0, 1, 0, 1, 1],
       [1, 0, 1, 1, 1]])
  2. np.logical_and和np.logical_or
    import numpy as np

stock_d

# 输出结果
array([[-1.90727062,  0.09562091, -0.08388499,  1.03427889,  0.66508996],
       [ 0.45467056, -0.69797447,  0.57751618,  0.24689873,  0.46118822]])

#####################################
# 两个条件都满足返回0， 否则返回1
np.where(np.logical_and(stock_d < 0.5, stock_d > -0.5), 0, 1)

# 输出结果
array([[1, 0, 0, 1, 1],
       [0, 1, 1, 0, 0]])

#####################################
# 满足其中任何一个条件就返回1，否则返回0
np.where(np.logical_or(stock_d > 0.5, stock_d < -0.5), 1, 0)

# 输出结果
array([[1, 0, 0, 1, 1],
       [0, 1, 1, 0, 0]])

4. 统计运算

  1. min：最小值
  2. max：最大值
  3. median：中位数
  4. mean：均值
  5. std：标准差
  6. var：方差
  7. argmax：最大值下标
  8. argmin：最小值下标
import numpy as np

stock_d

# 输出结果
array([[-1.90727062,  0.09562091, -0.08388499,  1.03427889,  0.66508996],
       [ 0.45467056, -0.69797447,  0.57751618,  0.24689873,  0.46118822]])

#####################################
# 获取序列中的最大值
stock_d.max()

# 输出结果
1.0342788906045899

#####################################
# 按列获取序列中的最大值，有的API的axis=0是按列，有的是按行
stock_d.max(axis=0)

# 输出结果
array([0.45467056, 0.09562091, 0.57751618, 1.03427889, 0.66508996])

#####################################
# 按行获取序列中的最大值，有的API的axis=1是按行，有的是按列
stock_d.max(axis=1)

# 输出结果
array([1.03427889, 0.57751618])

#####################################
# 序列中的第一个最大值的索引值，也可以设置axis求行列的最大索引值
stock_d.argmax()

# 输出结果
3

#####################################
# 序列中的第一个最小值的索引值，也可以设置axis求行列的最小索引值
stock_d.argmin()

# 输出结果
0

7. 矩阵和向量

1. 矩阵

  1. 定义：matrix，和array的区别矩阵必须是2维的，但是array可以是多维的。矩阵的维数即行数乘以列数。 A i j A_{ij} Aij​指第i行第j列的元素。
    A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix} A=⎣⎡​135​246​⎦⎤​

2. 向量

  1. 定义：一种特殊的矩阵，讲义中的向量一般都是列向量，下面展示的就是三维列向量（3*1）
    A = [ 1 2 3 ] A = \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix} A=⎣⎡​123​⎦⎤​

3. 加法和标量乘法

  1. 矩阵的加法：行列数相等的可以加。
    [ 1 2 3 4 5 6 ] + [ 1 2 3 4 5 6 ] = [ 2 4 6 8 10 12 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix} + \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \\ 10 & 12 \\ \end{bmatrix} ⎣⎡​135​246​⎦⎤​+⎣⎡​135​246​⎦⎤​=⎣⎡​2610​4812​⎦⎤​
  2. 矩阵的乘法：每个元素都要承。
    3 ∗ [ 1 2 3 4 5 6 ] = [ 3 6 9 12 15 18 ] 3 * \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix} = \begin{bmatrix} 3 & 6 \\ 9 & 12 \\ 15 & 18 \\ \end{bmatrix} 3∗⎣⎡​135​246​⎦⎤​=⎣⎡​3915​61218​⎦⎤​

4. 矩阵向量乘法

  1. 算法：m * n的矩阵乘以n * 1的向量，得到的是m * 1的向量。
    [ 1 3 4 0 2 1 ] ∗ [ 1 5 ] = [ 16 4 7 ] 1 ∗ 1 + 3 ∗ 5 = 16 4 ∗ 1 + 0 ∗ 5 = 4 2 ∗ 1 + 1 ∗ 5 = 7 ( M 行 , N 列 ) ∗ ( N 行 , L 列 ) = ( M 行 , L 列 ) \begin{array}{l} \begin{bmatrix} 1 & 3 \\ 4 & 0 \\ 2 & 1 \\ \end{bmatrix} * \begin{bmatrix} 1 \\ 5 \\ \end{bmatrix} = \begin{bmatrix} 16 \\ 4 \\ 7 \\ \end{bmatrix} \\ \\ 1 * 1 + 3 * 5 = 16 \\ 4 * 1 + 0 * 5 = 4 \\ 2 * 1 + 1 * 5 = 7 \\ \\ (M行, N列) * (N行, L列) = (M行, L列) \end{array} ⎣⎡​142​301​⎦⎤​∗[15​]=⎣⎡​1647​⎦⎤​1∗1+3∗5=164∗1+0∗5=42∗1+1∗5=7(M行,N列)∗(N行,L列)=(M行,L列)​

5. 矩阵乘法

  1. 算法：(M行, N列) * (N行, L列) = (M行, L列)
    [ A 0 A 1 A 2 A 3 ] ∗ [ B 0 B 1 B 2 B 3 ] = [ C 0 C 1 C 2 C 3 ] A 0 ∗ B 0 + A 1 ∗ B 2 = C 0 A 0 ∗ B 1 + A 1 ∗ B 3 = C 1 A 2 ∗ B 0 + A 3 ∗ B 2 = C 2 A 2 ∗ B 1 + A 3 ∗ B 3 = C 3 \begin{array}{l} \begin{bmatrix} A_0 & A_1 \\ A_2 & A_3 \\ \end{bmatrix} * \begin{bmatrix} B_0 & B_1 \\ B_2 & B_3 \\ \end{bmatrix} = \begin{bmatrix} C_0 & C_1 \\ C_2 & C_3 \\ \end{bmatrix} \\ \\ A_0 * B_0 + A_1 * B_2 = C_0 \\ A_0 * B_1 + A_1 * B_3 = C_1 \\ A_2 * B_0 + A_3 * B_2 = C_2 \\ A_2 * B_1 + A_3 * B_3 = C_3 \\ \end{array} [A0​A2​​A1​A3​​]∗[B0​B2​​B1​B3​​]=[C0​C2​​C1​C3​​]A0​∗B0​+A1​∗B2​=C0​A0​∗B1​+A1​∗B3​=C1​A2​∗B0​+A3​∗B2​=C2​A2​∗B1​+A3​∗B3​=C3​​

6. 矩阵乘法的性质

  1. 矩阵乘法不满足交换律：A * B ≠ B * A
  2. 矩阵的乘法满足结合律：A * (B * C) = (A * B) * C
  3. 单位矩阵：从左上角到右下角的对角线上的元素均为1，以外全是0的矩阵。一般用I或者E来表示。
    [ 1 0 0 1 ] \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} [10​01​]

7. 逆、转置

  1. 矩阵的逆：如矩阵A是一个M*M矩阵（方阵），逆矩阵：AA-1= A-1A = I
  2. 低阶矩阵求逆的方法
    1. 待定系数法
    2. 伴随矩阵
    3. 初等变换
  3. 矩阵的转置：设A为m * n阶矩阵，第i行j列的元素为A=a(i, j)。定义A转置为n * m的矩阵B，满足B=a(j, i)，即b(i, j) = a(j, i)，记AT = B。

8. 数组间运算

1. 数组与数的运算

import numpy as np

arr = np.array([1, 2, 3, 4])
arr

# 输出结果
array([1, 2, 3, 4])

#####################################
arr + 1

# 输出结果
array([2, 3, 4, 5])

#####################################
arr / 2

# 输出结果
array([0.5, 1. , 1.5, 2. ])

#####################################
arr * 10

# 输出结果
array([10, 20, 30, 40])

2. 数组与数组的运算（需要满足广播机制）

执行broadcast的前提在于，连能个ndarray执行的是element-wise的运算，Broadcast机制的功能是为了方便不同形状的ndarray（numpy库的核心数据结构）进行数学运算。

当操作两个数组时，numpy会逐个比较它们的shape（构成的元组tuple），只有在下述情况下，两个数组才能够进行数组与数组的运算。

  • 维度相等
  • shape（其中相对应的一个地方为1）
Image(3d array)： 256 * 256 * 3
Scale(1d array)：             3
Result(3d array)：256 * 256 * 3

A (4d array)：    9 * 1 * 7 * 1
B (3d array)：        8 * 1 * 5
Result(4d array)：9 * 8 * 7 * 5

A (2d array)：    5 * 4
B (1d array)：        1
Result(2d array)：5 * 4

A (3d array)：    15 * 3 * 5
B (3d array)：    15 * 1 * 1
Result(3d array)：15 * 3 * 5

import numpy as np

arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1], [3]])
arr1 + arr2

# 输出结果
array([[2, 3, 4, 3, 2, 5],
       [8, 9, 4, 5, 6, 4]])

9. 矩阵运算

1. 矩阵乘法api：

  • np.matmul - 矩阵相乘
    import numpy as np

a = np.array([[80, 86], [82, 80], [85, 78], [90, 90],
              [86, 82], [82, 90], [78, 80], [92, 94]])
b = np.array([[0.7], [0.3]])
np.matmul(a, b)

# 输出结果
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])
  • np.dot - 点乘
    import numpy as np

a = np.array([[80, 86], [82, 80], [85, 78], [90, 90],
              [86, 82], [82, 90], [78, 80], [92, 94]])
b = np.array([[0.7], [0.3]])
np.dot(a, b)

# 输出结果
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

#####################################
np.dot(a, 10)

# 输出结果
array([[800, 860],
       [820, 800],
       [850, 780],
       [900, 900],
       [860, 820],
       [820, 900],
       [780, 800],
       [920, 940]])
  • 比较：两者之间进行矩阵相乘时没有区别，但是dot支持矩阵与数字相乘。
07-08 numpy字符串处理（增删改+判断函数）
weixin_46400833的博客
07-08 1026
一、numpy字符串处理 1、numpy提供char模块处理字符串，运用向量化运算方式； 2、char模块提供常用的字符串函数，如连接，切片，删除，替换等； 具体如下： numpy里边的函数对数据的处理 比 Python中循环处理数据高效很多 所有经过numpy处理的数据返回的都是array类型； char模块的函数有： ① upper() --字符大写化 str_list=['Hello','World'] python: [ i.upper for i in str_list] numpy:
Python之数据分析（Numpy的使用、多维数组、数据类型）
Viewinfinitely的博客
07-06 1172
文章目录写在前面一、数据分析与Numpy二、多维数组三、Numpy的数据类型 写在前面 代码中的np表示的是numpy，因为导入的时候是：import numpy as np 一、数据分析与Numpy 1、数据分析 MATLAB：专业化数据分析工具 Numpy：更简单上手，且结合了MATLAB大部分功能 2、Numpy介绍 应用于数值分析领域的Python语言工具 是一个开源的科学计算库 弥补了作为通用编程语言的Python在数值计算方面能力弱、速度慢的不足 拥有丰富的数学函数、强大的多位数组和优异的运算
Python numpy基础上
yuyuyuliang00的博客
08-17 680
本文介绍了numpy中最重要的概念，数组的相关知识。包括数组的数据类型，以及各类常用的创建方式(zeros, ones, linspace, random,eye)。此处主要介绍的是numpy数组的基本操作。提取子数组。创建数组副本数组变形拼接和拆分本篇主要介绍了numpy数组的通用计算方法，通用计算把数组元素循环的复杂度封装起来。本片介绍最常用的聚合计算；集合计算通常用于数据进行处理和分析，以及实现高级的数据分析算法。
Numpy数据类型
cd_sywe的博客
03-13 931
NumPy数据类型 类型类型代码说明int8、uint8i1、u1有符号和无符号8位整型（1字节）int16、uint16i2、u2有符号和无符号16位整型（2字节）int32、uint32i4、u4有符号和无符号32位整型（4字节）int64、uint64i8、u8有符号和无符号64位整型（8字节）float16f2半精度浮点数float32f4、f单精度浮点数float64f8、d双精度浮点数float128f16、g扩展精度浮点数complex64c8分别用两个32位表示的复数complex128c1
Numpy的简单介绍
qq_42413820的博客
06-14 608
Array(数组)》rank 数组的维数import numpy as npa = np.array([1,2,3])a.shape  #(3,)  明确指定a的维数  a = a.reshape((1,-1)) , 其中-1是个占位符，不表示任何意义a.shape  #(1,3)np.ones(),np.zeros()函数均可由full()函数替代    a = np.full((3,3),0)...
numpy基础知识样例运用
chen_zan_yu_的博客
01-07 615
#导入 numpy的包 import numpy as np #输出numpy的版本 np.__version__ # numpy 是有序的 数据类型相同的集合 # numpy 优先级 str>float>int #[434,'434',True] # numpy的数组 # 可以通过dtype=float 指定转化类型 np.array([344.56,324,9843,4343,'45'],dtype=float) （数字后面的点代表浮点数） np.ar.
numpy
01-20
视频本质上是一系列连续的图片，可以理解为四维数组。 8. **计算机视觉**： 对于图像和视频的深度处理，`opencv-python`库是常用的工具，它可以读取、处理和分析图像和视频。`cv2`是`opencv-python`的导入别名，...
numpy-2.0.0.tar.gz
最新发布
06-29
四、在深度学习中的应用 在深度学习中，Numpy是构建神经网络模型的基础，主要用于： 1. **数据预处理**：Numpy可以方便地对图像、声音等数据进行预处理，如归一化、标准化等。 2. **权重初始化**：在创建模型时，...
numpy - numpy tutorial
06-23
#### 四、NumPy数据类型 NumPy支持多种数据类型，这些类型通过`dtype`对象表示。 - **Data Type Objects (dtype)**：用于定义数组中的元素类型。例如，可以通过`np.dtype('int32')`来定义一个32位整数的数据类型。...
numpy中文手册
03-16
**四、数值计算** 1. **基本数学函数**: numpy提供了许多基本数学函数，如`sin()`, `cos()`, `exp()`, `log()`, `sqrt()`等，可以应用于整个数组。 2. **统计函数**: 包括`sum()`, `mean()`, `median()`, `std()`,...
Numpy进阶
12-21
在Numpy这个强大的Python数值...以上四个知识点是Numpy进阶操作的重要组成部分，它们可以帮助开发者更高效地处理多维数据，实现复杂的数据分析任务。掌握这些技巧，能显著提升你在数据科学和机器学习项目中的工作效率。
NumPy 矩阵处理
热门推荐
Bluebelfast的专栏
01-08 2万+
NumPy 是 Numerical Python 的简称，是高性能计算和数据分析的基础包。本书中几乎所有高级工具都是建立在它的基础之上，下面是它所能做的一些事情： ndarray，快速和节省空间的多维数组，提供数组化的算术运算和高级的 广播 功能。使用标准数学函数对整个数组的数据进行快速运算，而不需要编写循环。读取/写入磁盘上的阵列数据和操作存储器映像文件的工具。线性代数，随机数生成
Numpy数据类型对象（dtype）
呆码
01-30 2万+
常用方法 #记住引入numpy时要是用别名np，则所有的numpy字样都要替换 #查询数值类型 &gt;&gt;&gt;type(float) dtype('float64') # 查询字符代码 &gt;&gt;&gt; dtype('f') dtype('float32') &gt;&gt;&gt; dtype('d') dtype('float64') # 查询双字符代码 &gt;&gt...
numpy基础属性方法随机整理（一 附加）---类型字符码
酱紫煲饭~
06-22 850
类型字符码表 类型 字符码 布尔 ？ 有符号字节 b 无符号字节 B 整型 i / i2 / i4 / i8 (i8: int64) 无符号整形 u/ u2 / u4 / u8 浮点数 f2 / f4 / f8 (f8: float64) 复数 c8 / c16 (c8: complex64)...
NumPy学习笔记
DawnRanger的专栏
11-11 7343
1. 简介Numeric Python的简称，是几乎所有python科学计算工具的基础。主要功能： ndarray: 一个具有矢量运算和复杂广播能力的快速并且节省空间的多维数组 面向数组的运算: 对于数组进行快速运算的标准数学函数 磁盘读写、内存映射 线性代数、随机数、傅里叶变换 NumPy本身并没有提供什么高级的数据分析能力，但是理解NumPy数组以及面向数组的计算将有利于使用pandas等工具。
【利用Python进行数据分析】4 NumPy基础
小狐狸
03-01 3221
NumPy（Numerical Python的简称）是Python数值计算最重要的基础包。大多数提供科学计算的包都是用NumPy的数组作为构建基础。 NumPy的部分功能如下： ndarray，一个具有矢量算术运算和复杂广播能力的快速且节省空间的多维数组。 用于对整组数据进行快速运算的标准数学函数（无需编写循环）。 用于读写磁盘数据的工具以及用于操作内存映射文件的工具。 线性代数、随机数生成以及...
Numpy数据类型及数组创建01
数据攻城狮的博客
03-08 1638
文章目录1.常量numpy.nannumpy.infnumpy.pinumpy.e2.数据类型3.时间日期和时间增量4.数组的创建 1.常量 numpy.nan 1.表示空值。 2.nan = NaN = NAN 【例】两个numpy.nan是不相等的。 import numpy as np print(np.nan == np.nan) # False print(np.nan != np.nan) # True 在IDLE里执行失败，在Jupyter Notebook里执行成功 numpy.is
NumPy基础：数组的运算
qq_48657881的博客
02-17 834
NumPy⽤户称其为⽮量化（vectorization）。⼤⼩相等的数组之间的任何算术运算都会将运算应⽤到元素级： In [51]: arr = np.array([[1., 2., 3.], [4., 5., 6.]]) In [52]: arr Out[52]: array([[ 1., 2., 3.], [ 4., 5., 6.]]) In [53]: arr * arr Out[53]: array([[ 1., 4., 9.], [ 16., 25., 36.]]) 数组与标量的算术运算会将标量
Numpy 使用详解
一个程序员的成长之路。。。
09-17 1046
Numpy 概述： 是基于向量化的运算 进行数值运算时Numpy数组比list效率高 用于读写硬盘上基于数组的数据集的工具 线性代数运算、傅里叶变换,以及随机数生成 用于将C、C++、Fortran代码集成到Python的工具 除了为Python提供快速的数组处理能力，NumPy在数据分析方面还有另外一个主要作用,即作为在算法之间传递数据的容器。 NumPy的ndarray 创建ndarray
numpy 四维数组
09-11
numpy四维数组是指具有四个维度的数组。根据引用中的解释，我们可以将四维数组的结构理解为：第一维度中有2个元素，第二维度中有2个二维数组，第三维度中有2个一维数组，最里面一层的一维数组中有3个元素。这样的结构可以表示为：[2, 2, 2, 3]。也就是说，numpy四维数组中的每个元素都由四个索引值确定。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值