代码随想录算法训练营第二天 | LeetCode977.有序数组的平方，209.长度最小的子数组，59.螺旋矩阵II

最新推荐文章于 2026-01-08 22:28:34 发布

原创最新推荐文章于 2026-01-08 22:28:34 发布 · 1.2k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #矩阵 #线性代数

本文介绍了LeetCode中的三个算法问题：有序数组的平方、长度最小的子数组（滑动窗口）和螺旋矩阵II。通过双指针和滑动窗口技巧优化了解题效率，提供了C++代码示例和视频讲解链接。

代码随想录算法训练营第二天 | LeetCode977.有序数组的平方，209.长度最小的子数组，59.螺旋矩阵II

前言

今天的内容依旧为对数组进行操作

一、977.有序数组的平方

题目描述：
给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

另外还有提示如下：

1 <= nums.length <= 1e4
-1e4 <= nums[i] <= 1e4
nums 已按 非递减顺序 排序

题目建议：
本题关键在于理解双指针思想

暴力解题思路：
刚看到题目，会首先想到暴力解法，即遍历数组把每个元素先平方，然后将数组排序，得到答案数组。

暴力解题代码C++：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int t = nums.size();
        
        for(int i = 0; i < t; i ++)
            nums[i] = nums[i] * nums[i];
        
        sort(nums.begin(), nums.end());
        
        return nums;
    }
};

双指针解题思路：
根据题意我们可以知道，数组其实是有序的，只不过负数平方之后可能成为最大数了。那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。此时可以考虑双指针法了，i指向起始位置，j指向终止位置。从两边开始遍历数组，建立一个和原数组空间大小一样的res数组从尾部向头部存储，每次两个指针对应元素平方的值的较大值。
双指针方法的时间复杂度为O(n)，较暴力做法O(nlogn)快。

双指针解题代码C++：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int t = nums.size();
        vector<int> res(t, 0);
        
        int i = 0, j = t - 1, k = t - 1;
        while(i <= j)
        {
            if(nums[i] * nums[i] >= nums[j] * nums[j])
            {
                res[k --] = nums[i] * nums[i];
                i ++;
            }
            else
            {
                res[k --] = nums[j] * nums[j];
                j --;
            }
        }
        
        return res;
    }
};

文章讲解：https://programmercarl.com/0977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.html
视频讲解：
https://www.bilibili.com/video/BV1QB4y1D7ep

二、209.长度最小的子数组

题目描述：
给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2:
输入：target = 4, nums = [1,4,4]
输出：1

示例 3:
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

另外还有提示如下：

1 <= target <= 1e9
1 <= nums.length <= 1e5
1 <= nums[i] <= 1e5

题目建议：
本题关键在于理解滑动窗口，这个滑动窗口看文字讲解还挺难理解的，建议大家先看视频讲解。拓展题目可以先不做。

暴力解题思路：
这道题目暴力解法当然是用两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2)。不过现在leetcode更新了数据，用暴力做法会超时！

暴力解题代码C++：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {

        int res = nums.size() + 1;

        for(int i = 0; i < nums.size(); i ++)
        {
            int sum = 0;
            for(int j = i; j < nums.size(); j ++)
            {
                sum += nums[j];
                if(sum >= target)
                {
                    res = min(res, j - i + 1);
                    break;
                }
            }
        }

        if(res == nums.size() + 1) return 0;
        else return res;
    }
};

双指针解题思路：
在这里插入图片描述

1.窗口就是满足其和 ≥ s 的长度最小的连续子数组。
2.窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
3.窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。
4.滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

双指针解题代码C++：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {

        int res = nums.size() + 1, sum = 0;

        int i = 0;
        for(int j = 0; j < nums.size(); j ++)
        {
            sum += nums[j];
            while(sum >= target)
            {
                res = min(res, j - i + 1);
                sum -= nums[i ++];
            }
        }

        if(res == nums.size() + 1) return 0;
        else return res;
    }
};

文章讲解：https://programmercarl.com/0209.%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.html
视频讲解：
https://www.bilibili.com/video/BV1tZ4y1q7XE

三、59.螺旋矩阵II

题目描述：
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
`
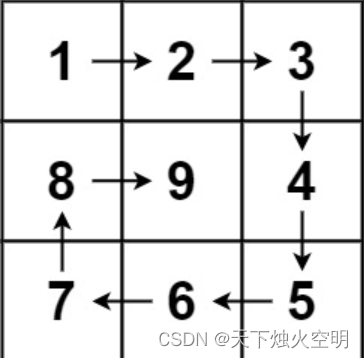
在这里插入图片描述

示例 1:
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2:
输入：n = 1
输出：[[1]]

另外还有提示如下：

1 <= n <= 20

题目建议：
本题关键还是在转圈的逻辑，在二分搜索中提到的区间定义，在这里又用上了。

解题思路：
做法参考AcWing756. 蛇形矩阵
因为在给数组赋值的过程中，要涉及“拐弯”，于是乎我们设置了4个偏移量，分别对应向上，向右，向下，向左，当遍历数组越界的时候，我们将偏移量的值加在当前元素行列坐标上，实现“拐弯”的操作。

解题代码C++：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        
        vector<vector<int>> res(n, vector<int>(n)); 
        
        int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
        for(int x = 0, y = 0, d = 0, k = 1; k <= n * n; k ++)
        {
            res[x][y] = k;
            int a = x + dx[d], b = y + dy[d];
            
            if(a < 0 || a >= n || b < 0 || b >= n || res[a][b])
            {
                d = (d + 1) % 4;
                a = x + dx[d], b = y + dy[d];
            }
            
            x = a, y = b;
        }
        
        return res;
    }
};