一. 泛型算法
1. 前言
泛型算法:可以支持多种类型的算法
此处主要来讨论怎么使用标准库中定义的泛型算法<algorithm>, numeric, ranges. 在引入泛型算法之前,还有一种是方法的形式,比如说std::sort 和std::list::sort,前者是算法,后者是list类中定义的函数(方法)
为什么引入泛型算法,而不用方法的形式?
- c++内建数据类型不支持方法(如int,float等,vector可以)
- 计算逻辑存在相似性,避免重复定义
但如果有方法和泛型算法同名,功能类似时,建议使用方法,比如std::find和std::map::find,即只要类里面提供了这个方法就使用,因为一般这个类中的方法可以针对此类有更好的优化。
2. 泛型算法的分类
读:给定迭代空间,读其中的元素并进行计算。举例:std::accumulate, std::find, std::count
写:向一个迭代区间中写入元素,一定要保证写入的目标区间的大小足够(后续也会提到怎么给目标区间动态扩充)。 举例:
- 单纯写:
std::fill(直接给结果idx),std::fill_n(给的count数) - 读+写:
std::transform(一般可以对一个vector做某种运算后存入新vector),std::copy
排序:改变输入序列中元素的顺序。举例:std::sort,std::unique(去除相邻的重复元素,使用前需要对数组进行排序,且会把重复的元素放到数组的最后面,这个用于区分的索引是unique的返回值,可以之后erase掉)
3. 迭代器的种类*(catagory)
*了解即可,和迭代器的类型不同,比如int*可以作为一种类型。一般,根据不同的迭代器种类,会有不同的优化算法
- 输入迭代器:可读,可递增
- 输出迭代器:可写,可递增
- 前向迭代器:可读写,可递增
- 双向迭代器:可读写,可递增递减
- 随机访问迭代器:可读写,可递减一个整数
4. 特殊迭代器
-
插入迭代器:back_insert_iterator, front_insert_iterator, insert_iterator
-
流迭代器: istream_iterator, ostream_iterator
#include <iterator> #include <sstream> int main() { std::istringstream str("1 2 3 4 5"); std::istream_iterator<int> x(str); std::istream_iterator<int> y{}; //流迭代器中,用此表示结束 for(; x!=y; ++x) { std::cout << *x << std::endl; //可以依次打印出12345 } }#include<vector> #include <iterator> #include <numeric> #include <sstream> int main() { std::vector<int> x{1,2,3,4,5}; std::copy(x.rbegin(), x.rend(), std::ostream_iterator<int>(std::cout, " ")); //打印结果为”5 4 3 3 1 “ } -
反向迭代器
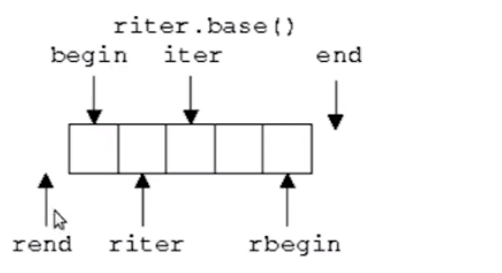
-
移动迭代器:move_iterator
5.并发算法
std::execution::seq 顺序执行
std::execution::par 并发执行
std::execution::par_unseq 并发非顺序执行
std::execution::unseq
二. bind和lambda表达式
1. 可调用对象
类似于sort算法中,用来定义sort规则的那个部分
- 函数指针:概念直观但定义位置受限
- 类:功能强大但书写麻烦
- bind:基于已有的逻辑灵活适配,但复杂逻辑时语法会难懂
- lambda:小巧灵活,功能强大
2. bind
早期的bind1st和bind2nd
#include <functional>
bool MyPredict(int val)
{
return val >3;
}
int main()
{
std::vector<int> x{1,2,3,4,5,6,7,8,9,10};
std::vector<int> y;
std::copy_if(x.begin(), x.end(), std::back_inserter(y), std::bind1st(std::greater<int>(), 3)); //打印出的为1,2
std::copy_if(x.begin(), x.end(), std::back_inserter(y), std::bind2nd(std::greater<int>(), 3)); //打印出的为4,5,6,7,8,9,10
for(auto p : y)
{
std::cout << p << ' ';
}
std::cout << std::endl;
}
变为bind:
通过绑定的方式修改可调用对象的调用方式
MyPredict(int val1, int val2)
{
return val1 > val2;
}
bool MyAnd(bool val1, bool val2)
{
return val1&& val2;
}
int main()
{
using namespace std::placeholders;
auto x = std::bind(MyPredict2, _1, 3); //按照上一块代码的内容打印出4-10的数字
x(50); //50是调用MyPredict2时出啊内的第1个参数,对应MyPredict函数中的val1,会判断50>3是否成立,返回true
auto y = std::bind(MyPredict2, 3, _1); //3对应val1的数值,而_1就是调用时写的第一个参数,比如y(4),那么val2就是4,相当于判断3>4是否成立,此处返回false。即只有当数字小于3时,返回值才是true
auto z = std::bind(MyPredict2, _2, _1);
std::cout << z(3,4); //返回1,4对应val1,3对应val2
auto x1 = std::bind(MyPredict2, _1, 3);
auto x2 = std::bind(MyPredict2, 10, _1);
auto x3 std::bind(MyAnd, x1, x2);
std::cout << x3(5); // 返回true,因为满足10>5 && 5>3
bind的使用风险
在调用std::bind(c++11引入)时,传入的参数会被赋值,这可能产生一些调用风险,可以使用std::ref或则和std::cref避免复制的行为。c++20之后,std::bind_front是std::bind的简化形式
#include <iostream>
#incldue <algorithm>
#include <vector>
#include <functional>
#include <memory>
void MyProc(int* ptr)
{
}
void MyProc(std::shared_ptr<int> ptr)
{
}
auto fun()
{
int x;
return std::bind(MyProc, &x); //风险1:返回了一个bind构造的可调用对象,但其内部包含了一个int型的指针,这个指针指向的一个局部的对象,有风险
}
auto fun2()
{
std::shared_ptr<int> x(new int());
return std::bind(MyProc, x); //OK, 因为堆上会分配一块内存,然后会把内存拷贝进去
}
void Proc(int& x)
{
++x;
}
int main()
{
//风险1
auto ptr = fun();
ptr(); //这个行为就是未定义的
int x=0;
auto b = std::bind(Proc, x); //绑定
b(); //实际执行
std::cout << x << std::endl;
//风险2
int x = 0;
Proc(x);
std::cout << x << std::endl; //打印结果为1
x=0;
auto ptr = std::bind
auto b = std::bind(Proc, x); //绑定
b(); //实际执行
std::cout << x << std::endl; //打印结果为0。 因为在调用bind的时候,x还是会复制一份再去处理,传递给Proc的是复制后的x',被修改的是x'
auto b = std::bind(Proc, std::ref(x)); //std::ref会生成一个对象,这个对象也会拷贝给bind,但是拷贝出的对象内部会包含一个引用来引用x,所以还是可以修改x的数值;std::cref()表示常量引用
}
bind_front用例:默认绑定到第一个元素
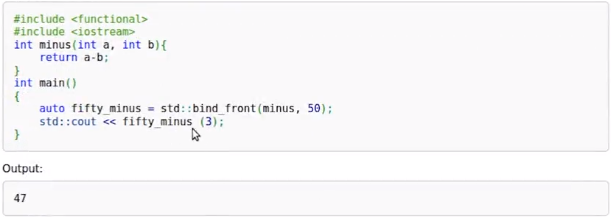
3. lambda表达式
为了更灵活的实现可调用对象而引入,从c++11开始在持续更新中
lambda表达式等效为一个类的对象6,主要内容包括以下几个点:
- 参数和函数体
- 返回类型
- 捕获:针对函数体中使用的局部自动对象进行捕获
- 说明符:mutable, constexpr, consteval
- 模板形参
//一般可以用auto自动推导出返回类型
auto x = [](int val)
{
return (val > 3.0) && val < 15.0);
}; //不要忘记这里的分号
//这里return的一个是float,一个是double,所以必须要指定返回类型
auto x = [](int val) ->float
{
if (val > 3)
{
return 3.0;
}
else
{
return 1.5f;
}
}; //不要忘记这里的分号
//捕获, 这样才可以把局部自动y传递到lambda表达式里面
//如果是静态变量or全局变量就不需要捕获可以直接使用
int y = 10;
auto x = [y](int val)
{
return val >y;
}; //不要忘记这里的分号
//捕获, 这样才可以把局部自动y传递到lambda表达式里面
int y = 10;
auto x = [y](int val) mutable
{
++y; //这里用了mutable,只有值捕获,y在lambda表达式内的操作不会影响到外部
return val >y;
}; //不要忘记这里的分号
std::cout << y << std::endl; //输出的y的值是10.
//捕获, 这样才可以把局部自动y传递到lambda表达式里面
int y = 10;
auto x = [&y](int val)
{
++y; //这里用了引用捕获,y在lambda表达式内的操作会影响到外部
return val >y;
}; //不要忘记这里的分号
std::cout << y << std::endl; //输出的y的值是11.
//捕获, 这样才可以把局部自动y传递到lambda表达式里面
int y = 10;
int z = 3;
//中括号里面是捕获列表,可以混合捕获
//如果说用到了很多局部对象,也可以不用每个都写进中括号里,可写作[=],自动进行值捕获
//[&] 自动的进行局部对象的引用捕获
//[&, z] 表示使用到的局部对象多是采用引用捕获,z采用值捕获
auto x = [&y, z](int val)
{
++y;
return val >z;
}; //不要忘记这里的分号
std::cout << y << std::endl; //输出的y的值是11.
当去使用不是局部变量的值时,需要使用this进行捕获
struct Str
{
auto fun()
{
int val = 3;
//由于这里的x并不是一个局部的变量,所以要用this,指向Str的一个对象的指针,才能在lambda表达式里使用x
//注意!! this是一个指针,使用过程中可能会有风险,c++17里,使用*this,
//*this就会把Str内的所有内容复制到lambda内部,在调用lambda时更加安全,不会访问已经释放的内存
//但是如果Str比较复杂,复制的时候就会比较耗时间
auto lam = [val, this] ()
{
return val >x;
};
return lam();
}
int x;
};
//写法一:ok
int main()
{
Str s;
s.fun();
}
//写法二:有风险
auto wrapper()
{
Str s;
return s.fun();
}
int main()
{
////如果此时lambda用this,此时wrapper返回的是一个lambda表达式
//this实际是指向wrapper里Str的对象s的一个指针,wrapper调用结束后,s就会被销毁
auto lam = wrapper();
lam(); //指向一个被悬挂的指针,这么调用的行为是未定义的
}
c++14引入了一种新捕获:初始化捕获
std::string a= "hello";
auto lam = [y = std::move(a)]()
{
std::cout << y << std::endl;
};
c++17引入了一种新捕获:初始化捕获
std::string a= "hello";
auto lam = [y = std::move(a)]()
{
std::cout << y << std::endl;
};
接下来来理解说明符:
直接在中括号内用y的话,等效于加了const,如果此时在lambda内改变y的数值是会导致编译报错的
在auto lam这一行后面加上mutable即可解决
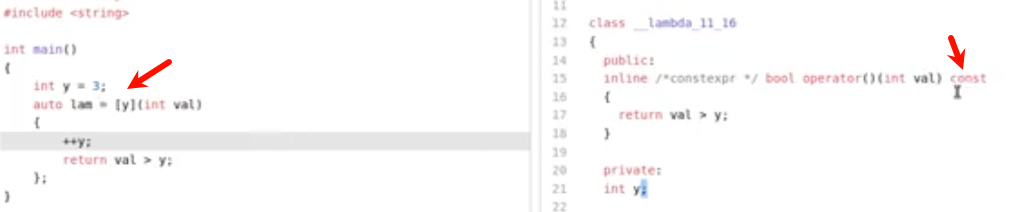
这里使用constexpr(可在运行期or编译器调用)或者consteval(只能在编译期调用),return的值为101
不加的话默认运行期执行。加了的话编译器可以有优化
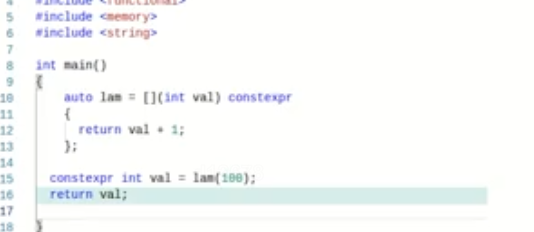
模板形参c++20
任何类型都可以,只要可以支持+1的操作

几种更深入的用法
//c++14捕获时计算,可以一定程度提高效率
int x = 3;
int y = 5;
auto lam = [z = x+y]()
{
return z;
};
//构造完lambda表达式后马上执行 Immediately-invoked function expression
int x = 3;
int y = 5;
auto lam = [z = x+y]()
{
return z;
}();
//比如,这样就可以直接初始化val
const auto val = [z = x+y]()
{
return z;
}();
std::cout<< val << std::endl;
//使用auto避免复制
std::map<int,int> m{{2,3}};
//希望通过这种传引用的方式避免数值,但是实际还是会用到
//改成const std::pair<const int, int>& p才可以不复制,
//c++14时可以直接用auto,改成const auto& p,就可以避免复制
auto lam = [](const std::pair<int, int>& p)
{
return p.first + p.second;
};
std::cout << lam(*m.begin()) << std::endl;
//lifting 用auto实现函数模板
//如果用bind,编译器就不能知道到底要用什么类型
auto fun(int val)
{
return val + 1;
}
auto fun(double val)
{
return val + 1;
}
int main()
{
auto lam = [](auto x)
{
return fun(x);
};
cout << lam(3) << endl;
cout << lam(3.2) << endl;
}
//用lambda表达式实现递归
//报错写法 写阶乘
auto factorial = [](int n){
//这一行会报错. 因为要先把lambda表达式走完,编译器才知道这是lambda表达式
//此时碰到了factorial(n-1),其实不知道这个实际是什么
return n>1? n*factorial(n-1) : 1;
};
cout << factorial(5) << endl;
int factorial(int n) //编译器走完这一行就知道这个是一个函数,所以此递归函数不会报错
{
return n>1 ? n * factorial(n-1) : 1;
}
//如果这么写不会报错。这里用了auto-->模板参数
auto factorial = [](int n)
{
//这里一定要写返回的类型是int,否则内部的return都不知道要返回什么类型f_impl和impl的返回类型成了鸡生蛋问题
auto f_impl = [](int n, const auto& impl) -> int
{
return n>1 ? n * impl(n-1, impl) : 1; //注意这里的impl是一个函数!
};// 内部的lambda表达式声明完毕
return f_impl(n, f_impl); //把f_impl当作了参数!
};
cout << factorial(5) <<endl;
三. 泛型算法的改进——ranges
可以使用容器而非迭代器
std::vector<int> x{1,2,3,4,5};
auto it = std::ranges::find(x,3);
//auto it = std::ranges::find(x.begin(), x.end(),3); //就不用这么写了
std::cout << *it <<std::endl; //output:3
//有问题的写法 dangling悬挂:指向了失效的指针
auto fun()
{
return std::vector<int> x{1,2,3,4,5}; //返回的是一个局部对象,右值,之后会被销毁
}
int main()
{
std::vector<int> x{1,2,3,4,5};
auto it = std::ranges::find(fun(), 3); //使用ranges的时候注意不要传入右值
std::cout << *it <<std::endl; //这种解引用可能是未定义的行为
}
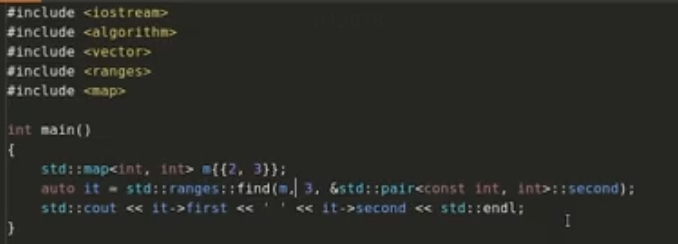
其他的简化代码的写法
 C++泛型算法与bind、lambda表达式详解及ranges应用
C++泛型算法与bind、lambda表达式详解及ranges应用





















 1701
1701

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








