本文深入剖析了一个融合光流和图优化的动态SLAM系统，系统输入包括RGB图像、深度图、像素级实例分割和光流。通过对静态背景的特征追踪和相机位姿估计，结合图优化技术，实现动态物体位姿和轨迹的精确估计。文中详细阐述了位姿表示、3D点坐标转换、物体运动以及相机和物体运动的估计方法，特别强调了光流在稳定追踪和联合估计中的作用。最后，通过局部和全局批量优化，构建并更新局部和全局地图，确保长期追踪的稳定性。该系统在处理遮挡和非直接遮挡情况时表现出良好的鲁棒性，并能实现对物体运动的全局精确化。
一.整体系统
先建立一个感性认识：
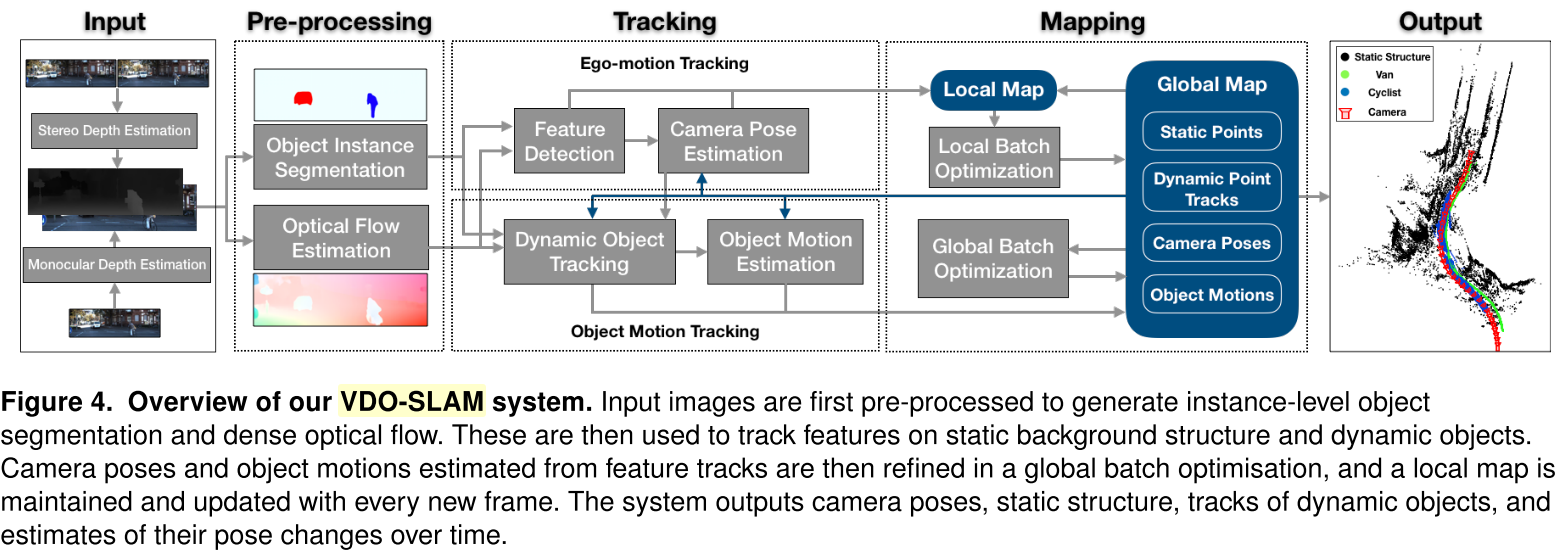系统的输入：双目或单目的rgb图和深度图，像素级实例分割的结果，以及稠密光流。
- 对静态背景进行特征追踪，使用求出的相机pose来求解运动物体pose并对其运动进行估计；
- 用图优化使估计结果更加准确。在这个过程中会维护局部地图，并且随着每一个新帧都会更新。
最终系统的输出是：相机位姿与轨迹，动态物体位姿与轨迹，运动物体的速度，静态地图
二. 几何基础
1. 位姿表示
0Xk∈SE(3)^{0}X_k \in SE(3)0Xk∈SE(3) : 机器人/相机的3D位姿，0为世界坐标系，k是时间戳，也可以理解为是相机坐标系到世界坐标系下的转换矩阵
0Lk∈SE(3)^{0}L_k \in SE(3)0Lk∈SE(3) : 物体的3D位姿，即物体坐标系到世界坐标系下的转换矩阵
2. 3D点的坐标系转换
一个世界坐标系中的第i个3D点(齐次坐标)转换到某一帧k的相机坐标系：
Xkmki=0Xk−1∗ 0mki (1)^{X_k}m^{i}_{k}=^{0}X_k^{-1}* \ ^{0}m_{k}^{i} \ \ \ (1)Xkmki=0Xk−1∗ 0mki (1)
再把这个点从相机坐标系乘以内参矩阵转换到像素坐标系，得到齐次坐标：
Ikpki=π(Xkmki)=K∗ Xkmki (2)^{I_k}p^{i}_k=\pi(^{X_k}m_k^{i})=K* \ ^{X_k}m_k^i \ \ \ (2)Ikpki=π(Xkmki)=K∗ Xkmki (2)
相机和环境中物体的运动都会产生2D光流，可以把从第k-1帧图像到第k帧图像的像素运动写成一个位移向量，这就是光流：
Ikϕi=Ikp~ki−Ik−1pk−1i (3)^{I_k}\phi^i = ^{I_k}\widetilde{p}_k^i - ^{I_{k-1}}p_{k-1}^i\ \ \ (3)Ikϕi=Ikpki−Ik−1pk−1i (3)
相当于说，我们可以得到第k-1帧第i点的像素坐标，然后可以通过光流法找到第k帧中对应的像素点(带波浪线的项)。这篇论文就是使用光流法对相邻帧进行追踪。
3. 物体和3D点的运动
物体在相邻帧之间的位姿变换，可以用下式表示：
k−1Lk−1Hk=0Lk−1−1∗ 0Lk (4)^{L_{k-1}}_{k-1}H_k= ^{0}L_{k-1}^{-1} * \ ^{0}L_k \ \ \ (4)k−1Lk−1Hk=0Lk−1−1∗ 0Lk (4)
个人理解：0Lk^{0}L_k0Lk是第k帧时物体坐标系到世界坐标系下的转换矩阵；而0Lk−1−1^{0}L_{k-1}^{-1}0Lk−1−1是第k-1帧时世界坐标系到物体坐标系的变换矩阵。所以求出的就是从第k帧到第k-1帧物体位姿的变换矩阵
在这个物体(刚体)上的点坐标系变换就如下，表示第k帧时这个点从世界坐标系转到这个物体坐标系的位置：
Lkmki=0Lk−1∗ 0mki (5)^{L_k}m_k^i = ^0L_k^{-1} * \ ^0m_k^i \ \ \ (5)Lkmki=0Lk−1∗ 0mki (5)
那么，此时我们就可以得到物体上某一点在世界坐标系的位置和该点在这个物体坐标系位置的坐标转换关系(把式4代入式5)：
0mki=0Lk∗Lkmki=0Lk−1∗k−1Lk−1Hk∗Lkmki (6)^0m^i_k = ^0L_k * ^{L_k}m_k^i = ^0L_{k-1} * ^{L_{k-1}}_{k-1}H_k* ^{L_k} m_k^i \ \ \ (6)0mki=0Lk∗Lkmki=0Lk−1∗k−1Lk−1Hk∗Lkmki (6)
注意：对于刚体来说，刚体上的某一点相对这个刚体坐标系(以刚体上某一点作为坐标系原点)是固定的，也就是说Lkmki^{L_k}m_k^iLkmki在物体坐标系的坐标为定值Lmi^Lm^iLmi,不管时间戳是多少，都不会变。所以说式6的最后一项为：（这里的n可以是任何整数）
Lkmki=Lmi=0Lk−1∗0mki=0Lk+n−1∗0mk+ni (7)^{L_k}m_k^i =^Lm^i=^0L_k^{-1}*^0m_k^i=^{0}L_{k+n}^{-1} *^0m_{k+n}^i \ \ (7) Lkmki=Lmi=0Lk−1∗0mki=0Lk+n−1∗0mk+ni (7)
为了表示当前帧和上一帧之间的关系，将式7中的n设置为-1，然后代入式6得到式8，这个式子非常重要：
0mki=0Lk−1∗k−1Lk−1Hk∗0Lk−1−1∗0mk−1i (8)^0m^i_k = ^0L_{k-1} * ^{L_{k-1}}_{k-1}H_k* ^{0}L_{k-1}^{-1} *^0m_{k-1}^i \ \ \ (8)0mki=0Lk−1∗k−1Lk−1Hk∗0Lk−1−1∗0mk−1i (8)
这里稍微暂停一下来理解这个式子，其实很好理解，从右向左，把一个第k-1帧在世界坐标系下的3D点，先把它转到第k-1帧所在物体的坐标系，因为是刚体，所以这个点在第k-1帧的物体坐标系和第k帧的物体坐标系下时，坐标值是一样的，所以最右边两项等价于，第k帧的3D点在第k帧物体坐标系下的位置；0Lk−1∗k−1Lk−1Hk^0L_{k-1} * ^{L_{k-1}}_{k-1}H_k0Lk−1∗k−1Lk−1Hk表示的是第k帧物体坐标系到世界坐标系的转换矩阵。所以整个式子就相当于是把第k帧的3D点从第k帧的物体坐标系转到了世界坐标系。
除此之外，式8还有一种理解方式，就是令k−10Hk:=0Lk−1∗k−1Lk−1Hk∗0Lk−1−1^0_{k-1}H_k:=^0L_{k-1} * ^{L_{k-1}}_{k-1}H_k* ^{0}L_{k-1}^{-1}k−10Hk:=0Lk−1∗k−1Lk−1Hk∗0Lk−1−1看成一个整体，相当于我们可以得到世界坐标系下，刚体上同一点在相邻帧间位置的变换关系:
0mki=k−10Hk∗0mk−1i, k−10Hk∈SE(3) (9)^0m^i_k = ^0_{k-1}H_k * ^0m_{k-1}^i , \ \ \ ^0_{k-1}H_k \in SE(3)\ \ \ \ (9)0mki=k−10Hk∗0mk−1i, k−10Hk∈SE(3) (9)
公式9是这篇论文进行运动估计的核心。它以无模型的方式用位于物体上的点来表达刚体的位姿变化，而不需要将物体的三维位姿作为随机变量纳入估计中。这个矩阵k−10Hk^0_{k-1}H_kk−10Hk之后被称为‘object pose change’或者是‘object motion’。
三. 相机位姿和物体运动估计
1. 相机位姿估计
这一步和常规的SLAM类似，已知环境中第k-1帧静态3D地图点的世界坐标，和图像中的2D匹配点对，相机位姿0Xk^0X_k0Xk可以通过最小化重投影误差求出：
ei(0Xk)=Ikp~ki−π(0Xk−1∗0mk−1i) (10)e_i(^0X_k)=^{I_k}\widetilde{p}_k^i - \pi(^0X_k^{-1} * ^0m_{k-1}^i) \ \ \ (10)ei(0Xk)=Ikpki−π(0Xk−1∗0mk−1i) (10)
在论文中，作者使用李代数xk∈se(3)x_k \in se(3)xk∈se(3)来对SE(3)的相机位姿进行参数化：
0Xk=exp(0xk) (11)^0X_k = exp(^0x_k) \ \ \ (11)0Xk=exp(0xk) (11)
而0xk∨^0x_k^{\vee}0xk∨表示从se(3)到R6\mathbb{R}^6R6的映射。这时，把式11代入式10，就可以得到最小二乘的代价公式如下，相机位姿是通过LM算法来求解的：
0xk∗∨=arg min0xk∨∑inbρh(eiT(0xk)Σp−1ei(0xk)) (12)^0x_k^{*\vee}=\argmin_{^0x_k^{\vee}} \sum^{n_b}_i \rho_h (e_i^T(^0x_k)\Sigma^{-1}_p e_i(^0x_k)) \ \ \ (12)0xk∗∨=0xk∨argmini∑nbρh(eiT(0xk)Σp−1ei(0xk)) (12)
这个公式中，nbn_bnb是相邻帧之间3D-2D静态匹配点对的个数，ρh\rho_hρh是Huber核函数，Σp\Sigma_pΣp是协方差矩阵。
2. 物体运动估计
要求物体的运动，也就是求k−10Hk^0_{k-1}H_kk−10Hk，根据公式9，可以写出某物体上3D点和它对应2D点的重投影误差：
ei(k−10Hk):=Ikp~ki−π(0Xk−1∗k−10Hk∗0mk−1i)=Ikp~ki−π(k−10Gk∗0mk−1i) (13)e_i(^0_{k-1}H_k):=^{I_k}\widetilde{p}_k^i - \pi(^0X_k^{-1} * _{k-1}^0H_k * ^0m_{k-1}^i) \\ =^{I_k}\widetilde{p}_k^i - \pi(^0_{k-1}G_k * ^0m_{k-1}^i) \ \ \ (13)ei(k−10Hk):=Ikpki−π(0Xk−1∗k−10Hk∗0mk−1i)=Ikpki−π(k−10Gk∗0mk−1i) (13)
这里的k−10Gk∈SE(3)^0_{k-1}G_k \in SE(3)k−10Gk∈SE(3)，参数化k−10Gk∈SE(3):=exp(k−10gk), k−10gk∈se(3)^0_{k-1}G_k \in SE(3):=exp(^0_{k-1}g_k), \ \ ^0_{k-1}g_k \in se(3)k−10Gk∈SE(3):=exp(k−10gk), k−10gk∈se(3)， 通过最小化下面的误差可以找到优化的解：
k−10gk∗∨=arg mink−10gk∨∑indρh(eiT(k−10gk)Σp−1ei(k−10gk)) (14) ^0_{k-1}g_k^{*\vee}=\argmin_{^0_{k-1}g_k^{\vee}} \sum_i^{n_d}\rho_h(e_i^T(^0_{k-1}g_k)\Sigma_p^{-1}e_i(^0_{k-1}g_k)) \ \ \ (14)k−10gk∗∨=k−10gk∨argmini∑ndρh(eiT(k−10gk)Σp−1ei(k−10gk)) (14)
这里的ndn_dnd是从第k-1帧到第k帧所有3D-2D的动态点匹配对。把待优化项求出来并映射回SE(3)之后，就可以求k−10Hk=0Xk∗k−10Gk^0_{k-1}H_k=^0X_k * _{k-1}^0G_kk−10Hk=0Xk∗k−10Gk
3. 和光流的联合估计
相机位姿和物体运动估计都依赖于好的图像匹配对。由于遮挡，大的相对运动，大的相机-物体距离，对运动物体上的点进行追踪是很难的。为了能够稳定的追踪点，这篇论文会联合光流估计和运动估计。
光流+相机位姿估计
在原来的公式10中加入光流：
ei(0Xk)=Ikp~ki−π(0Xk−1∗0mk−1i) (10)e_i(^0X_k)=^{I_k}\widetilde{p}_k^i - \pi(^0X_k^{-1} * ^0m_{k-1}^i) \ \ \ (10)ei(0Xk)=Ikpki−π(0Xk−1∗0mk−1i) (10)
ei(0Xk,Ikϕ)=Ik−1pk−1i+Ikϕi−π(0Xk−1∗0mk−1i) (15)e_i(^0X_k, ^{I_k}\phi)=^{I_k-1}p_{k-1}^i + ^{I_k}\phi^i - \pi(^0X_k^{-1} * ^0m_{k-1}^i) \ \ \ (15)ei(0Xk,Ikϕ)=Ik−1pk−1i+Ikϕi−π(0Xk−1∗0mk−1i) (15)
变成李代数的形式就如下：
{0xk∗∨, kΦk∗}=arg min0xk∨,kΦk∑inb{ρh(eiT(Ikϕi)Σϕ−1ei(Ikϕi))+ρh(eiT(0xk,Ikϕi)Σp−1ei(0xk,Ikϕi))} (16)\{^0x_k^{*\vee}, \ ^k\Phi_k^*\}=\argmin_{^0x_k^{\vee}, ^k\Phi_k} \sum^{n_b}_i \{\rho_h (e_i^T(^{I_k}\phi^i)\Sigma^{-1}_{\phi} e_i(^{I_k}\phi^i)) + \rho_h (e_i^T(^0x_k, ^{I_k}\phi^i)\Sigma^{-1}_p e_i(^0x_k, ^{I_k}\phi^i))\} \ \ \ (16){0xk∗∨, kΦk∗}=0xk∨,kΦkargmini∑nb{ρh(eiT(Ikϕi)Σϕ−1ei(Ikϕi))+ρh(eiT(0xk,Ikϕi)Σp−1ei(0xk,Ikϕi))} (16)
其中，ei(Ikϕi)=Ikϕ^i−Ikϕie_i(^{I_k}\phi^i)=^{I_k}\hat{\phi}^i - ^{I_k}\phi^iei(Ikϕi)=Ikϕ^i−Ikϕi，第一项是通过传统或学习的方法获得的初始光流。
光流+物体运动估计
{k−10gk∗∨, kΦk∗}=arg mink−10gk∨,kΦk∑inb{ρh(eiT(Ikϕi)Σϕ−1ei(Ikϕi))+ρh(eiT(k−10gk,Ikϕi)Σp−1ei(k−10gk,Ikϕi))} (16)\{^0_{k-1}g_k^{*\vee}, \ ^k\Phi_k^*\}=\argmin_{^0_{k-1}g_k^{\vee}, ^k\Phi_k} \sum^{n_b}_i \{\rho_h (e_i^T(^{I_k}\phi^i)\Sigma^{-1}_{\phi} e_i(^{I_k}\phi^i)) + \rho_h (e_i^T(^0_{k-1}g_k, ^{I_k}\phi^i)\Sigma^{-1}_p e_i(^0_{k-1}g_k, ^{I_k}\phi^i))\} \ \ \ (16){k−10gk∗∨, kΦk∗}=k−10gk∨,kΦkargmini∑nb{ρh(eiT(Ikϕi)Σϕ−1ei(Ikϕi))+ρh(eiT(k−10gk,Ikϕi)Σp−1ei(k−10gk,Ikϕi))} (16)
四. 图优化
为了精确相机位姿和物体运动，建立起一个全局一致的包括静态和动态结构的图，论文把这个动态slam的问题构建成了一个图优化问题。
黑色方块代表不同时间戳的相机位姿，蓝色方块代表3个静态点，红色方块代表不同时刻某物体(虚线框)上相同的动态点，绿色方块表示物体位姿在帧间的变换。在这个示意图中，只标出了动态物体上的一个红方块，但实际上会使用所有在动态物体上的点。黑色圆圈表示先验的的一元因子，橙色与安全标示里程计的二元因子，白色圆圈是点测量的二元因子，枚红圈是点运动的三元因子，青色圈是一个光滑运动二元因子。
这个图中有4种观测值，也就对应四种误差项(边)：
3D点的测量值： 这种观测模型的误差为ei,k(0Xk,0mki)=0Xk−1∗0mki−zkie_{i,k}(^0X_k, ^0m_k^i) = ^0X_k^{-1} * ^0m_k^i - z^i_kei,k(0Xk,0mki)=0Xk−1∗0mki−zki, 3D观测因子就是图中的白圈，是个二元因子。
视觉里程计的测量值： 这里把Tracking模块中的相机位姿估计视为了一个测量值，论文中说是因为这个由3D-2D误差最小化出来的结果质量比较好。这个视觉里程计模型误差项为ek(0Xk−1,0Xk)=(0Xk−1−1∗0Xk)−1−k−1Xk−1Tke_k(^0X_{k-1}, ^0X_k) = (^0X_{k-1}^{-1} *^0X_k )^{-1} - ^{X_{k-1}}_{k-1}T_kek(0Xk−1,0Xk)=(0Xk−1−1∗0Xk)−1−k−1Xk−1Tk. 里程计因子是图中的橙色圈。
动态物体上点的运动观测(上面的H矩阵)： 动态物体上点的运动误差为
ei,j,k(0mki,k−10Hkl,0mk−1i)=0mki−k−10Hkl∗0mk−1ie_{i,j,k}(^{0}m_k^i, _{k-1}^0H_k^l, ^0m_{k-1}^i)=^0m_k^i-_{k-1}^0H^l_k*^0m_{k-1}^iei,j,k(0mki,k−10Hkl,0mk−1i)=0mki−k−10Hkl∗0mk−1i，对应于上面枚红色的圆圈，是一个三元因子。对于一个刚体上的点，他们的位姿变换理论上是一样的。
物体平滑运动的观测： 根据物理世界中相对大的物体不会发生运动突变的规律，所以这里加入了平滑运动因子来最小化相邻帧间物体运动的变化。误差项被定义为：el.k(k−20Hk−1l,k−10Hkl)=(k−20Hk−1l)−1∗k−10Hkle_{l.k}(^0_{k-2}H_{k-1}^l, ^0_{k-1}H_k^l)=(^0_{k-2}H^l_{k-1})^{-1} * ^0_{k-1}H^l_kel.k(k−20Hk−1l,k−10Hkl)=(k−20Hk−1l)−1∗k−10Hkl. 这一个误差因子对应于图中青色圆圈。
而图中的所有节点，是由所有的3D点，所有的相机位姿，还有所有的object motion(就是前面提到的世界坐标系下，动态物体上的同一点在相邻帧的变换)。最终是用李代数进行参数化，用LM求解。
最小二乘的代价函数是：
五. 系统细节
这个系统有两个难点：
- 稳定的分割出静态背景和物体：使用了语义分割和实例分割的结果
- 保证动态物体的长期追踪： 使用了稠密光流，来最大化移动物体上的追踪点个数。因为如果只用稀疏特征点匹配，无法保证对一些小的移动物体的追踪。同时，还可以用稠密光流来连续跟踪多个物体（通过传播一个唯一的物体标识符，这个标识符会被分配给物体mask上每一个点）；在语义分割失效时，稠密光流还可以恢复物体的mask。
1. 追踪模块
a. 静态特征点和相机位姿估计
静态特征点是在去除了物体mask的区域进行提取的，来保证这些角点在静态背景。相机位姿是通过使用公式15和3D-2D匹配点对来求解的。在求解之前，会对位姿有一个初始估计，这里估计用到了两种方法：1)匀速运动模型；2)带有RANSAC的P3P算法。哪种方法生成的内点更多就用哪种方式初始化。
b. 动态物体追踪
这里起始分为了两步：
- 把分割出来的物体划分为静态或者动态(为了减少运算量)
- 在连续帧之间关联动态物体
第一步使用了场景流估计的方法来识别动态物体。光流是点在2D平面内的运动，而场景流是点在3D空间里的运动。在已知相机位姿0Xk^0X_k0Xk之后，就可以求出3D点在第k-1帧和第k帧的运动，即场景流向量：
fki=0mk−1i−0mki=0mk−1i−0Xk∗Xkmkif^i_k=^0m_{k-1}^i-^0m_k^i=^0m_{k-1}^i-^0X_k * ^{X_k}m_k^ifki=0mk−1i−0mki=0mk−1i−0Xk∗Xkmki
和光流不同，场景流在理想情况下只受场景中物体运动的影响（理解是坐标系是直接在世界坐标系下的）。理想情况下，静态点的场景流求出来就是0，但是因为一些深度值和匹配的误差，这个结果往往不会是0。论文中对每个物体的所有采样点都计算了场景流，如果其中某一个的场景流的量大于阈值0.12，那么这个点就被视为动态点；如果一个物体中有超过30%的点是动态点，那么这个物体就是动态物体，否则仍然为静态物体（但是前面求相机位姿的时候并没有用到静态物体，不知道后面会不会使用？）。然后，作者在这里提到也考虑过把阈值设为0的情况，这样所有物体先一律视为动态，如果是静态的话，后续求出来按理应该速度为0，但作者说这样设置反而降低了系统的表现。
实例分割可以对每一帧进行物体的标记，即给每个像素都加上一个标签，但是做到这里还没有实现帧和帧之间的跟踪。这里作者是用光流法来追踪每个点在跨帧的Label。对于静态物体和背景，标签为0，其他动态物体，每检测到一个新的，标签数字就加一。理想情况下：一个在第k帧被检测到的物体，它上面所有点的label都应该是和它上一帧的对应点唯一关联的，但现实是只能把第k帧所有点和它对应点上出现最多的label对应起来。比如说：第k帧是动态的物体，如果上一帧中它最常见的label是0，就说明是这个物体开始移动了，或者是这个物体在边界处出现，或者是在受到遮挡后又出现了，这种情况下，这个物体要被赋予新的追踪标签。
c. 物体运动估计
在物体的mask内，每3个点采样一次，然后在帧间跟踪他们。和相机位姿估计类似，只有内点才会被存进地图，用于追踪下一帧，当追踪的物体点数量降低到阈值之下，就会采样新的物体点。对于物体的初始运动模型，和a小节中类似。
2. 建图
这里说到了一个局部地图和全局地图
a. 局部批量优化
这里的局部地图是取的前nw=20n_w=20nw=20帧的地图，有4帧重叠。作者在这里说只局部优化相机位姿和滑窗中的静态结构，因为局部优化动态结构对整个优化问题没有好处，除非加入一个匀速运动物体的强约束。作者在这里说局部优化这里可以优化动态和静态结构，但是并没有选择这么做。当局部地图构建出来后，就会进行因子图优化来使局部地图中的变量求解更加精确，然后再把这些值更新到全局地图中。
b. 全局批量优化
追踪模块和局部批量优化模块的输出包括相机位姿、物体运动和内点结构。这些都被保存在一个全局图中，该图是由以前所有的时间步构建的，并随着每一个新的帧不断地被更新。在处理完所有的输入帧后，就会基于全局地图构建一个因子图。为了有效地探索时间约束，只有那些被跟踪超过3个实例的点才会被添加到因子图中。因子图优化的结果作为整个系统的输出。
c. 从建图到追踪
这一节我觉得作者是想说明建图和追踪模块之间的联系。
通过地图的历史信息可以来估计当前帧的状态，上图中的蓝色箭头就是这一过程的示意。上一帧中的内点可以用来和当前帧进行匹配，从而估计出当前帧相机位姿和物体运动。上一帧相机和物体运动也可以被用作先验模型，可能会被用来作为当前估计的初始值。物体上的点还能用来关联帧之间的语义mask，来实现稳定的追踪，具体方法是：在语义物体分割失败导致的 "间接遮挡 "的情况下，传播其先前分割的掩模。
六. 结果讨论
这里作者定义了旋转，平移的误差项，还有速度的计算方法，和其他方法的外部比较这里先不贴上来，对照论文即可，想记录的是几个Discussion里面的点，这里主要是讨论了作者这么设计这个系统的一些好处：
-
联合光流的优化使得更多的点能被连续追踪，这就使得通过这些点求出来值的精度能有小幅提升(15%~20%)。
-
增强了对非直接遮挡情况的鲁棒性：对于语义分割，他可能会在发生直接遮挡以及非直接遮挡(光照变化)时失效, 在非直接遮挡的情况下，把之前的语义mask传播到当前帧可以解决这个问题。下面用图来举一个具体例子：
序列一共有88帧，要追踪其中的白色车子，从第33帧开始，语义分割失效，但是追踪仍然可以进行。可以看到序列的后半段平均误差较大，这是因为此时有局部的直接遮挡（有车子局部是看不到的），以及物体离相机太远。
右下角白车上的点是把之前追踪的特征点传播到了当前帧
-
对物体运动的全局精确化：从下面的图可以看出来，速度估计是不平滑的，而且在后半段有很大的误差，这主要是因为物体距离相机越来越远，只在整个场景中占据了一小部分。这时，如果只靠传感器的测量值来做运动估计是很困难的，所以就使用了前面的因子图优化，可以看到结果更加平滑且提升明显。
-
实时性：帧率在5-8帧，会受到场景中移动物体的数目的影响。全局优化的耗时受相机帧总数，每帧移动物体数目的影响
扫一扫
8469
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
