CodeForces - Antenna Coverage（区间DP）

最新推荐文章于 2022-08-16 21:52:06 发布

原创最新推荐文章于 2022-08-16 21:52:06 发布 · 568 阅读

4 ·

CC 4.0 BY-SA版权

Algorithm、数据结构专栏收录该内容

65 篇文章

订阅专栏

这篇博客探讨了一个线段覆盖问题，其中涉及到n个路灯在一条长度为m的线段上，每个路灯有自己的照明范围。问题目标是最小化扩展路灯照明范围以覆盖整个线段所需的硬币花费。博主通过动态规划的方法，使用dp[i]表示线段[1,i]被覆盖的最小代价，并详细阐述了状态转移方程。最后，提供了AC代码实现该算法，时间复杂度为O(n*m)。

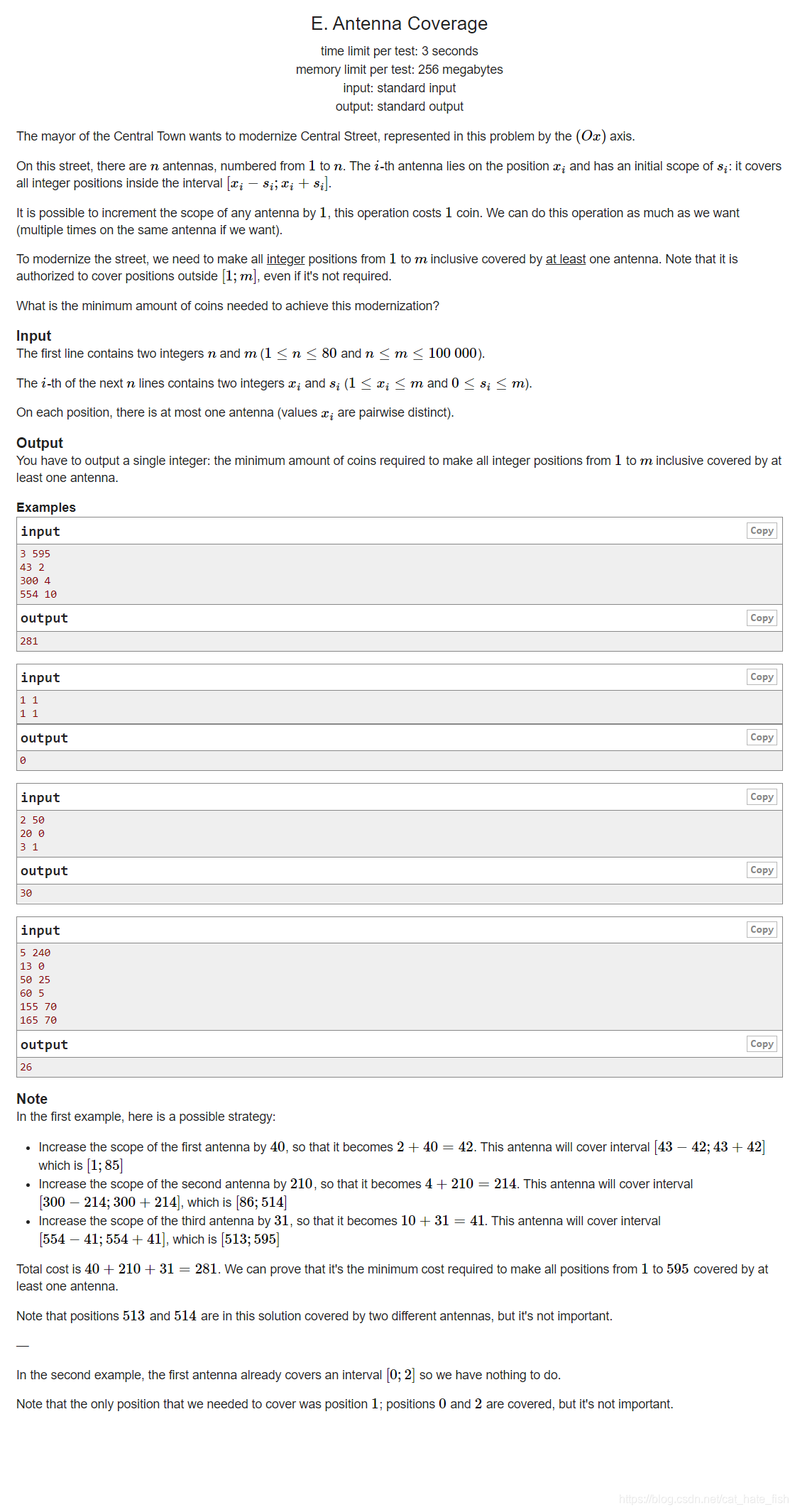
在这里插入图片描述

题意：

给一段长度为m的线段，线段上有n个路灯，
每个路灯在位置 $x_i$ 且能照亮范围 $x_i-s_i,x_i+s_i]$
我们可以花费一个硬币使得某个路灯的 $s_i$ 的增大1，可以操作任意多次
求能使区间[1,m]被路灯照亮的最小硬币花费

思路：

dp[i]表示线段 $[1, i]$ 被覆盖所需的最小代价

第一层循环dp从1到m，第二层循环遍历n个路灯，维护dp
时间复杂度O(n*m)

状态转移分析：

$x [j] < = i$ :路灯在当前位置的左边的时候
1. $x [j] + s [j] > = i$ :第 $j$ 个路灯可以照亮位置 $i$
  $d p [i] = m i n (d p [i], d p [m a x (0 ， x [j] - s [j] - 1)])$
2. $x [j] + s [j] < i$ :第 $j$ 个路灯照不到位置 $i$ ，需要扩展 $s [j]$
  $d p [i] = m i n (d p [i], d p [m a x (0 ， 2 * x [j] - i - 1)] + (i - x [j] - s [j]))$
$x [j] > i$ :路灯在当前位置的右边的时候
1. $x [j] - s [j] < = i$ :第 $j$ 个路灯可以照亮位置 $i$
  $d p [i] = m i n (d p [i] ， d p [m a x (0 ， x [j] - s [j] - 1)])$
2. $x [j] - s [j] > i$ :第 $j$ 个路灯不能照亮位置 $i$
  不用扩展

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,x[maxn],s[maxn],dp[maxn];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>x[i]>>s[i];
	for(int i=1;i<=m;i++) dp[i]=i;
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			if(x[j]<=i)
				dp[i]=min(dp[i],dp[max(0,min(2*x[j]-i-1,x[j]-s[j]-1))]+max(0,i-(x[j]+s[j])));
			else
				dp[i]=min(dp[i],dp[max(0,x[j]-s[j]-1)]);
		}
	}
	cout<<dp[m]<<endl; 
}