【恍然一悟】用递归过程思考 [辗转相除法|欧几里得算法] 原理，附代码（leetCode1979 找出数组的最大公约数）

原创已于 2024-09-22 14:23:42 修改 · 1k 阅读

31 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2024-09-22 01:43:07 首次发布

算法与数据结构专栏收录该内容

4 篇文章

订阅专栏

文章目录

❀ 前情[一点业务无关的前因后果碎碎念]

通勤时间长，一直断断续续利用这个时间阅读。

最近点开了一本非常简单不费脑的概念科普读物《我的第一本算法书》，看到第7章“欧几里得算法”时还在想这是什么，长知识了长知识了，来，让我们揭开这个知识的神秘面纱~
在这里插入图片描述
一看，嚯，老伙计原来是你~

那年杏花微雨……我听说你的名字叫辗转相除法（欧几里得算法名称源于：该算法最早被发现记载于公元前300年欧几里得的著作中；辗转相除法则是更加见名知意的叫法）

在还只会C语言、在学for循环的大一年纪，曾在课后练习中被这个优雅解法深深震撼。作为一只不太见多识广的九漏鱼，对于公约数求解我只见过小学那种解法，belike ↓：
在这里插入图片描述
惊艳，深深的惊艳，然后小小的眼睛就有了大大的疑问？

为什么呢？这个辗转相除法为什么能发挥作用呢？

彼时我像画二叉树一样把数字分解，似懂非懂地明白了。

回想起当时画的图，发现当时的思考就是在模拟递归的过程，今久别重逢，便想试着用递归处理下它。当然，从编码角度来说，一般情况下，循环和递归本就是能互转的。

一、探索辗转相除法原理

1. 辗转相除法计算步骤

求a和b的最大公约数（a > b）
用辗转相除法来做，粗暴点说就一句话： 余数c = a%b，此后一直用除数对余数取余，直到结果为0

2.书中内容摘选

《我的第一本算法书》以1112和695为例，计算了这个过程。
在这里插入图片描述
也做了相应的图解

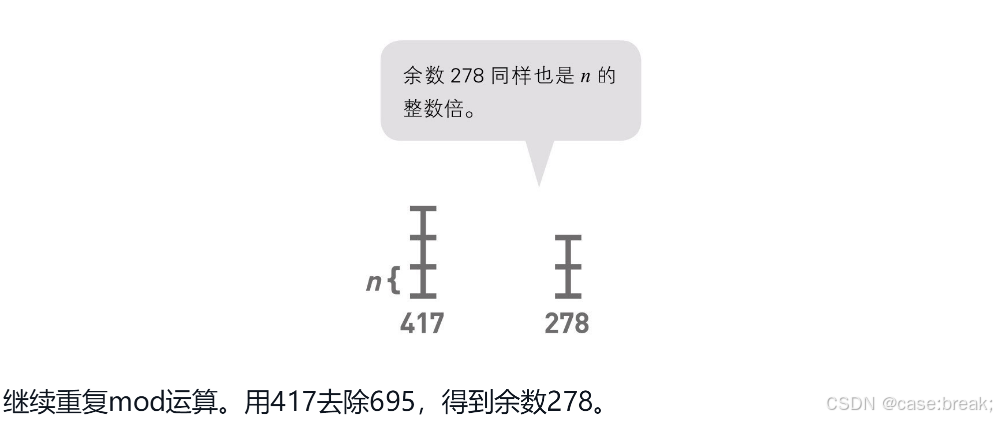
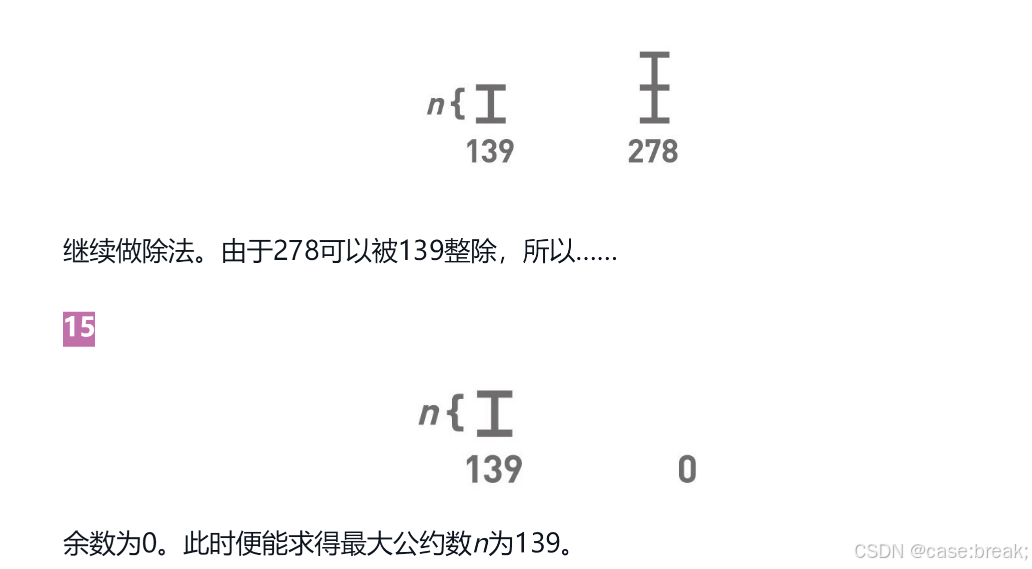
整个取余的过程有点像强迫症削甘蔗，要把两根不同长度的甘蔗均分。于是互相适配，拿互不相同的部分（余数）试探长度，直至达成同一长度。

2.画图递归理解

其实通过用类似树的图形去分解数据，看起来更为直观。

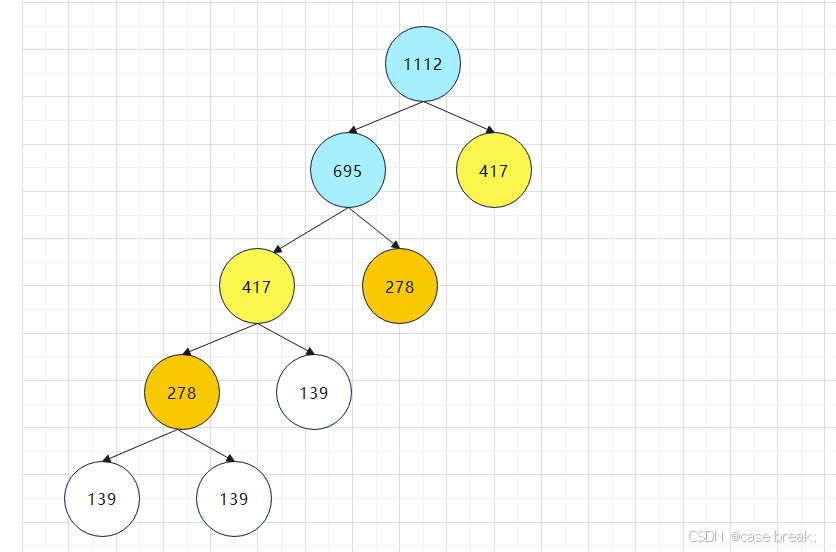
在这里插入图片描述

整个计算过程的数据拆分如图所示，蓝色部分为初始数据。除根节点外，每层节点左边是除数，右边是余数，每层数值加起来等于父节点的值，每层的余数是下一层的除数。

从上往下计算到终点后，从这个图就很直观地能观察出，每个节点都能由叶子节点构成。1112和695的例子凑巧整除结果为1，但即使是多倍，也无非同一层中多几个和除数的值相同的节点而已。

3.公式推导

网上可以搜出很多比较规范的证明过程，百科也有
https://baike.baidu.com/item/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E7%AE%97%E6%B3%95/1647675

所以在此我就不班门弄斧，只简单沿着递归的思路往下推算。
若 a % b = R1
则 a = n1 * b + R1
假设 b % R1= R2
则 b = n2* R1 + R2
…… 一直往下算可以发现都是由余数R1、R2 … Rn 在表达这些数值关系，所以当Rn 与 Rn-1 存在倍数关系后，Rn就可以通过倍数关系表达初始数据a和b。

二、代码解题：LeetCode1979 找出数组的最大公约数

给你一个整数数组 nums ，返回数组中最大数和最小数的最大公约数。
两个数的最大公约数是能够被两个数整除的最大正整数。

class Solution {
    public int findGCD(int[] nums) {
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
        for(int i = 0 ; i < nums.length; i++){
            if(nums[i] > max){
                max = nums[i];
            }
            if(nums[i] < min){
                min = nums[i];
            }
        }
        return realFindGCD(max, min);
    }
	//通过递归计算a、b的最大公约数
    public int realFindGCD(int a, int b){
        if(a % b == 0){
            return b;
        }
        return realFindGCD(b, a%b);
    }
}