Summer 1_summer canvas-优快云博客

博客主要包含三部分内容，一是给出程序1和程序2的运行结果；二是指出宏定义的宏展开在预处理阶段完成；三是给出一道算法题，即在特定二维数组中判断是否含某整数，介绍了定位法求解，时间复杂度为O(row+col)。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.下面程序的运行结果

// 1.
int main()
{
	int a[] = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 };
	int *q[4];
	int k;

	for (k = 0; k < 4; k++)
	{
		q[k] = &a[k * 3];
	}
	printf("%d\n", q[3][1]);
	system("pause");
	return 0;
}

//2
int main()
{
	int i, j, a = 0;
	for (i = 0; i < 2; i++)
	{
		for (j = 0; j < 4; j++)
		{
			if (j % 2)
				break;
			a++;
		}
		a++;
	}
	printf("%d\n", a);

	const char *p = "Hello!";
	printf("%c\n", *p);
	system("pause");
	return 0;
}

程序1的结果为22. 程序2的结果是4, H

2.宏定义的宏展开是在预处理阶段完成的

3.算法题

在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序. 请完成一个函数,输入这样的一个二维数组和一个整数,并判断数组中是否含有该整数. 时间复杂度 O(row+col)

数组样例
int arr[4][4]={
1,2,8,9
2,4,9,12
4,7,10,13
6,8,11,15};

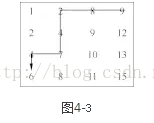
解法：定位法

如图 4-3所示，首先直接定位到矩阵中最右上角的元素，如果这个元素比要找的数6大就往左走，比要找的数6小就往下走，直到找到要找的数6为止。这个方法的时间复杂度是O(row+col)。

#define ROW 4
#define COL 4
 
bool YoungMatrix(int array[][COL], int searchKey)
{
     int i = 0, j = COL - 1;
     int var = array[i][j];
     while (true)
     {
         if (var == searchKey)
         {
             return true;
         }
         else if (var < searchKey && i < ROW - 1)
         {
             var = array[++i][j];
         }
         else if (var > searchKey && j > 0)
         {
             var = array[i][--j];
         }
         else
         {
             return false;
         }
     }
}