有序序列L1和L2的中位数问题

一 概述

一个长度为L（L>=1）的升序序列S，处在第[L/2]个位置的数称为S的中位数。

• 即：S1 = (11,13,15,17,19)的中位数为15；
• S2 = (11,13,15,17)的中位数为13； 

当然求中位数时应该注意以下几个细节问题： 

前提：分别求两个有序序列L1，L2的中位数mid1，mid2; 

1.如果mid1=mid2,则mid1或者mid2极为有序序列L1和L2的中位数。

2.若mid1<mid2,则舍弃序列L1中间点以前的部分,同时舍弃序列L2中间点以后的部分

• 当L1序列长为奇数: 舍弃L1中间点以前的部分且保留中间点。
• 当L1序列长为偶数：舍弃L1中间点以前的部分不保留中间点。 

3.若mid1>mid2,则舍弃序列L1中间点以后的部分，同时舍弃序列L2中间点前的部分

• 当L1序列长为奇数：舍弃L1中间点以后的部分且保留中间点。
• 当L1序列长为偶数：舍弃L1中间点以后部分且保留中间点。

序列L2同理，序列长奇偶性类同。 

二 代码实现

#include <iostream>
using namespace std;
typedef int ElemType; 
#define MAXSIZE 100
#define ERROR 0
#define OK 1

typedef struct {
	
	ElemType *elem;
	int length;
}SqList;

int InitOrderList(SqList &L1,SqList &L2){
	
	L1.elem = new ElemType[MAXSIZE];
	L2.elem = new ElemType[MAXSIZE];
	
	if(!L1.elem || !L2.elem){
		
		return ERROR;
	}
	
	return OK;
}

ElemType GetMidValue(SqList L1,SqList L2){
	
	int low1 = 0, high1 = L1.length-1, mid1;
	int low2 = 0, high2 = L2.length-1, mid2;
	
	while(low1  != high1 || low2 != high2){
		
		mid1 = (low1 + high1) / 2;
		mid2 = (low2 + high2) / 2;
		
		if(L1.elem[mid1] == L2.elem[mid2]) {
			return L1.elem[mid1];
		}
		
		if(L1.elem[mid1] < L2.elem[mid2]) {
			if((low1+high1)%2==0){  //当序列中数据个数为奇数 
				low1 = mid1;	    //删除序列L1中间值前的部分且保留中间值 
				high2 = mid2;		//删除序列L2中间值后的部分且保留中间值 
			}else{				  	//当表中数据个数为偶数 
				low1 = mid1 + 1;  	//删除序列L1中间值前的部分且不保留中间值 
				high2 =  mid2;		//删除序列L2中间值后的部分且保留中间值 
			}
		}else{
			if((low2+high2)%2==0){  //当序列中数据个数为奇数 
				high1 = mid1;	    //删除序列L1中间值前的部分且保留中间值 
				low2 = mid2;		//删除序列L2中间值后的部分且保留中间值 
			}else{					//当表中数据个数为偶数 
				high1 = mid1;  		//删除序列L1中间值后的部分且保留中间值 
				low2 = mid2 + 1;	//删除序列L2中间值前的部分且不保留中间值 
			}
		} 
	}
	
	return L1.elem[low1] < L2.elem[low2] ? L1.elem[low1] : L2.elem[low2];
}

int main(){
	
	SqList L1,L2;
	int select = -1,i;
	int n;
	
	cout<<"寻找有序表L1和L2的中值!"<<endl;
	cout<<"1.初始化有序线性表!"<<endl;
	cout<<"2.插入n个数到有序表L1!"<<endl;
	cout<<"3.插入n个数到有序表L2!"<<endl;
	cout<<"4.有序表L1和L2的中值midValue!"<<endl;
	cout<<"0.退出!"<<endl;
	
	while(select != 0){
		
		cout<<"请选择：";
		cin>>select; 
		switch(select){
			case 1:
				if(InitOrderList(L1,L2)){
					cout<<"有序表初始化成功！"<<endl ; 
				}else{
					cout<<"有序表初始化失败！"<<endl;
				} 
				break;
			case 2:
				cout<<"输入序列L1的长度：";
				cin>>n;
				cout<<"输入序列L1：";
				for(i = 0; i < n; i++) {
					cin>>L1.elem[i];
				}
				L1.length = n;
				break;
			case 3:
				cout<<"输入序列L2的长度："; 
				cin>>n;
				cout<<"输入序列L1：";
				for(i = 0; i < n; i++) {
					cin>>L2.elem[i];
				}
				L2.length = n;
				break;
			case 4:
				cout<<"中位数结果"; 
				cout<<"midValue="<<GetMidValue(L1,L2)<<endl; 
				break;
		}
	}
	return 0;
}

算法的结果：

  

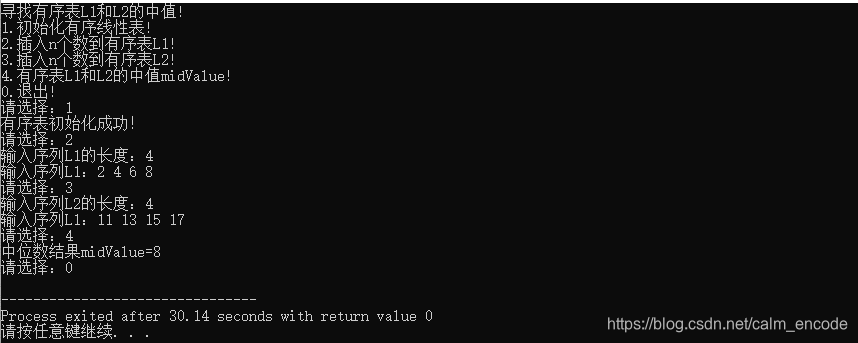
三 算法的时间复杂度与空间复杂度分析

时间复杂度：O(log2^n)；

空间复杂度：根据算法原地工作即算法所需的辅助空间为常量，可以指该算法的空间复杂度为O(1)。