顺藤摸瓜之3D结构光原理

1概述：

如何描述二维相平面中的一个点？

该二维相面，即 三维空间 的一个点

两个船桨位于 水面（二维平面）的点，通过支架（光心），两桨（光机相机）相交于一三维空间点的一点。

水面表示相机面和光机面；

可以想象，船桨交点的任意空间位置，有唯一的 船桨（两桨）水面位置，即两个二维面上的点表示了任意三维的点。

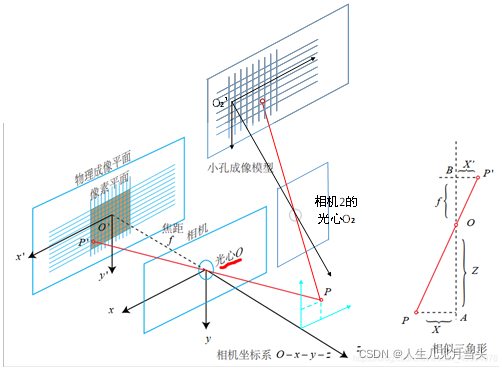
某一固定桨位的侧视图：

 

如何描述空间中的一个点？坐标系、两空间线（矢量）相交

如何确认一条空间线？需要空间中的两个点（像素平面的点和光心）

所在线表示：  p=q +λ v  ；p为组成该线的点，q为起始点，λ为缩放长度，v为向量（u,v,-f）

光心点坐标（0,0,0）（在相机坐标系下），像素平面点（u,v,z）,z=-f，则得到矢量线方向：

(u-0,v-0,-f-0)，即（u,v,-f），则线（上图红色线 PP'）变为

        p(Xc,Yc,Zc)=q(0,0,0)+λ（u,v,-f）

 得到

         (Xc,Yc,Zc)= λ（u,v,-f）

得到

         u=f/Zc *Xc

该结果和小孔成像模型的结果一致。

又立体空间中的两个 空间点到各自坐标原点的线段（即坐标系）可以通过“旋转 R+平移 T”实现（按上面的直线矢量模型，旋转改变v，平移改变q）：

    

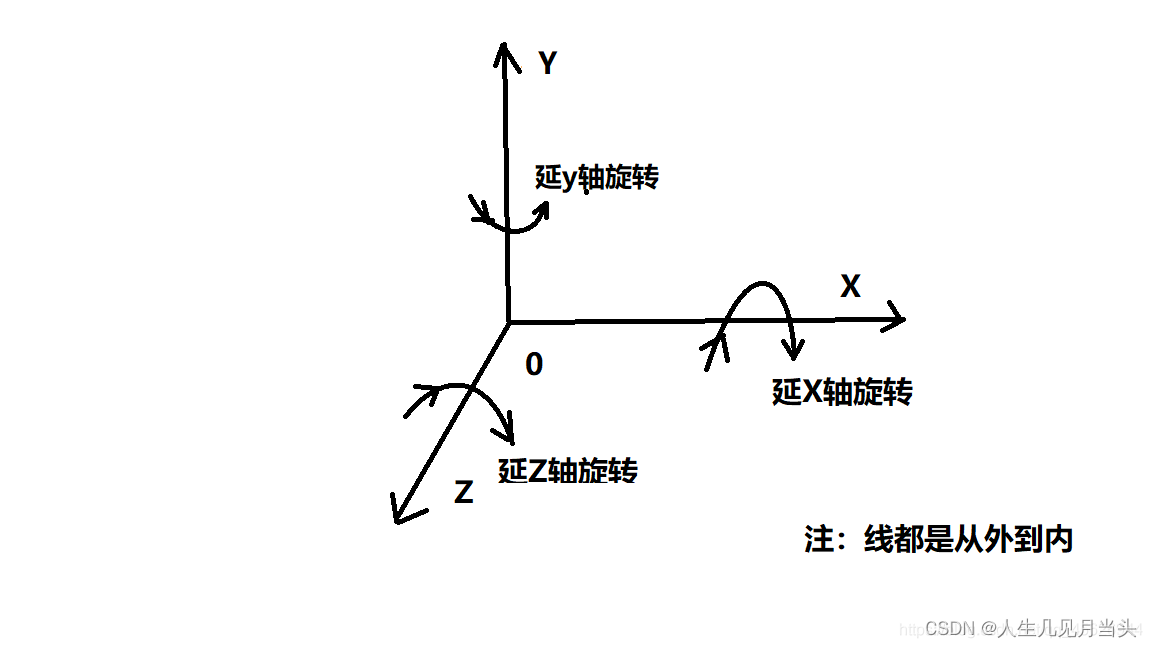
   p(Xc,Yc,Zc,1)=[R T] Pw(Xw,Yw,Zw,1)

代入，得到最终的线描述方程组：

         [R T](Xw,Yw,Zw,1)= λ（u,v,-f,1）

未知数是λ Xw Yw Zw四个，方程只有3个，解不出；从物理意义看，空间中，一条线无法确定一个点，所以有λ 这个自由度 。

引入另一根直线表示： [R2 T2](Xw,Yw,Zw,1)= λ2（u2,v2,-f2,1）

未知数是λ1, λ2, Xw Yw Zw  5个，6个方程，有解。

（为了书写方便，有些数学推论不严谨）

参考文献：

Build Your Own 3D Scanner:
3D Photography for Beginners
 

另一种解释（从维度）：

1概述：

空间点到像素点，要经历3个步骤：

1、最重要：空间点到平面点，相机坐标系到像素平面，三维到二维

2、次重要：空间点到空间点，世界坐标系到相机坐标系，三维到三维：Pc=[R T] Pw

3、次次重要：平面点到平面点，像素平面到理想像素平面，二维到二维（可以先不考虑）

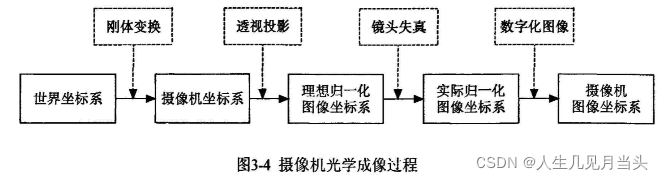
未知数是Zc Xw Yw Zw四个，方程只有3个，解不出。

引入直线2，Zc不一样，但是Xw Yw Zw一样,5个未知数，6个方程，可以解出。

（计算过程中，把Zc消除，方程变为2个，即3个未知数对2个方程；两线则是3个未知数，对应4个方程）

非理想情况，需要考虑像素平面的问题以及镜头的畸变，完善之：

2三维到二维：

针孔相机模型_少杰很帅的博客-优快云博客_小孔相机模型

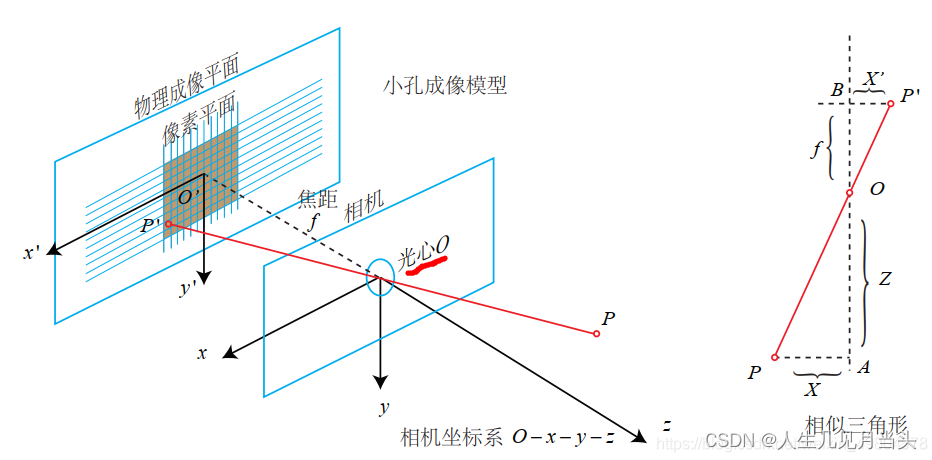
3三维：

相机坐标系和世界坐标系的关系（R和T）：

结论：把P点从相机坐标系改为世界坐标系表示：

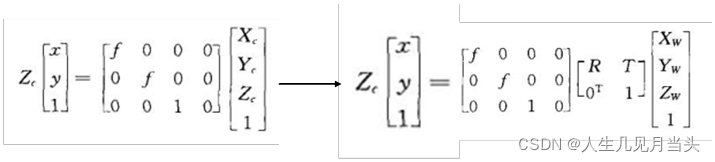
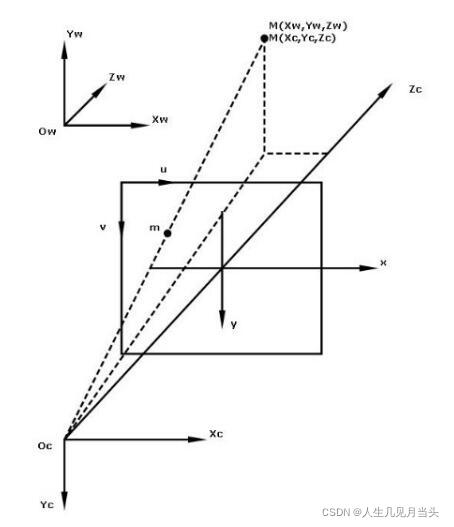
4二维：

像素坐标系和 成像坐标系关系：

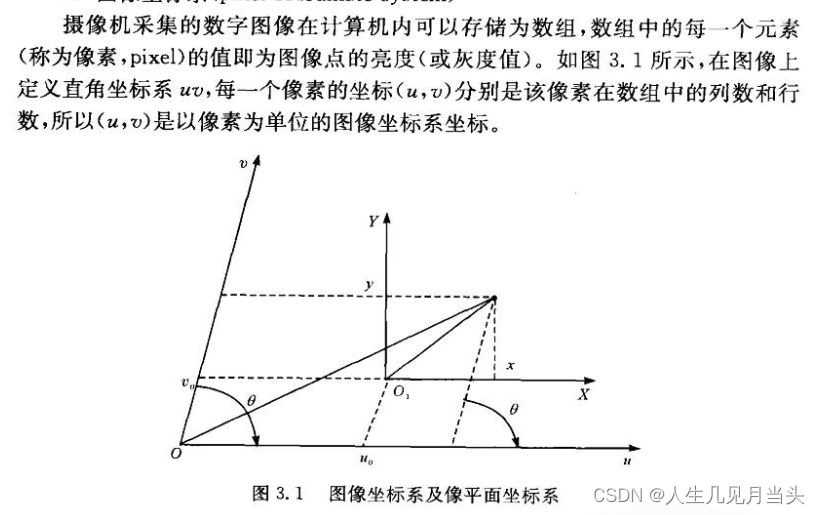
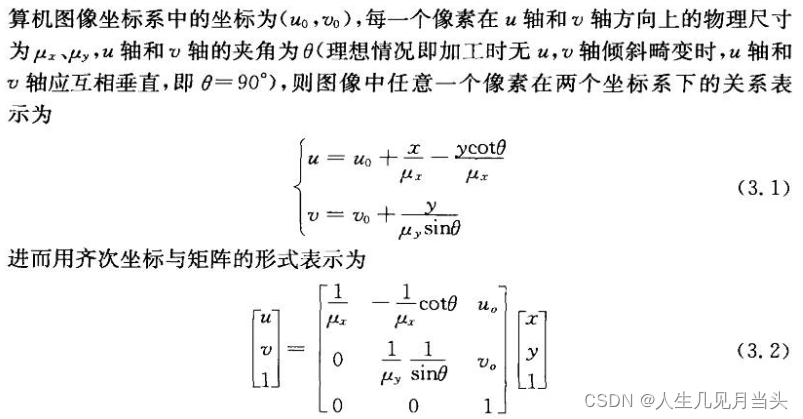
5三个转换综合：

同样的，能得到一个投影仪的式子：

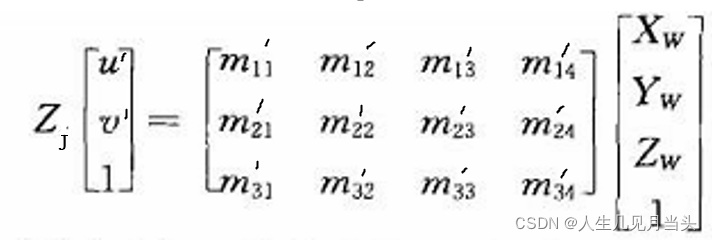
相机一：

未知数是Zc Xw Yw Zw四个，方程只有3个，解不出。

计算过程中，把Zc消除，方程变为2个，即3个未知数对2个方程；两线则未知数3个不变，对应4个方程：

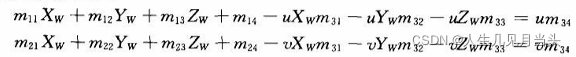
再增加一组相机，即可得到4个方程。

相机二:  得到

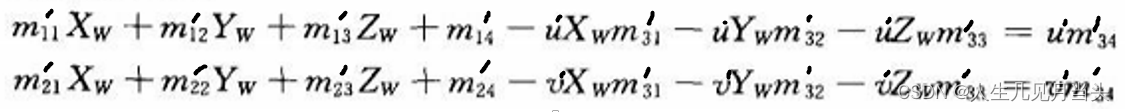
已知M 、M'  、 u 、v 、u' 、 v'，未知： Xw Yw Zw

可求。

以上是双目系统的成像。

（在标定时需要6个点（6x2=12）。用最小二乘法能得求出 m 矩阵12个值。

多点多图可降低误差；）

6 如何将u、v 和u' 、 v'对应？

新的问题是，如何确定XYZ对应到两个相机的点P1和P2 ？

答案是，编码结构光：

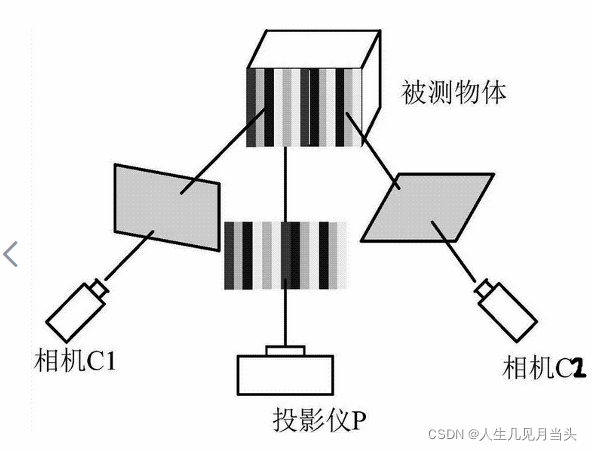
一般的平面图上，确定一点，需要知道行列的位置。比如，22行，18列。

可用二进制表示为：1_0110行，1_0010列

每张图表示1bit，则行列各需要5张图：

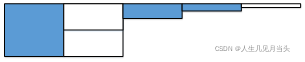
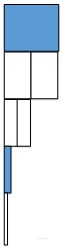
通过类似二进制数的表示方式，每一bit对应一张图，10bit能区分出1024个像素点；

横竖各10张图，则能标记出1024*1024的分辨率。

（为了降低误码率，二进制改成功能一致的编码规则变化的格雷码）

通过相机收到的编码图，就知道相机上某一像素对应的投影仪的像素，从而完成一一对应。

例如，1024*0124的相机，第一个像素位置（1,1），通过解20张图，解出格雷码（3,4），即对应投影仪位置为（3,4）

u=1，v=1，u'=3，v'=4 ；

遍历全图，可以一一对应。

Uc1 、Uprj 、Uc2 三者对应；Vc1 、Vprj 、Vc2也一样。

去除Uc2呢 ？

根据光路可逆，把投影仪当做是相机。

->

单目结构光！

标定cam，得到m，标定prj，得到m’