bfs | [蓝桥杯][历届试题]剪邮票

最新推荐文章于 2022-03-27 12:01:37 发布

原创最新推荐文章于 2022-03-27 12:01:37 发布 · 3.2k 阅读

0 ·

CC 4.0 BY-SA版权

蓝桥杯专栏收录该内容

85 篇文章

订阅专栏

本文详细解析了蓝桥杯竞赛中的经典题目“剪邮票”问题，通过使用广度优先搜索（BFS）算法，计算从12张连在一起的生肖邮票中剪下5张连续邮票的不同方法数量，最终得出正确答案为116种，并提供了完整的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

[蓝桥杯][历届试题]剪邮票

如【图1.jpg】, 有12张连在一起的12生肖的邮票。
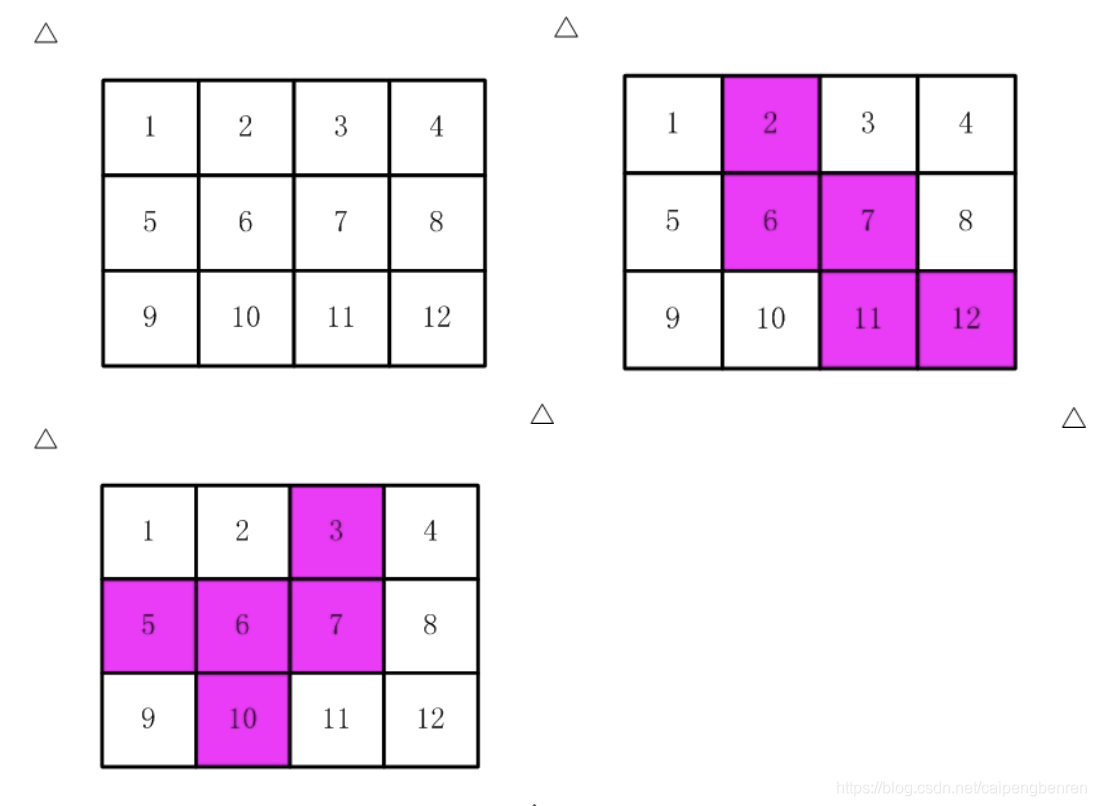
在这里插入图片描述
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

分析：
根据这一题的要求我们可以看出这一题考查的是连通性问题，用bfs，dfs都可以解决，这里我们就使用bfs来解决这个问题。在使用bfs之前，只需要枚举图片中的五个点，在bfs检验是否有连通性为5的答案，有就加一。

答案是 116.

代码如下

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int map[3][4];
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
int bfs(int a, int b) {
    int cnt = 0;
    queue<pair<int, int>> que;
    que.push(make_pair(a, b));
    map[a][b] = 0;
    while(!que.empty()) {
        pair<int ,int > top = que.front();
        que.pop();
        cnt++;
        int x = top.first;
        int y = top.second;
        for(int i = 0; i < 4; i++) {
            int tx = x + dx[i];
            int ty = y + dy[i];
            if (map[tx][ty] == 0 || tx < 0 || tx > 2 || ty < 0 || ty > 3) {
                continue;
            }
            que.push(make_pair(tx, ty));
            map[tx][ty] = 0;
        }
    }
    if (cnt == 5) {
        return 1;
    } else {
        return 0;
    }
}
int main() {
    int ans = 0;
    for (int p1 = 0; p1 <= 7; p1++) {
        for (int p2 = p1 + 1; p2 <= 8; p2++) {
            for (int p3 = p2 + 1; p3 <= 9; p3++) {
                for (int p4 = p3 + 1; p4 <= 10; p4++) {
                    for (int p5 = p4 + 1; p5 <= 11; p5++) {
                        fill(map[0], map[0] + 4 * 5, 0);
                        map[p1 / 4][p1 % 4] = 1;
                        map[p2 / 4][p2 % 4] = 1;
                        map[p3 / 4][p3 % 4] = 1;
                        map[p4 / 4][p4 % 4] = 1;
                        map[p5 / 4][p5 % 4] = 1;
                        ans += bfs(p1 / 4, p1 % 4);
                    }
                }
            }
        }
    }
    cout << ans;
    return 0;
}

相类似的连通性问题：

https://blog.youkuaiyun.com/caipengbenren/article/details/86772283
https://blog.youkuaiyun.com/caipengbenren/article/details/86689035