例[编辑]
计算
把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐,写成以下这种形式:
然后商和余数可以这样计算:
- 将分子的第一项除以分母的最高次项(即次数最高的项,此处为x)。结果写在横线之上(x3 ÷ x = x2).
-
- 将分母乘以刚得到结果(最终商的第一项),乘积写在分子前两项之下(同类项对齐) (x2 · (x − 3) = x3 − 3x2).
-
- 从分子的相应项中减去刚得到的乘积(消去相等项,把不相等的项结合起来),结果写在下面。((x3 − 12x2) − (x3 − 3x2) = −12x2 + 3x2 = −9x2)然后,将分子的下一项“拿下来”。
-
- 把减得的差当作新的被除式,重复前三步(直到余式为零或余式的次数低于除式的次数时为止.被除式=除式×商式+余式 )
-
- 重复第四步。这次没什么可以“拿下来”了。
-
横线之上的多项式即为商,而剩下的 (−123) 就是余数。
算数的长除法可以看做以上算法的一个特殊情形,即所有 x 被替换为10的情形。
/*
* POJ_2527.cpp
*
* Created on: 2013年10月26日
* Author: Administrator
*/
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 10010;
int main(){
int n,k;
int val[maxn];
while(scanf("%d%d",&n,&k)!=EOF,n!=-1 || k !=-1){
int i;
for(i = 0 ; i <= n ; ++i){
scanf("%d",&val[i]);
}
//进行除法运算
for(i = n ; i >= k ; --i){
if(val[i] == 0){
continue;
}
val[i-k] = val[i-k] - val[i];
val[i] = 0;
}
//调整数组长度,即高位的0不用输出
int t = n;
while(val[t] == 0 && t > 0){
--t;
}
for(i = 0 ; i < t ; ++i){
printf("%d ",val[i]);
}
printf("%d\n",val[t]);
}
return 0;
}
 多项式长除法算法
多项式长除法算法





 本文介绍了一种用于计算多项式长除法的算法过程,包括如何通过降幂排列并补零来准备多项式,逐步演示了商和余数的计算步骤。此外,还提供了一个C++实现示例。
本文介绍了一种用于计算多项式长除法的算法过程,包括如何通过降幂排列并补零来准备多项式,逐步演示了商和余数的计算步骤。此外,还提供了一个C++实现示例。

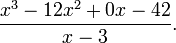


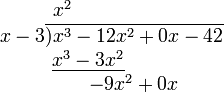
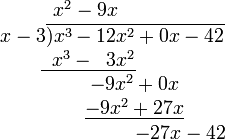
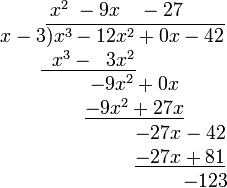


















 902
902

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










