Wasserstein距离在生成模型中的应用

作者丨黄若孜

学校丨复旦大学软件学院硕士生

研究方向丨推荐系统

前言

本文是关于 Wasserstein 距离在生成模型中的应用的一个总结，第一部分讲 Wasserstein 距离的定义和性质，第二部分讲利用 W1 距离对偶性提出的 WGAN ，第三部分包括 ICLR18 的两篇文章，讲不依赖对偶性，可以泛化到利用 W1 距离以外的 Wasserstein 距离来产生生成模型的 WAE，以及用 NN 来模拟 Wasserstein 距离的思想。

Wasserstein距离

衡量两个分布的距离常用的有两种：Optimal Transport 以及 f-divergence（包括 kl 散度，js 散度等）。f-divergence 的定义如下，P 和 Q 是两个不同的分布，则：

其中 f(x) 可以是任何满足 1. f is convex 2. f(1) = 0 的函数。可以证明，当 P 和 Q 完全相同，也就是说取任意的 x，都有 p(x) = q(x)，Df(P||Q)=0。当 P 和 Q 有差异时，由于 f 是 convex 的：

后者等于 0，所以 0 是 f-divergence 的最小值。当 f 取 xlogx 时，得到了 kl 散度。 

而 OT 比 f-divergence 的拓扑更弱，在生成模型中这一点非常重要，因为数据的支撑集往往是输入空间中低维流形 [1]，所以真实分布和生成分布很可能没有重叠，导致 f-divergence 这种捕捉分布的概率密度比的距离会失效（p 和 q 的比值在同一个 x 点计算，而不在意 p(x1)/p(x2) 的大小），从而提供不了有用的信息。

OT 距离也叫 Wasserstein 距离、Earth-Mover（推土机）距离。

1. 定义

Wasserstein 距离定义如下：

其中 ∏(Pr, Pg) 代表 Pr、Pg 所有可能的联合概率分布的集合。γ(x,y) 代表了在 Pr 中出现 x 同时在 Pg 中出现 y 的概率，γ 的边缘分布分别为 Pr 和 Pg。

在这个联合分布下可以求得所有 x 与 y 距离的期望，存在某个联合分布使这个期望最小，这个期望的下确界（infimum）就是 Pr、Pg 的 Wasserstein 距离。

直观上看，如果两个分布是两堆土，希望把其中的一堆土移成另一堆土的位置和形状，有很多种可能的方案。

每一种方案可以对应于两个分布的一种联合概率分布，γ(x,y) 代表了在 Pr 中从 x 的位置移动 γ(x,y) 的土量到 Pg 中的 y 位置，对所有的 x 按 γ 移动，则可将分布 Pr 转化成 Pg。

推土代价被定义为移动土的量乘以土移动的距离，在所有的方案中，存在一种推土代价最小的方案，这个代价就称为两个分布的 Wasserstein 距离。设置 Γ=γ(x,y)，D=||x-y||，其中，则 em 距离可以重写为：

其中 <,>F 为内积符号。

2. Kantorovich-Rubinstein Duality

当 D=||x-y|| 时，找 Wasserstein 距离的问题其实是一个线性规划的问题。线性规划问题是指在线性的约束条件下找一个线性目标函数的最优化解（极大解或者极小解）。包括三个部分：

• 一个需要极大化的线性函数

    

• 以下形式的问题约束：

  
  

• 非负变量

 

在本问题中，可以将 Γ 和 D 两个矩阵展成一维：x = vec(Γ), c = vec(D)。找到 x 以最小化代价，其中。同时 x 需要满足约束条件 Ax = b，其中,, x≥0。其中，m = 2l。

为了得到这个约束条件，令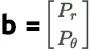。A 则需要设置为 m*n 的矩阵，挑出 x 中适当位置的值得到两个边缘分布。

如果像本问题中，随机变量只有一维，在这个维度上有有限个离散的状态，可以直接用解线性规划问题的方式来求解。然而在解实际问题中，比如学习图片的分布时，随机变量有上千个维度，直接计算几乎是不可能的。

但是由于我们需要的只是 z 的最小值，并且利用 z 求出生成分布 Pθ ，而不一定需要求出 x(Γ)。所以我们可以对 z 进行关于 Pθ 的梯度下降