一文详解神经网络与激活函数的基本原理

©PaperWeekly 原创 · 作者｜王东伟

单位｜致趣百川

研究方向｜深度学习

本文介绍神经网络（Neural Network）及激活函数（Activation Function）的基本原理。

考虑以下分类问题：

▲ 图1

显然，该分类问题具有非线性的决策边界。如果不增加特征，采用线性核的 SVM（以下简称线性 SVM）和逻辑回归都无法拟合，因为它们只能得到形如 的线性边界。

一个可行的办法是增加高次方项作为特征输入，比如以 作为线性 SVM 或逻辑回归输入，可以拟合形如 的决策边界（实际上它可以拟合圆或椭圆），对于图 1 所示的例子这可能是不错的模型。

然而，在实际案例中我们通常都无法猜到决策边界的“形状”，一是因为样本的特征数量很大导致无法可视化，二是其可能的特征组合很多。

对于上述非线性模型拟合的问题，我们之前介绍了采用核函数的 SVM，本文将介绍更通用的方法——神经网络。

考虑以下矩阵运算：

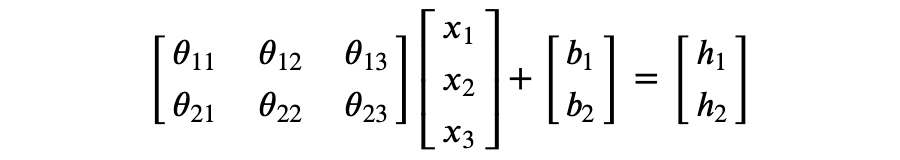
即：

可以看到   的每个元素都是