大厂面试必考动态规划算法问题汇总：终极详解+分析+归纳 dp动态规划问题大全解 + 所有常考题型总结思路

动态规划算法全览
原创 已于 2025-07-28 01:20:52 修改 · 1.4k 阅读 · 17 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#动态规划 #算法 #嵌入式硬件 #c语言 #面试 #职场和发展 #数据结构

于 2025-07-21 23:34:29 首次发布

引子 ：动态规划硬核之路所有个人源码分享+解题过程共享（0）

最近搞完了dp动态规划问题+贪心算法问题，这里是所有题型的全览：

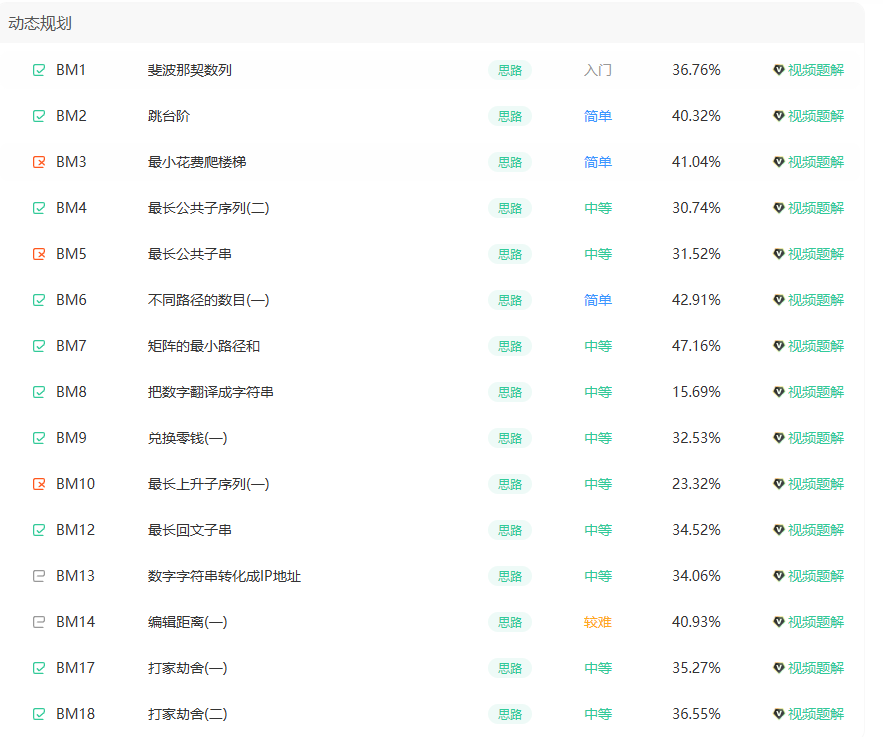
以下是值得思考、值得反复练习的经典动态规划算法问题！！！
 

一共10道题

1  最长公共子序列：

2  最长公共子串：

#3刷 2025/7/15

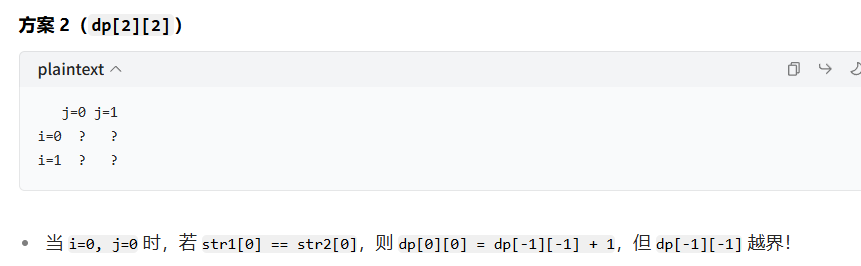
这里变成了：dp[i][j] = dp[i-1][j-1]+1就是回越界

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * longest common substring
 * @param str1 string字符串 the string
 * @param str2 string字符串 the string
 * @return string字符串
 */
#include <stdio.h>

char *LCS(char *str1, char *str2)
{
    // write code here
    // int l1 =strlen(str1);
    // int l2 = strlen(str2);
    // if(l1==0 || l2 ==0 ){
    //     return NULL;
    // }
    // int Max = 0,end = 0;
    // int dp[5001][5001] = {0};
    // for(int i =1 ;i<=l1;i++){
    //     for(int j=1;j<=l2;j++){
    //         if(str1[i-1]==str2[j-1]){
    //             dp[i][j]=dp[i-1][j-1]+1;
    //             if(dp[i][j]>Max){
    //                 end = i-1;
    //                 Max = dp[i][j] ;
    //             }
    //         }
    //         else{
    //             dp[i][j]=0;
    //         }
    //     }
    // }
    // //存到了产犊Max  end结束的位置
    // char* res = (char* )malloc(sizeof(char)*3000);
    // for(int i = 0;i<Max;i++){
    //     res[i]= str1[end-Max+1+i];
    // }
    // res[Max]='\0';
    // return res;

    // #2刷
    // 最长公共子串,两个位置的必须相同，不然直接跳过为0
    // int len1 = strlen(str1) , len2 = strlen(str2);
    // int dp[len1+1][len2+1] ;
    // dp[0][0] = 0 ;
    // int maxLen = 0;
    // int endPos = 0;
    // for(int i=1;i<=len1;i++){
    //     for(int j =1;j<=len2;j++){
    //         if(str1[i-1]==str2[j-1]){
    //             dp[i][j] = dp[i-1][j-1]+1;
    //             if(dp[i][j]>maxLen){
    //                 endPos = i;
    //                 maxLen = dp[i][j];
    //             }
    //         }
    //         else{
    //             dp[i][j]=0;
    //         }
    //     }
    // }
    // endPos-=1;
    // char* res = (char*)malloc(5001*sizeof(char));
    // for(int i = 0;i<maxLen;i++){
    //     res[i] = str1[endPos-maxLen+i];
    // }
    // res[maxLen] = '\0';
    // return res;

    // #3刷
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    int **dp = (int **)malloc((len1 + 1) * sizeof(int *));
    for (int i = 0; i <= len1; i++)
    {
        dp[i] = (int *)calloc((len2 + 1), sizeof(int));
    }
    int maxLen = 0;
    int end = 0;
    for (int i = 1; i <= len1; i++)
    {
        for (int j = 1; j <= len2; j++)
        {
            if (str1[i - 1] == str2[j - 1])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
                if (dp[i][j] > maxLen)
                {
                    maxLen = dp[i][j];
                    // #vip 容易错
                    end = i - 1;
                }
            }
            else
            {
                dp[i][j] = 0;
            }
        }
    }
    // 处理这个start ->end 的序列：
    int start = end - maxLen + 1;
    char *res = (char *)malloc(5000 * sizeof(char));
    for (int i = 0; i < maxLen; i++)
    {
        res[i] = str1[start + i];
    }
    res[maxLen] = '\0';
    return res;
}

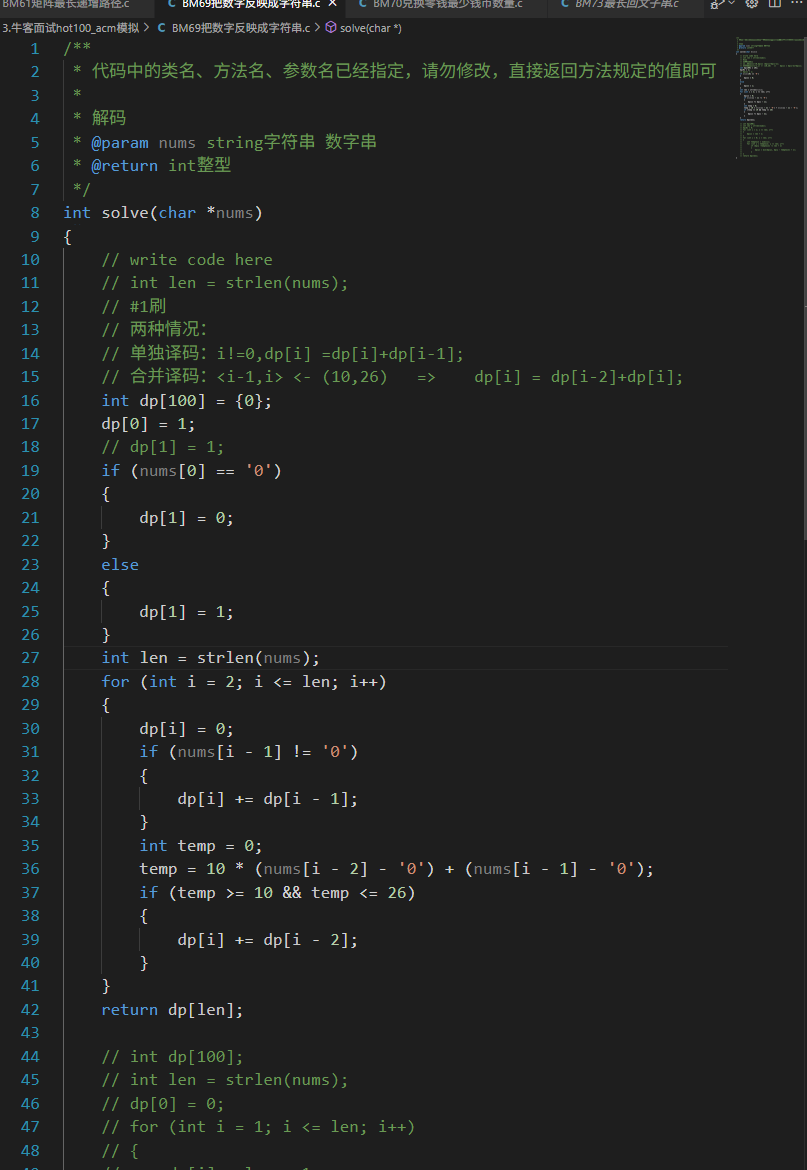
3 数字翻译成字符串？

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 解码
 * @param nums string字符串 数字串
 * @return int整型
 */
int solve(char *nums)
{
    // write code here
    // int len = strlen(nums);
    // #1刷
    // 两种情况：
    // 单独译码：i!=0,dp[i] =dp[i]+dp[i-1];
    // 合并译码：<i-1,i> <- (10,26)   =>    dp[i] = dp[i-2]+dp[i];
    int dp[100] = {0};
    dp[0] = 1;
    // dp[1] = 1;
    if (nums[0] == '0')
    {
        dp[1] = 0;
    }
    else
    {
        dp[1] = 1;
    }
    int len = strlen(nums);
    for (int i = 2; i <= len; i++)
    {
        dp[i] = 0;
        if (nums[i - 1] != '0')
        {
            dp[i] += dp[i - 1];
        }
        int temp = 0;
        temp = 10 * (nums[i - 2] - '0') + (nums[i - 1] - '0');
        if (temp >= 10 && temp <= 26)
        {
            dp[i] += dp[i - 2];
        }
    }
    return dp[len];

    // int dp[100];
    // int len = strlen(nums);
    // dp[0] = 0;
    // for (int i = 1; i <= len; i++)
    // {
    //     dp[i] = len + 1;
    // }
    // for (int i = 0; i < len; i++)
    // {
    //     int tempCoin = nums[i];
    //     for (int j = tempCoin; j <= len; j++)
    //         if (dp[j -tempCoin] != len + 1)
    //         {
    //             dp[j] = min(dp[j], dp[j - tempCoin] + 1);
    //         }
    // }
    // return dp[len];
}

关键：

（1）第一种情况：a[i]!=0
   (2) 第二章情况：a[i]<(10,26)

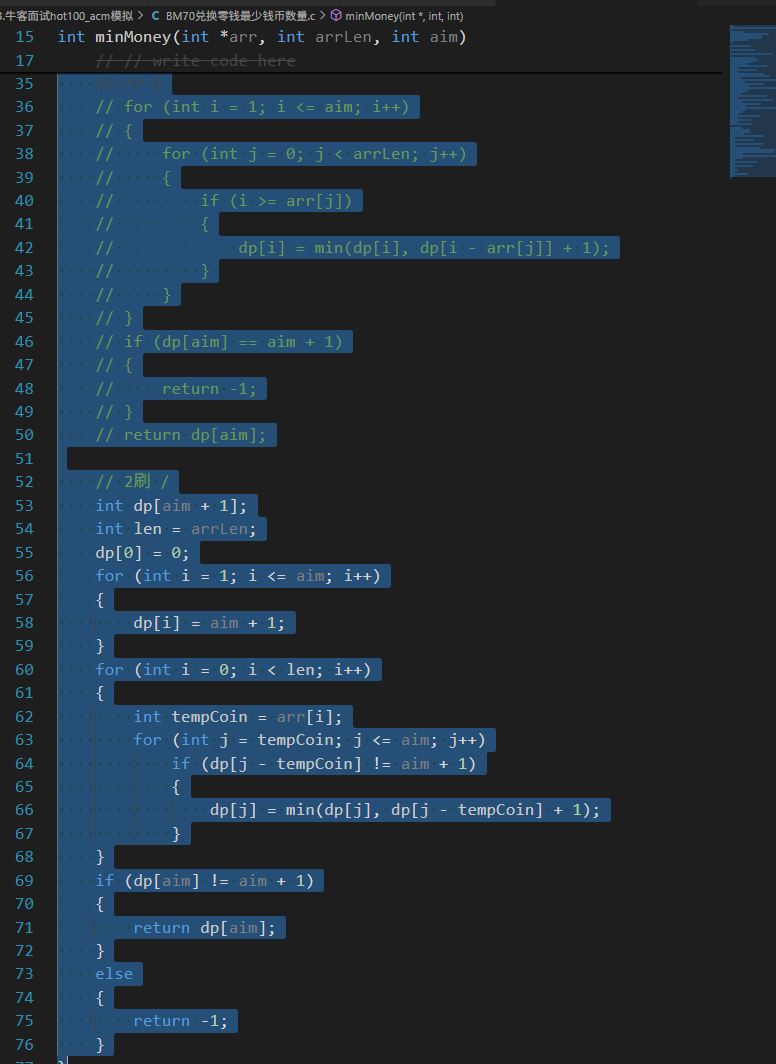
4 兑换零钱？

遍历所有的1->len长度的序列的每一个硬币面值：
       如果dp[j-coin]!=aim+1 那么更新整个dp[j]的值

比如【5，2，3】 20

 第一轮，从5>>>20,更新的有：dp[5] dp[10] dp[15] dp[20]


 

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 最少货币数
 * @param arr int整型一维数组 the array
 * @param arrLen int arr数组长度
 * @param aim int整型 the target
 * @return int整型
 */

int min(int a, int b)
{
    return a < b ? a : b;
}
int minMoney(int *arr, int arrLen, int aim)
{
    // // write code here
    // int maxLen = aim + 1;
    // int dp[aim + 1];
    // dp[0] = 0;
    // for (int i = 1; i <= aim; i++)
    // {
    //     dp[i] = aim + 1;
    // }
    // // 随你怎么变 总会比aim+1小
    // // for (int i = 1; i <= aim; i++)
    // // {
    // //     for (int j = 0; j < arrLen; j++)
    // //     {
    // //         if (i >= arr[j])
    // //         {
    // //             dp[i] = min(dp[i], dp[i - arr[j]] + 1);
    // //         }
    // //     }
    // // }
    // for (int i = 1; i <= aim; i++)
    // {
    //     for (int j = 0; j < arrLen; j++)
    //     {
    //         if (i >= arr[j])
    //         {
    //             dp[i] = min(dp[i], dp[i - arr[j]] + 1);
    //         }
    //     }
    // }
    // if (dp[aim] == aim + 1)
    // {
    //     return -1;
    // }
    // return dp[aim];

    // 2刷 /
    int dp[aim + 1];
    int len = arrLen;
    dp[0] = 0;
    for (int i = 1; i <= aim; i++)
    {
        dp[i] = aim + 1;
    }
    for (int i = 0; i < len; i++)
    {
        int tempCoin = arr[i];
        for (int j = tempCoin; j <= aim; j++)
            if (dp[j - tempCoin] != aim + 1)
            {
                dp[j] = min(dp[j], dp[j - tempCoin] + 1);
            }
    }
    if (dp[aim] != aim + 1)
    {
        return dp[aim];
    }
    else
    {
        return -1;
    }
}

5 最长回文？

#include <stdio.h>
#include <math.h>
#include <string.h>
// int doFunc(char *A, int left, int right)
// {
//     // 从left和right开始一个个往两边拓展，用一个cnt计数
//     // int len = strlen(A);
//     // int cnt = 0, flag = 0;
//     // if (left == right)
//     // {
//     //     cnt = 1;
//     //     left--;
//     //     right++;
//     // }
//     // while (A[left] == A[right] && left >= 0 && right < len)
//     // {
//     //     cnt += 2;
//     //     left--;
//     //     right++;
//     // }
//     // return cnt;

//     //最开始一个都没有，绝对是0
//     int res =0;
//     //中间相等bab 、 不相等baab
//     if(left==right){
//         res =1;
//         left-=1;
//         right+=1;
//     }
//     // int len  = strLen(A);
//     int len = strlen(A);
//     while(A[left]==A[right] &&  left>=0 && right<len ){
//         res+=2;
//         left-=1;right+=1;
//     }
//     return res;
// }

// int max(int a, int b)
// {
//     return a > b ? a : b;
// }

// int getLongestPalindrome(char *A)
// {
//     // write code here
//     // dp方法：初始状态 - 装填转移 - 边界条件

//     // 干活的函数： s , left , right
//     // mid 开始，left -1 ,right+1 向两边拓展
//     // 主函数，从0到右边，一个个找，
//     // #self 从左边开始一个个找
//     // int maxLen = 1;
//     // int len = strlen(A);
//     // if (len == 0)
//     // {
//     //     return 0;
//     // }
//     // int r1, r2;
//     // for (int i = 0; i < len; i++)
//     // {
//     //     r1 = doFunc(A, i, i);
//     //     r2 = doFunc(A, i, i + 1);
//     //     int res = max(r1, r2);
//     //     if (res > maxLen)
//     //     {
//     //         maxLen = res;
//     //     }
//     // }
//     // return maxLen;

//     int maxLen = 1;
//     int len = strlen(A);
//     for(int i =0;i<len;i++){
//         int res1= doFunc(A,i,i);
//         int res2 = doFunc(A,i,i+1);
//         int res = max(res1,res2);
//         if(res>maxLen) maxLen =res;
//     }
//     return maxLen;
}

// 3刷

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 *
 * @param A string字符串
 * @return int整型
 */
int max(int a, int b)
{
    return a > b ? a : b;
}

int doFunc(char *a, int len, int left, int right)
{
    while (left >= 0 && right < len && a[left] == a[right])
    {
        left--;
        right++;
    }
    return right - left - 1;
}

int getLongestPalindrome(char *A)
{
    // write code here

    if (!A)
        return -1 + 1;
    int len = strlen(A);
    if (len == 1)
    {
        return 1;
    }
    int maxLen = 1;
    for (int i = 0; i < len; i++)
    {
        int len1 = doFunc(A, len, i, i);
        int len2 = doFunc(A, len, i, i + 1);
        int tempM = max(len1, len2);
        if (tempM > maxLen)
        {
            maxLen = tempM;
        }
    }
    return maxLen;
}

6 最长上升子序列？

// #include <stdio.h>

// int main()
// {
//     int arr[] = {47, 89, 23, 76, 12, 55, 34, 91, 62, 7, 38, 81, 44, 50, 99};
//     printf("最长上升子序列是：%d\n\n", LTS(arr, 15));
//     printf("最长上升子序列是\n");
//     return 0;
// }

// int LTS(int *arr, int arrLen)
// {
//     int dp[arrLen];
//     if (arrLen == 0)
//     {
//         return 0;
//     }
//     for (int i = 0; i < arrLen; i++)
//     {
//         dp[i] = 1;
//     }
//     dp[0] = 1;
//     int maxLen = 1;
//     // for (int i = 1; i < arrLen; i++)
//     // {
//     //     for (int j = 0; j < i; j++)
//     //     {
//     //         if (arr[i] > arr[j])
//     //         {
//     //             if (dp[j] + 1 > dp[i])
//     //             {
//     //                 dp[i] = dp[j] + 1;
//     //             }
//     //         }
//     //     }
//     //     if (dp[i] > maxLen)
//     //     {
//     //         maxLen = dp[i];
//     //     }
//     // }
//     for(int i =1;i<arrLen;i++){
//         for(int j = 0 ;j<i;j++){
//             if(arr[i]>arr[j]){
//                 if(dp[j]+1>dp[i]){
//                     dp[i] = dp[j]+1;
//                 }
//             }
//         }
//         if(dp[i]>maxLen ){
//             maxLen = dp[i];
//         }
//     }
//     return maxLen;
// }

# 2刷

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 给定数组的最长严格上升子序列的长度。
 * @param arr int整型一维数组 给定的数组
 * @param arrLen int arr数组长度
 * @return int整型
 */
int LIS(int *arr, int arrLen)
{
    // write code here
    if (!arr)
    {
        return 0;
    }
    int dp[arrLen];
    for (int i = 0; i < arrLen; i++)
    {
        dp[i] = 1;
    }
    int maxLen = 1;
    for (int i = 0; i < arrLen; i++)
    {
        for (int j = 0; j < i; j++)
        {
            if (arr[j] < arr[i])
            {
                dp[i] = max(dp[i], dp[j] + 1);
                maxLen = max(maxLen, dp[i]);
            }
            else
            {
                // dp[i] = dp[j];
                ;
            }
        }
    }

    // return dp[arrLen - 1];
    return maxLen;
}

dp[i] dp[j] 的动态规划：

0-》arrlen 
    0->i

        如果大，
                  dp[i] = 挑一个大的

                   记录一下


7   字符串转化ip地址？

8 编辑距离？

9 打家劫舍（1）+（2）？

20257.20三刷！

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 *
 * @param nums int整型一维数组
 * @param numsLen int nums数组长度
 * @return int整型
 */

#define MaxV 15000

typedef struct Person
{
    char name[];
    int age;
} chinese;

#include <stdio.h>
int max(int a, int b)
{
    return a > b ? a : b;
}
int rob(int *nums, int numsLen)
{
    // write code here
    // 打家劫舍问题：要么搞nums[i]+dp[i-2] ,要么dp[i-1]
    // int dp[numsLen] ;
    // dp[1] =max(nums[0],nums[1]);
    // dp[0] = nums[0];
    // for(int i=2;i<numsLen;i++){
    //     dp[i] = max(dp[i-1],nums[i]+dp[i-2]);
    // }
    // return dp[numsLen-1];

    // 2刷
    char* a[];
    int b[100];
    int* ptr_Int = b;

    if (!nums || numsLen == 0)
    {
        return 0;
    }
    if (numsLen == 1)
    {
        return nums[0];
    }
    if (numsLen == 2)
    {
        return max(nums[0], nums[1]);
    }
    int dp[numsLen];
    for (int i = 2; i < numsLen; i++)
    {
        dp[i] = 0;
    }
    for (int i = 2; i < numsLen; i++)
    {
        dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
    }
    return dp[numsLen - 1];
}

// int main(){
//     int a[] = {12, 9,6,6,7,7,4,5,3,7,3,3,7,5,23,6,2,36,26,4,23,6,2,36,24,36,3,68,8 ,12};
//     int len = sizeof(a)/sizeof(a[0]);
//     printf("结果是：%d \n",rob(a,len));
// }

环形：


int max(int a, int b)
{
    return a > b ? a : b;
}

int rob(int *nums, int numsLen)
{
    int dp1[numsLen];
    int dp2[numsLen];
    int m1 = 0;
    int m2 = 0;
    // 第一家偷，最后一个不能偷！
    // 1st不，last one 可以！
    dp1[0] = nums[0];
    dp1[1] = dp1[0];
    for (int i = 2; i < numsLen - 1; i++)
    {
        dp1[i] = max(dp1[i - 2] + nums[i], dp1[i - 1]);
    }
    m1 = dp1[numsLen - 2];

    dp2[0] = 0;
    dp2[1] = nums[1];
    for (int i = 2; i < numsLen; i++)
    {
        dp2[i] = max(dp2[i - 2] + nums[i], dp2[i - 1]);
    }
    m2 = dp2[numsLen - 1];

    return max(m1, m2);
}

以上是笔记本手写的思维分析+总结

---------------------------------------------------------------------------------------------------------最近更新于2025.7.21 晚上1：00
 

1 x做过了就会，你不看试试?

2 多回顾题目！
3 脑子过 反复

---------------------------------------------------------------------------------------------------------------------重制版>>>>>更新于2025.7.22晚上10：00

动态规划硬核之路：从最长公共子串到数字翻译（第一部分）

前言：DP，嵌入式面试的“拦路虎”还是“敲门砖”？

兄弟们，咱们搞嵌入式的，C语言是基本功，但算法，特别是动态规划，那绝对是面试大厂的“分水岭”。很多人觉得DP难，无从下手，但我告诉你，DP不是玄学，它有套路，有思想。一旦你掌握了它，它就会从“拦路虎”变成你进入大厂的“敲门砖”！

我大学四年学嵌入式，研究生搞了几年区块链，现在又回来刷C语言准备嵌入式工作，深知这种“半路出家”的痛苦。但正是这种经历，让我对知识的理解更深了一层：基础，永远是王道！ 而DP，正是检验你基础功底和逻辑思维能力的绝佳利器。

这篇博客，我将结合我在牛客、力扣上刷题的真实代码，手把手带你剖析DP问题的核心，从最基本的概念讲起，深入浅出，力求让每一个看过100道热题榜的C程序员都能看懂，都能有所收获。

1 动态规划初探：核心思想与基本要素

在深入具体题目之前，咱们先来聊聊动态规划到底是个啥。

动态规划 (Dynamic Programming, DP)，简单来说，就是把一个复杂的大问题，拆分成若干个相互关联的子问题，通过解决这些子问题，并把子问题的解存储起来（避免重复计算），最终得到大问题的解。

它的核心思想就俩字：“重叠子问题” 和 “最优子结构”。

  • 重叠子问题 (Overlapping Subproblems)：解决大问题时，会反复遇到相同的子问题。DP通过记忆化（Memoization）或填表（Tabulation）来存储子问题的解，避免重复计算，大大提高效率。

  • 最优子结构 (Optimal Substructure)：大问题的最优解可以通过子问题的最优解来构造。这意味着，如果你能找到子问题的最优解，那么把它们组合起来就能得到整个问题的最优解。

构建一个DP解决方案，通常需要明确以下几个要素：

  1. DP 状态定义：dp[i] 或 dp[i][j] 代表什么？这是最关键的一步，定义好了，后面就水到渠成了。

  2. DP 状态转移方程：dp[i] 或 dp[i][j] 如何从之前的状态推导出来？这是DP的核心逻辑。

  3. 初始化：DP 数组的初始值是多少？通常是边界条件，或者一些特殊情况。

  4. 边界条件：最小的子问题是什么？它们的解是什么？

  5. 计算顺序：是自底向上（填表法）还是自顶向下（记忆化搜索）？通常填表法更常见。

我们可以用一张思维导图来概括DP的核心要素：

DP核心要素

描述

常见表现形式

状态定义

dp[i] 或 dp[i][j] 表示什么？

数组、二维数组

转移方程

如何从已知状态推导出当前状态？

dp[i] = f(dp[i-1], dp[i-2], ...)

初始化

最小子问题的解，或数组的起始值。

dp[0] = ..., dp[0][0] = ...

边界条件

问题的最小规模，或特殊情况的处理。

i=0 或 j=0 时的情况

计算顺序

遍历方向，确保计算当前状态时所需的前置状态已计算。

通常是嵌套循环，从小到大遍历 i 和 j

2 经典问题剖析：最长公共子串 (Longest Common Substring)

好了，理论说完了，咱们直接上硬菜！第一个要讲的，就是最长公共子串。用户在代码里把它写成了 LCS，但从实现来看，它确实是最长公共子串，而不是最长公共子序列。这里咱们先明确一下概念：

  • 最长公共子串 (Longest Common Substring)：两个字符串中，最长的连续的公共部分。例如 "ABCDE" 和 "ABFCE"，最长公共子串是 "AB"。

  • 最长公共子序列 (Longest Common Subsequence)：两个字符串中，最长的非连续的公共部分（保持相对顺序）。例如 "ABCDE" 和 "ABFCE"，最长公共子序列是 "ABCE"。

这两个问题虽然名字相似，但DP状态转移方程有本质区别。咱们先聚焦最长公共子串。

问题描述

给定两个字符串 str1 和 str2，找出它们的最长公共子串。

用户代码分析与思考

我们先来看看用户提供的LCS函数（实际是最长公共子串）的代码：

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * longest common substring
 * @param str1 string字符串 the string
 * @param str2 string字符串 the string
 * @return string字符串
 */
#include <stdio.h>
#include <string.h> // 补充头文件
#include <stdlib.h> // 补充头文件

char *LCS(char *str1, char *str2){
    // write code here
    // #3刷
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    // 动态分配二维数组，避免栈溢出，尤其是在大字符串时
    int **dp = (int **)malloc((len1 + 1) * sizeof(int *));
    for (int i = 0; i <= len1; i++)
    {
        // calloc 会自动将内存初始化为0，非常适合DP数组
        dp[i] = (int *)calloc((len2 + 1), sizeof(int));
    }

    int maxLen = 0; // 记录最长公共子串的长度
    int end = 0;    // 记录最长公共子串在str1中的结束位置（索引）

    for (int i = 1; i <= len1; i++)
    {
        for (int j = 1; j <= len2; j++)
        {
            // 如果当前字符匹配
            if (str1[i - 1] == str2[j - 1])
            {
                // 状态转移：当前公共子串长度等于前一个字符匹配时的长度加1
                dp[i][j] = dp[i - 1][j - 1] + 1;
                // 更新最大长度和结束位置
                if (dp[i][j] > maxLen)
                {
                    maxLen = dp[i][j];
                    // #vip 容易错：end记录的是str1中子串的结束索引
                    // 因为i是基于1的索引，str1[i-1]是当前字符，所以i-1就是当前字符的索引
                    end = i - 1;
                }
            }
            else
            {
                // 如果当前字符不匹配，则公共子串断开，长度重置为0
                dp[i][j] = 0;
            }
        }
    }

    // 处理这个start ->end 的序列：
    // 根据最长子串的长度和结束位置，计算起始位置
    int start = end - maxLen + 1;
    // 分配结果字符串内存，maxLen + 1 用于存放 '\0'
    char *res = (char *)malloc((maxLen + 1) * sizeof(char));
    if (res == NULL) { // 内存分配失败检查
        // 释放之前分配的dp内存
        for (int i = 0; i <= len1; i++) {
            free(dp[i]);
        }
        free(dp);
        return NULL; // 返回错误
    }

    // 复制子串到结果字符串
    for (int i = 0; i < maxLen; i++)
    {
        res[i] = str1[start + i];
    }
    res[maxLen] = '\0'; // 添加字符串结束符

    // 释放动态分配的dp内存，避免内存泄漏
    for (int i = 0; i <= len1; i++)
    {
        free(dp[i]);
    }
    free(dp);

    return res;
}

我的分析和思考：

用户这份代码已经是第三次刷了，进步非常明显！从注释的 #3刷于7/15 和 #vip 容易错 都能看出，用户在思考和解决问题过程中遇到的困惑和进步。

优点：

  1. DP 状态定义清晰：dp[i][j] 表示以 str1[i-1] 和 str2[j-1] 结尾的最长公共子串的长度。这个定义非常关键，因为它直接决定了状态转移方程。

  2. 状态转移方程正确：if (str1[i-1] == str2[j-1]) { dp[i][j] = dp[i-1][j-1] + 1; } else { dp[i][j] = 0; } 完美体现了子串连续性的要求。

  3. 动态分配 dp 数组：用户从之前的固定大小数组 int dp[5001][5001] 改为 malloc 动态分配，这是一个巨大的进步！避免了栈溢出，使得代码能处理更长的字符串。

  4. calloc 初始化：使用 calloc 自动初始化为0，省去了手动清零的步骤，代码更简洁。

  5. 记录 maxLen 和 end：能够正确地记录最长公共子串的长度和其在 str1 中的结束位置，这是构建结果字符串的关键。

可以优化和改进的地方：

  1. 头文件缺失：strlen, malloc, free 都需要 <string.h> 和 <stdlib.h>。虽然在某些IDE或编译器下可能隐式包含，但为了代码的健壮性和可移植性，必须显式包含。

  2. malloc 大小：在 char* res = (char* )malloc(sizeof(char)*3000); 或 char* res = (char*)malloc(5001*sizeof(char)); 处，虽然用户在第三次刷的时候改成了 5000 * sizeof(char)，但更精确和安全的做法是根据 maxLen 来分配，即 (maxLen + 1) * sizeof(char)，因为 maxLen 可能远小于5000，造成内存浪费；也可能在极端情况下 maxLen 超过5000，导致内存不足。

  3. 内存泄漏：在返回 res 之前，需要 free 掉之前 malloc 出来的 dp 数组。用户在第三次刷的时候已经考虑到了这一点，并在返回前释放了 dp 数组，非常棒！

  4. 边界条件处理：虽然代码中 if(len1==0 || len2 ==0 ) 的注释部分被删除了，但对于空字符串的输入，最好在函数开头进行显式检查，避免后续操作出现空指针解引用。

深入浅出：最长公共子串的DP原理与实现

咱们来彻底捋一遍最长公共子串的DP思路。

1. DP 状态定义：

dp[i][j] 表示以 str1[i-1] 结尾且以 str2[j-1] 结尾的最长公共子串的长度。 注意这里的 i 和 j 是为了方便DP数组的索引，它们分别对应 str1 和 str2 的前 i 个和前 j 个字符。所以实际字符索引是 i-1 和 j-1。

2. DP 状态转移方程：

  • 如果 str1[i-1] == str2[j-1] (当前字符匹配)： dp[i][j] = dp[i-1][j-1] + 1 这意味着，如果当前字符匹配，那么最长公共子串的长度就是它们前一个字符匹配时的长度加1。

  • 如果 str1[i-1] != str2[j-1] (当前字符不匹配)： dp[i][j] = 0 因为是“子串”，要求连续，一旦不匹配，公共子串就断了，长度自然归零。

3. 初始化：

  • dp[0][j] = 0 (当 str1 为空时，没有公共子串)

  • dp[i][0] = 0 (当 str2 为空时，没有公共子串)

  • 由于我们使用 calloc 动态分配并初始化为0，这些边界条件自然满足。

4. 计算顺序：

从 i = 1 到 len1，从 j = 1 到 len2，双重循环遍历。

DP 状态表（以 str1 = "ABCDE", str2 = "ABFCE" 为例）：

""

A=0

B=1

F=2

C=3

E=4

""

0

0

0

0

0

0

A=0

0

1

0

0

0

0

B=1

0

0

2

0

0

0

C=2

0

0

0

0

1

0

D=3

0

0

0

0

0

0

E=4

0

0

0

0

0

1

解释：

最低0.47元/天 解锁文章
动态规划算法面试必刷50题（附详细题解）
AI 算法实战派
05-29 1128
本文专为“面试突击动态规划”的程序员设计，目标是用最短时间掌握DP的核心解题框架，并通过10道高频题（覆盖LeetCode Top 50%的DP考点）形成“条件反射”——看到题目能快速判断是否用DP、如何定义状态、如何推导转移方程。用“爬楼梯”故事理解DP的核心三要素（重叠子问题、最优子结构、状态转移）总结DP解题的“四步黄金法则”（状态定义→转移方程→初始化→填表顺序）拆解5类高频题型，精选10道必刷题（含LeetCode题号+难度+题解）总结面试避坑指南和练习策略。
到底什么是dp思想（内含大量经典例题，附带详细解析）
热门推荐
Y先森0.0
06-23 6万+
&#13; 期末了，通过写博客的方式复习一下dp，把自己理解的dp思想通过样例全部说出来说说我所理解的dp思想dp一般用于解决多阶段决策问题，即每个阶段都要做一个决策，全部的决策是一个决策序列，要你求一个最好的决策序列使得这个问题有最优解将待求解的问题分为若干个相互联系的子问题，只在第一次遇到的时候求解，然后将这个子问题的答案保存下来，下次又遇到的时候直接拿过来用即可dp和分...
HDU 动态规划（46道题目）倾情奉献~ 【只提供思路与状态转移方程】
遇见_缘
02-22 4794
Robberies http://acm.hdu.edu.cn/showproblem.php?pid=2955     背包;第一次做的时候把概率当做背包(放大100000倍化为整数):在此范围内最多能抢多少钱  最脑残的是把总的概率以为是抢N家银行的概率之和… 把状态转移方程写成了f[j]=max{f[j],f[j-q[i].v]+q[i].money}(f[j]表示在概率j之下能抢的大洋);
动态规划DP问题分类和经典题型
u010398493的专栏
10-13 1万+
解题关键： 理解结构特征，抽象出状态，写成状态转移方程。 动态规划理念： 1.最优化原理    1951年美国数学家R．Bellman等人，根据一类多阶段问题的特点，把多阶段决策问题变换为一系列互相联系的单阶段问题，然后逐个加以解决。一些静态模型，只要人为地引进“时间”因素，分成时段，就可以转化成多阶段的动态模型，用动态规划方法去处理。与此同时，他提出了解决这类问题的“
❤️思维导图整理大厂面试高频数组21: 股票问题+冷冻期的两种dp数组定义方式, 力扣309❤️
孤柒的博客
10-24 6142
此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解. 目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容). 关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接. 想进大厂.
思维导图整理大厂面试高频数组22: 股票问题+手续费 和股票II的唯一不同之处, 力扣714
孤柒的博客
10-30 1360
此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解. 目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容). 关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接. 想进大厂.
31.5 一文彻底掌握大厂手撕算法思路 + 答题模板 1.5万行代码+5w字详解 彻底吃透腾讯字节面试知识点 之 手把手教你无情反向拷打面试官
c5dnuser的博客
03-18 699
这是一本写给热爱编程者的“武功秘籍” 本文覆盖树、链表、动态规划、贪心算法等12大主题 总结了常见算法题目的解题思路与实战经验，涵盖链表、树、动态规划、递归回溯等多个核心板块。 以代码为剑，刺破问题的迷雾； 以算法为舟，横渡数据的海洋。​ 适合人群 被LeetCode折磨到脱发的应届毕业生 想转型算法工程师的传统开发老兵 追求极致性能优化的竞赛选手50+可直接套用！！ 本文系统梳理了算法学习的核心模块，涵盖树、链表、动态规划、回溯等12大高频题型，旨在帮助程序员掌握算法本质，建立深度解题思维。文章通过工
思维导图整理大厂面试高频数组23: 股票问题大总结, 彻底搞懂股票问题
孤柒的博客
11-03 1369
此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解. 目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容). 关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接. 想进大厂.
❤️思维导图整理大厂面试高频数组16: 最长湍流子数组的动态规划构建 和 滑动窗口解法, 力扣978❤️
孤柒的博客
10-02 1万+
此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解. 目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容). 关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接. 想进大厂.
❤️思维导图整理大厂面试高频数组19: 股票问题III的dp数组构建/初始化和空间优化难点, 力扣123❤️
孤柒的博客
10-10 1万+
此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解. 目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容). 关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接. 想进大厂.
【AGC005D】~K Perm Counting（计数抽象成图）
2301_77025310的博客
10-01 3663
注意到位置为id，权值为v ,不合法的情况，当且仅当 v = id+k或 v= id-k。dp(i,j,pd)表示考虑到第i号点， 连了j条边，是否有连接i 到 i-1号点。因此，我们把每一个位置和权值抽象成点 ，不合法的情况之间连一条边，可以构成二分图。由此可知，当选了n条边，就恰好n个位置不合法，限制条件是：连的边不能相邻，求出f(m) ，f(m)指代至少有m个位置不合法的方案数。由此总共有2n 个点 k 条链，链与链之间无边 互不干涉。把二分图展开成k条链，进行dp。简单的乘法原理罢了。
Leetcode 68 搜索插入位置 | 寻找比目标字母大的最小字母
im_AMBER的博客
12-04 1065
你的错误逻辑正确逻辑找到 target 时返回 mid-1找到 target 时，继续向右查找（因为需要「大于」target 的最小字符）target <letters [mid] 时，mid 是候选，需保留，right=mid（左闭右开）或不立即排除 mid循环结束直接返回 letters [0]循环结束后，先判断 left 是否越界：越界则返回 letters [0]，否则返回 letters [left]初始right的取值与「越界判断」不匹配；
练题100天——DAY21：统计奇数个数+合并有序数组
2301_81099859的博客
12-07 366
今天写了两道题，难度，并更新了之前的DAY13的冒泡排序+二进制求和、DAY14全排列的思路。
欧几里得距离算法-相似度
weixin_45609702的博客
12-04 216
本文介绍了一个计算欧几里得距离的Java方法。该方法接收两个Double数组作为输入，通过计算对应元素差值的平方和再开方，返回两个数组之间的欧几里得距离值。当输入数组长度不一致时，方法会返回0作为默认值。欧几里得距离算法常用于比较两个数组之间的相似度，是数据分析和机器学习中的基础距离度量方法。
shardingsphere-jdbc分表实现案例和算法比对
Sunchaser的博客
12-08 784
本文档基于shardingsphere-jdbc-core-spring-boot-starter 5.2.1版本验证分表能力，同时基于实际的业务场景对比几类分表策略和实现方案 分库和分表是两个截然不同的功能，分表只要我们在Springboot中引入shardingsphere-jdbc这个依赖库即可，但是分库就要单独部署一个服务shardingsphere-proxy，其他服务连接shardingsphere-proxy，从而实现分库的功能
从零开始写算法——链表篇：相交链表 + 反转链表
最新发布
m0_59624833的博客
12-09 263
leetcode hot100中链表的两个题
C++ ⼀级 2024 年 03 ⽉
weixin_46669997的博客
12-05 50
当 N 为9, 6, 3, 0时，满足条件 N % 3 == 0，因此它们被输出并跟随一个 #。要注意的是，字符串“a+1= ”最后有一个空格，因而输出的内容是：a+1= 2，答案为A。输入21，21%3的结果为0，进入if的分支，因而第4行代码可以被执行。19.【判断题】C++表达式 “10”*2 执行时将报错，因为 “10” 是字符串类型而2是整数类型，它们数据类型不同，不能在一起运算。Cout后面有两个<<，第1个输出字符串5%2=，第2个输出算术运算“5%2”的结果，为1，答案为D。
浅谈：快递物流与算法的相关性（五）
Duoya1105的博客
12-05 184
NP-C 的英文全称是 Non-deterministic Polynomial Complete，即多项式复杂程度的非确定性问题。简单的写法是NP=P？，问题就在这个问号上，到底有没有让NP=P的算法，或是如何证明NP≠P。启发式算法的思想是：在不断解决问题的过程中寻找解决问题的最优方案。再举一个通俗的例子：当我们用数字密码解锁手机时，如果我们不知道密码是多少，必须将所有的数字组合依次尝试。这听起来像是一句废话，如果将它抽象一点的表述，就是：能用电脑快速验证一个解的问题，是否也能够用电脑快速地求出解。
【剑斩OFFER】算法的暴力美学——数青蛙
就业知识博客
12-04 385
力扣1419题：数青蛙
背包九讲：经典动态规划算法详解（原本与修订版）
这是所有背包问题的基础，其核心思想是使用动态规划，定义dp[i][j]表示前i个物品在容量为j时的最大价值，通过状态转移方程dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])实现递推，并可通过滚动数组将空间...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值