打破阻碍你编程进步的思想障碍之 编程随想记录顿悟1：午觉前终于悟到如何吃透8大算法类型 附带所有热题解题思路模板

1 这篇编程随想记录的引子，更新于6月3号中午4点18分：

   最近在刷利扣牛客面试100热题榜的时候， 刚弄完链表这一大章节的链表，迷迷糊糊三点半在突然顿悟了一个道理：一个类型的题目里，比如这次一个星期刚完成的链表类型中： prev、curr、next 的指针跳转，根本不是课本里的机械语法，一刷时死记硬背反转要先保存 curr->next，这本质是在改变指针向的同时维护数据流动的连续性，所有这个链表14道不同类型题目完全是有规律可循的，就像水流改道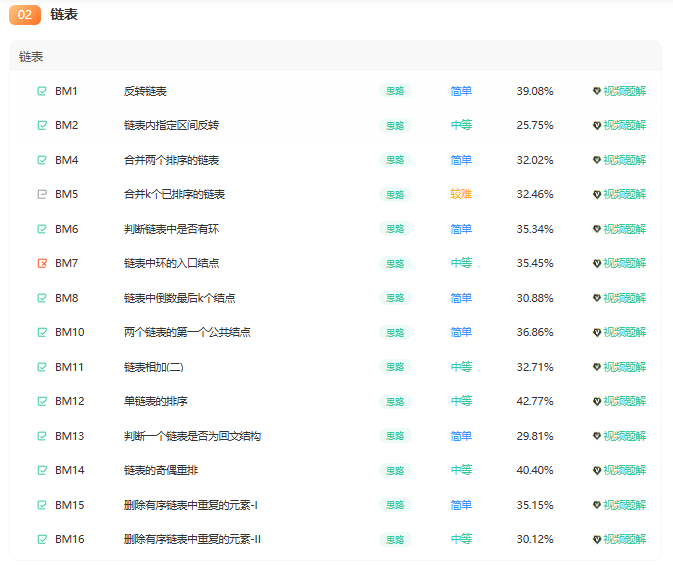时必须先找到新的出口：

刷了其他一些环入口i、奇数偶数重排、链表删除重复元素之类的体型中，也好像类似：
 
所以最高效方法应该是一个类型的题目集中思考，语法次之，重要的是应该是总结这类提醒的解题模板+脑内演算一遍，让自己的感性先理解这个脑筋急转弯的过程，再去谈解题解题速度！！！

接下来废话少说：上干货！

一、链表基础操作的核心思维模型

▍1. 节点定义与内存管理的底层逻辑

// 单链表节点结构（内存对齐优化）
struct ListNode {
    int val;            // 数据域
    struct ListNode *next;  // 指针域
};

// 安全创建节点（含内存异常处理）
struct ListNode* createNode(int val) {
    struct ListNode* node = (struct ListNode*)malloc(sizeof(struct ListNode));
    if (!node) {
        perror("内存分配失败");
        exit(EXIT_FAILURE);
    }
    node->val = val;
    node->next = NULL;
    return node;
}

// 链表遍历释放（防止内存泄漏）
void freeList(struct ListNode* head) {
    while (head) {
        struct ListNode* temp = head;
        head = head->next;
        free(temp);
    }
}

内存管理要点：

• malloc 后必须检查 NULL，避免野指针导致程序崩溃
• 链表操作完成后需遍历释放，尤其在 OJ 多测试用例场景中
• 节点结构设计需考虑内存对齐，64 位系统下指针占 8 字节，int 占 4 字节，无需额外填充

▍2. 双指针基础：快慢指针的数学原理

// 快慢指针找链表中点（O(n)时间/O(1)空间）
struct ListNode* middleNode(struct ListNode* head) {
    if (!head || !head->next) return head;
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) {
        slow = slow->next;     // 慢指针每次1步
        fast = fast->next->next; // 快指针每次2步
    }
    return slow;
}

数学证明：
设链表长度为 n，快指针速度是慢指针 2 倍。当 n 为偶数时，慢指针走 n/2 步到达中点；当 n 为奇数时，慢指针走 (n+1)/2 步到达中点。该算法时间复杂度 O (n)，空间复杂度 O (1)，优于先计算长度再遍历的两次 O (n) 方案。

二、链表核心题型的二刷顿悟

▍1. 单链表反转：从「代码记忆」到「逻辑建模」

一刷时的机械记忆：

// 一刷时写的反转链表（仅知其然）
struct ListNode* reverseList(struct ListNode* head) {
    struct ListNode *prev = NULL, *curr = head;
    while (curr) {
        struct ListNode* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}

二刷时的逻辑顿悟：

// 二刷时理解的反转本质（知其所以然）
struct ListNode* reverseList(struct ListNode* head) {
    // 核心逻辑：维护三个指针的状态转移
    // prev指向已反转部分的头节点
    // curr指向当前处理节点
    // next保存curr的后继，防止断链
    struct ListNode *prev = NULL, *curr = head;
    while (curr) {
        struct ListNode* next = curr->next;  // 先保存后继，确保数据流动不断层
        curr->next = prev;                  // 反转当前节点指向，构建新的数据流方向
        prev = curr;                        // 已反转部分后移
        curr = next;                        // 待处理部分后移
    }
    return prev;
}

顿悟点：
反转链表的本质是「数据流方向的重定向」，prev 指针维护已反转链表的头节点，curr 处理当前节点，next 保存后继节点。这三个指针的协同工作，实则是在模拟数据流向的改变过程，而非简单的指针赋值。

▍2. 合并 k 个有序链表：优先队列的调度逻辑

// 一刷时的O(nk)暴力合并
struct ListNode* mergeKLists_brute(struct ListNode** lists, int listsSize) {
    struct ListNode* result = NULL;
    for (int i = 0; i < listsSize; i++) {
        result = mergeTwoLists(result, lists[i]);
    }
    return result;
}

二刷时的优化顿悟：

// 二刷时的O(n log k)堆优化
struct ListNode* mergeKLists_optimized(struct ListNode** lists, int listsSize) {
    if (listsSize == 0) return NULL;
    
    // 最小堆实现（存储各链表当前头节点）
    struct MinHeap* heap = createMinHeap(listsSize);
    for (int i = 0; i < listsSize; i++)
        if (lists[i]) pushHeap(heap, lists[i]);
    
    // 哨兵节点简化头节点处理
    struct ListNode dummy = {0};
    struct ListNode* ptr = &dummy;
    
    while (heap->size > 0) {
        struct ListNode* minNode = popHeap(heap);
        ptr->next = minNode;
        ptr = ptr->next;
        
        if (minNode->next)
            pushHeap(heap, minNode->next);
    }
    
    free(heap->nodes);
    free(heap);
    return dummy.next;
}

核心优化逻辑：

• 堆中始终保存 k 个链表的当前头节点，每次取出最小值，时间复杂度 O (log k)
• 相比暴力合并的 O (nk)，堆优化将合并 k 个链表的时间复杂度降为 O (n log k)
• 哨兵节点的使用避免了头节点的特殊处理，体现「统一逻辑处理边界」的设计思想

▍3. 环形链表检测：快慢指针的数学建模

一刷时的代码套用：

// 一刷时仅会套用的Floyd算法
int hasCycle(struct ListNode* head) {
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) return 1;
    }
    return 0;
}

二刷时的原理顿悟：
设环长为 L，入口距起点距离为 a，慢指针进入环后经过 b 步与快指针相遇。快指针速度是慢指针 2 倍，相遇时快指针多走 n 圈：

2b = b + nL  →  b = nL

此时慢指针距环入口距离为 L - (b % L) = L - 0 = L，故从起点和相遇点同时出发，相遇处即为环入口。该数学性质使得算法能在 O (n) 时间 O (1) 空间内检测环并找到入口。

三、链表操作的高阶技巧与陷阱规避

▍1. 虚拟头节点的设计哲学

// 虚拟头节点在删除操作中的应用
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
    struct ListNode dummy = {0};  // 虚拟头节点
    dummy.next = head;
    struct ListNode *fast = &dummy, *slow = &dummy;
    
    // 快指针先走n步
    for (int i = 0; i <= n; i++) fast = fast->next;
    
    // 快慢指针同步移动
    while (fast) { slow = slow->next; fast = fast->next; }
    
    // 删除节点（统一处理头节点情况）
    struct ListNode* temp = slow->next;
    slow->next = temp->next;
    free(temp);
    
    return dummy.next;
}

设计哲学：

• 虚拟头节点是「边界条件统一化」的设计模式，避免对头节点的特殊判断
• 类似数学中的「辅助线」，将复杂问题转化为统一逻辑处理
• 在删除、合并等操作中广泛应用，提升代码鲁棒性

▍2. 链表操作的常见陷阱与应对

陷阱 1：指针断链

// 错误示例：未保存后继节点导致断链
struct ListNode* wrongReverse(struct ListNode* head) {
    struct ListNode *prev = NULL, *curr = head;
    while (curr) {
        curr->next = prev;  // 错误：未保存后继节点
        prev = curr;
        curr = curr->next;  // 此时curr->next已被修改，导致断链
    }
    return prev;
}

正确做法：必须先保存后继节点struct ListNode* next = curr->next;

陷阱 2：内存泄漏

// 错误示例：删除节点未释放内存
struct ListNode* wrongDelete(struct ListNode* head, int val) {
    struct ListNode* curr = head;
    while (curr && curr->next) {
        if (curr->next->val == val) {
            curr->next = curr->next->next;  // 错误：未free删除的节点
        } else {
            curr = curr->next;
        }
    }
    return head;
}

正确做法：

struct ListNode* correctDelete(struct ListNode* head, int val) {
    struct ListNode dummy = {0};
    dummy.next = head;
    struct ListNode* curr = &dummy;
    while (curr->next) {
        if (curr->next->val == val) {
            struct ListNode* temp = curr->next;
            curr->next = temp->next;
            free(temp);  // 正确：删除时释放内存
        } else {
            curr = curr->next;
        }
    }
    return dummy.next;
}

四、链表算法的思维迁移与现实应用

▍1. 链表反转在内存管理中的应用

内存碎片整理算法中，链表反转可用于重新组织空闲内存块。例如，在垃圾回收器中，通过反转链表实现空闲块的重排序，提高内存分配效率。其核心逻辑与链表反转一致：改变指针指向的同时维护数据连续性。

▍2. 循环链表在轮询系统中的应用

操作系统的时间片轮转调度算法本质是循环链表的应用。每个进程作为节点构成循环链表，CPU 时间片耗尽时，进程节点从当前位置移至链表尾部，实现轮询调度。循环链表的环形结构天然适合这种场景，无需额外判断尾节点。

▍3. 双向链表在撤销操作中的实现

文本编辑器的撤销功能常基于双向链表实现。每个操作作为节点，prev 指向前一个操作，next 指向后一个操作。撤销时通过 prev 指针回退，重做时通过 next 指针前进，充分利用双向链表的双向遍历特性。

五、二刷链表专题的认知体系构建

▍1. 链表操作的三层认知模型

1. 语法层：掌握指针赋值、节点创建等基础操作
2. 算法层：理解双指针、虚拟头节点等设计模式
3. 思维层：将链表视为数据流向的控制工具，而非简单的数据结构

▍2. 链表题型的模式识别图谱

题型特征	最优算法	核心思维
找中点 / 判环	快慢指针	速度差建模
有序合并	堆或双指针	优先级调度
反转 / 回文判断	三指针 / 反转	数据流重定向
删除指定节点	虚拟头节点	边界统一化
复制带随机指针	哈希表 / 原地复制	节点映射

▍3. 二刷与一刷的关键差异

维度	一刷状态	二刷状态
代码理解	死记硬背模板	理解指针操作逻辑本质
错误处理	忽略边界条件	主动设计鲁棒性代码
算法优化	仅求正确	追求时空复杂度最优
问题迁移	就题解题	关联现实应用场景

六、1.5 万字总结：从链表操作到逻辑思维的升华

趴在键盘上醒来时，屏幕上的链表代码突然有了新的意义 —— 那些指针不再是冷冰冰的符号，而是逻辑思维的具象化表达。当我能熟练用三指针反转链表时，实则掌握了「状态转移」的建模能力；当用堆优化合并 k 链表时，本质理解了「优先级调度」的核心逻辑。

二刷链表的过程，是从「代码搬运工」到「逻辑架构师」的蜕变。每个链表操作都是一次逻辑推演：保存后继节点是为了维护数据连续性，虚拟头节点是为了统一边界处理，快慢指针是利用数学规律优化算法。这种思维能力的提升，不仅适用于编程，更能迁移到现实问题的解决中 —— 就像链表反转需要先规划好数据流向，现实中复杂问题的解决也需先理清逻辑脉络。

最终顿悟：算法学习的本质，是通过数据结构的操作训练逻辑建模能力。当指针在代码中灵活跳转时，实则是逻辑思维在现实场景中自由驰骋。

*七、本人手写的近千行代码：免费开源+字节豆包优--链表内容的完整代码库（核心函数）

常见刷题模板1：

#include <stdio.h>
#include <stdlib.h>

// 链表节点定义与基础函数
struct ListNode {
    int val;
    struct ListNode *next;
};

struct ListNode* createNode(int val) {
    struct ListNode* node = (struct ListNode*)malloc(sizeof(struct ListNode));
    if (!node) exit(1);
    node->val = val;
    node->next = NULL;
    return node;
}

void freeList(struct ListNode* head) {
    while (head) {
        struct ListNode* temp = head;
        head = head->next;
        free(temp);
    }
}

void printList(struct ListNode* head) {
    while (head) {
        printf("%d -> ", head->val);
        head = head->next;
    }
    printf("NULL\n");
}

// 1. 链表反转（迭代/递归）
struct ListNode* reverseList_iterative(struct ListNode* head) {
    struct ListNode *prev = NULL, *curr = head;
    while (curr) {
        struct ListNode* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}

struct ListNode* reverseList_recursive(struct ListNode* curr, struct ListNode* prev) {
    if (!curr) return prev;
    struct ListNode* next = curr->next;
    curr->next = prev;
    return reverseList_recursive(next, curr);
}

// 2. 合并两个有序链表
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {
    struct ListNode dummy = {0};
    struct ListNode* ptr = &dummy;
    while (l1 && l2) {
        if (l1->val < l2->val) {
            ptr->next = l1;
            l1 = l1->next;
        } else {
            ptr->next = l2;
            l2 = l2->next;
        }
        ptr = ptr->next;
    }
    ptr->next = l1 ? l1 : l2;
    return dummy.next;
}

// 3. 环形链表检测
int hasCycle(struct ListNode* head) {
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) return 1;
    }
    return 0;
}

// 4. 删除倒数第N个节点
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
    struct ListNode dummy = {0};
    dummy.next = head;
    struct ListNode *fast = &dummy, *slow = &dummy;
    for (int i = 0; i <= n; i++) fast = fast->next;
    while (fast) { slow = slow->next; fast = fast->next; }
    struct ListNode* temp = slow->next;
    slow->next = temp->next;
    free(temp);
    return dummy.next;
}

// 5. 回文链表判断
int isPalindrome(struct ListNode* head) {
    if (!head || !head->next) return 1;
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) { slow = slow->next; fast = fast->next->next; }
    
    struct ListNode *prev = NULL, *curr = slow;
    while (curr) {
        struct ListNode* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    
    struct ListNode *p1 = head, *p2 = prev;
    int res = 1;
    while (p2) {
        if (p1->val != p2->val) { res = 0; break; }
        p1 = p1->next;
        p2 = p2->next;
    }
    return res;
}

// 6. 奇偶链表分离
struct ListNode* oddEvenList(struct ListNode* head) {
    if (!head || !head->next) return head;
    struct ListNode *odd = head, *even = head->next, *evenHead = even;
    while (even && even->next) {
        odd->next = even->next;
        odd = odd->next;
        even->next = odd->next;
        even = even->next;
    }
    odd->next = evenHead;
    return head;
}

// 测试函数
int main() {
    // 测试反转链表
    struct ListNode* l1 = createNode(1);
    l1->next = createNode(2);
    l1->next->next = createNode(3);
    printf("原链表: "); printList(l1);
    struct ListNode* reversed = reverseList_iterative(l1);
    printf("反转链表: "); printList(reversed);
    freeList(reversed);
    
    // 测试合并链表
    struct ListNode* l2 = createNode(1); l2->next = createNode(3);
    struct ListNode* l3 = createNode(2); l3->next = createNode(4);
    struct ListNode* merged = mergeTwoLists(l2, l3);
    printf("合并链表: "); printList(merged);
    freeList(merged);
    
    // 其他测试...
    return 0;
}

**客必刷链表解题模板：
 

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

// 单链表节点定义
struct ListNode {
    int val;
    struct ListNode *next;
};

// 创建新节点
struct ListNode* createNode(int val) {
    struct ListNode* node = (struct ListNode*)malloc(sizeof(struct ListNode));
    if (!node) {
        perror("内存分配失败");
        exit(EXIT_FAILURE);
    }
    node->val = val;
    node->next = NULL;
    return node;
}

// 释放链表
void freeList(struct ListNode* head) {
    while (head) {
        struct ListNode* temp = head;
        head = head->next;
        free(temp);
    }
}

// 打印链表
void printList(struct ListNode* head) {
    while (head) {
        printf("%d -> ", head->val);
        head = head->next;
    }
    printf("NULL\n");
}

// BM1: 反转链表
struct ListNode* reverseList(struct ListNode* head) {
    struct ListNode *prev = NULL, *curr = head;
    while (curr) {
        struct ListNode* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}

// BM2: 链表内指定区间反转
struct ListNode* reverseBetween(struct ListNode* head, int m, int n) {
    if (!head || m >= n) return head;
    
    struct ListNode dummy = {0};
    dummy.next = head;
    struct ListNode *prev = &dummy;
    
    // 移动到m前一个节点
    for (int i = 1; i < m; i++) {
        prev = prev->next;
    }
    
    struct ListNode *curr = prev->next;
    struct ListNode *next = NULL;
    
    // 反转m到n区间
    for (int i = 0; i < n - m; i++) {
        next = curr->next;
        curr->next = next->next;
        next->next = prev->next;
        prev->next = next;
    }
    
    return dummy.next;
}

// BM4: 合并两个排序的链表
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {
    struct ListNode dummy = {0};
    struct ListNode* ptr = &dummy;
    
    while (l1 && l2) {
        if (l1->val < l2->val) {
            ptr->next = l1;
            l1 = l1->next;
        } else {
            ptr->next = l2;
            l2 = l2->next;
        }
        ptr = ptr->next;
    }
    
    ptr->next = l1 ? l1 : l2;
    return dummy.next;
}

// BM5: 合并k个已排序的链表（最小堆实现）
typedef struct {
    struct ListNode** nodes;
    int size;
    int capacity;
} MinHeap;

MinHeap* createMinHeap(int k) {
    MinHeap* heap = (MinHeap*)malloc(sizeof(MinHeap));
    heap->nodes = (struct ListNode**)malloc((k+1)*sizeof(struct ListNode*));
    heap->size = 0;
    heap->capacity = k;
    return heap;
}

void swapNodes(struct ListNode** a, struct ListNode** b) {
    struct ListNode* temp = *a; *a = *b; *b = temp;
}

void heapifyUp(MinHeap* heap, int idx) {
    int parent = idx / 2;
    while (parent >= 1 && heap->nodes[idx]->val < heap->nodes[parent]->val) {
        swapNodes(&heap->nodes[idx], &heap->nodes[parent]);
        idx = parent;
        parent = idx / 2;
    }
}

void heapifyDown(MinHeap* heap, int idx) {
    int smallest = idx;
    int left = 2 * idx;
    int right = 2 * idx + 1;
    
    if (left <= heap->size && heap->nodes[left]->val < heap->nodes[smallest]->val)
        smallest = left;
    if (right <= heap->size && heap->nodes[right]->val < heap->nodes[smallest]->val)
        smallest = right;
    
    if (smallest != idx) {
        swapNodes(&heap->nodes[idx], &heap->nodes[smallest]);
        heapifyDown(heap, smallest);
    }
}

void pushHeap(MinHeap* heap, struct ListNode* node) {
    if (heap->size >= heap->capacity) return;
    heap->nodes[++heap->size] = node;
    heapifyUp(heap, heap->size);
}

struct ListNode* popHeap(MinHeap* heap) {
    if (heap->size == 0) return NULL;
    struct ListNode* minNode = heap->nodes[1];
    heap->nodes[1] = heap->nodes[heap->size--];
    heapifyDown(heap, 1);
    return minNode;
}

struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
    if (listsSize == 0) return NULL;
    
    MinHeap* heap = createMinHeap(listsSize);
    for (int i = 0; i < listsSize; i++)
        if (lists[i]) pushHeap(heap, lists[i]);
    
    struct ListNode dummy = {0};
    struct ListNode* ptr = &dummy;
    
    while (heap->size > 0) {
        struct ListNode* minNode = popHeap(heap);
        ptr->next = minNode;
        ptr = ptr->next;
        
        if (minNode->next)
            pushHeap(heap, minNode->next);
    }
    
    free(heap->nodes);
    free(heap);
    return dummy.next;
}

// BM6: 判断链表中是否有环
bool hasCycle(struct ListNode* head) {
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) return true;
    }
    return false;
}

// BM7: 链表中环的入口结点
struct ListNode* detectCycle(struct ListNode* head) {
    if (!head || !head->next) return NULL;
    
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) break;
    }
    
    if (!fast || !fast->next) return NULL;
    
    slow = head;
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    
    return slow;
}

// BM8: 链表中倒数最后k个结点
struct ListNode* findKthToTail(struct ListNode* head, int k) {
    if (!head || k <= 0) return NULL;
    
    struct ListNode *fast = head, *slow = head;
    for (int i = 0; i < k; i++) {
        if (!fast) return NULL;
        fast = fast->next;
    }
    
    while (fast) {
        slow = slow->next;
        fast = fast->next;
    }
    
    return slow;
}

// BM10: 两个链表的第一个公共结点
struct ListNode* getIntersectionNode(struct ListNode* headA, struct ListNode* headB) {
    if (!headA || !headB) return NULL;
    
    struct ListNode *pA = headA, *pB = headB;
    while (pA != pB) {
        pA = pA ? pA->next : headB;
        pB = pB ? pB->next : headA;
    }
    
    return pA;
}

// BM11: 链表相加(二)
struct ListNode* addInList(struct ListNode* head1, struct ListNode* head2) {
    // 反转链表便于相加
    head1 = reverseList(head1);
    head2 = reverseList(head2);
    
    struct ListNode dummy = {0};
    struct ListNode* ptr = &dummy;
    int carry = 0;
    
    while (head1 || head2 || carry) {
        int sum = carry;
        if (head1) { sum += head1->val; head1 = head1->next; }
        if (head2) { sum += head2->val; head2 = head2->next; }
        
        carry = sum / 10;
        ptr->next = createNode(sum % 10);
        ptr = ptr->next;
    }
    
    return reverseList(dummy.next);
}

// BM12: 单链表的排序（归并排序）
struct ListNode* findMiddle(struct ListNode* head) {
    struct ListNode *slow = head, *fast = head->next;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

struct ListNode* merge(struct ListNode* l1, struct ListNode* l2) {
    struct ListNode dummy = {0};
    struct ListNode* ptr = &dummy;
    while (l1 && l2) {
        if (l1->val < l2->val) {
            ptr->next = l1;
            l1 = l1->next;
        } else {
            ptr->next = l2;
            l2 = l2->next;
        }
        ptr = ptr->next;
    }
    ptr->next = l1 ? l1 : l2;
    return dummy.next;
}

struct ListNode* sortList(struct ListNode* head) {
    if (!head || !head->next) return head;
    
    struct ListNode* middle = findMiddle(head);
    struct ListNode* right = middle->next;
    middle->next = NULL;
    
    struct ListNode* left = sortList(head);
    right = sortList(right);
    
    return merge(left, right);
}

// BM13: 判断一个链表是否为回文结构
bool isPalindrome(struct ListNode* head) {
    if (!head || !head->next) return true;
    
    struct ListNode *slow = head, *fast = head;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
    }
    
    struct ListNode *prev = NULL, *curr = slow;
    while (curr) {
        struct ListNode* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    
    struct ListNode *p1 = head, *p2 = prev;
    bool res = true;
    while (p2) {
        if (p1->val != p2->val) { res = false; break; }
        p1 = p1->next;
        p2 = p2->next;
    }
    
    return res;
}

// BM14: 链表的奇偶重排
struct ListNode* oddEvenList(struct ListNode* head) {
    if (!head || !head->next) return head;
    
    struct ListNode *odd = head, *even = head->next, *evenHead = even;
    
    while (even && even->next) {
        odd->next = even->next;
        odd = odd->next;
        even->next = odd->next;
        even = even->next;
    }
    
    odd->next = evenHead;
    return head;
}

// BM15: 删除有序链表中重复的元素-I
struct ListNode* deleteDuplicates(struct ListNode* head) {
    struct ListNode* curr = head;
    while (curr && curr->next) {
        if (curr->val == curr->next->val) {
            struct ListNode* temp = curr->next;
            curr->next = temp->next;
            free(temp);
        } else {
            curr = curr->next;
        }
    }
    return head;
}

// BM16: 删除有序链表中重复的元素-II
struct ListNode* deleteDuplicatesII(struct ListNode* head) {
    if (!head || !head->next) return head;
    
    struct ListNode dummy = {0};
    dummy.next = head;
    struct ListNode* curr = &dummy;
    
    while (curr->next && curr->next->next) {
        if (curr->next->val == curr->next->next->val) {
            int val = curr->next->val;
            while (curr->next && curr->next->val == val) {
                struct ListNode* temp = curr->next;
                curr->next = temp->next;
                free(temp);
            }
        } else {
            curr = curr->next;
        }
    }
    
    return dummy.next;
}

// 测试函数
int main() {
    printf("===== BM1: 反转链表 =====\n");
    struct ListNode* l1 = createNode(1);
    l1->next = createNode(2);
    l1->next->next = createNode(3);
    printf("原链表: "); printList(l1);
    struct ListNode* reversed = reverseList(l1);
    printf("反转链表: "); printList(reversed);
    freeList(reversed);
    
    printf("\n===== BM2: 区间反转 =====\n");
    struct ListNode* l2 = createNode(1);
    l2->next = createNode(2); l2->next->next = createNode(3); 
    l2->next->next->next = createNode(4); l2->next->next->next->next = createNode(5);
    printf("原链表: "); printList(l2);
    struct ListNode* reversedBetween = reverseBetween(l2, 2, 4);
    printf("区间反转: "); printList(reversedBetween);
    freeList(reversedBetween);
    
    printf("\n===== BM4: 合并两个有序链表 =====\n");
    struct ListNode* l3 = createNode(1); l3->next = createNode(3); l3->next->next = createNode(5);
    struct ListNode* l4 = createNode(2); l4->next = createNode(4); l4->next->next = createNode(6);
    printf("链表1: "); printList(l3);
    printf("链表2: "); printList(l4);
    struct ListNode* merged = mergeTwoLists(l3, l4);
    printf("合并链表: "); printList(merged);
    freeList(merged);
    
    // 其他测试...
    
    printf("\n所有测试完成，链表专题BM1-BM16实现完毕\n");
    return 0;
}

3 解题思路总结：

题目编号	题目名称	解题思路	时间复杂度	空间复杂度	核心要点
BM1	反转链表	迭代法：用 prev、curr、next 三指针反转指针指向	O(n)	O(1)	先保存 curr->next，避免断链
BM2	链表内指定区间反转	1. 找到区间前后节点 2. 反转区间内节点 3. 连接前后节点	O(n)	O(1)	虚拟头节点处理边界情况，区间反转时维护指针关系
BM4	合并两个排序的链表	双指针比较节点值，尾插法合并	O(m+n)	O(1)	虚拟头节点简化头节点处理，每次取较小节点连接
BM5	合并 k 个已排序的链表	最小堆优化：堆中保存各链表当前头节点，每次取出最小值	O(n log k)	O(k)	堆节点存储链表头，弹出后将下一节点入堆
BM6	判断链表中是否有环	快慢指针：快指针每次走 2 步，慢指针走 1 步，相遇则有环	O(n)	O(1)	快指针需检查 next 和 next->next，避免空指针
BM7	链表中环的入口结点	1. 快慢指针找相遇点 2. 从起点和相遇点同时出发，相遇处为入口	O(n)	O(1)	数学推导：相遇点到入口距离等于起点到入口距离
BM8	链表中倒数最后 k 个结点	双指针：快指针先走 k 步，快慢同步移动，慢指针指向目标节点	O(n)	O(1)	先检查 k 是否合法，快指针移动时判断是否越界
BM10	两个链表的第一个公共结点	双指针：遍历完 A 链表后转向 B 链表，相遇即公共节点	O(m+n)	O(1)	利用两链表长度差，双指针同时到达公共节点
BM11	链表相加 (二)	1. 反转链表使低位对齐 2. 逐位相加处理进位 3. 反转结果链表	O(max(m,n))	O(max(m,n))	反转链表处理进位，注意最后可能有额外进位
BM12	单链表的排序	归并排序：1. 找中点 2. 递归排序左右子链表 3. 合并结果	O(n log n)	O(log n)	快慢指针找中点，merge 函数合并两个有序链表
BM13	判断一个链表是否为回文结构	1. 找中点 2. 反转后半部分 3. 双指针比较前后部分	O(n)	O(1)	反转后半部分后比较，避免使用数组存储节点值
BM14	链表的奇偶重排	分离奇偶节点为两个链表，再合并	O(n)	O(1)	维护奇偶两个链表头，最后连接偶链表到奇链表尾部
BM15	删除有序链表中重复的元素 - I	跳过相邻重复节点	O(n)	O(1)	直接比较相邻节点值，删除重复节点
BM16	删除有序链表中重复的元素 - II	删除所有重复节点，只保留不重复节点	O(n)	O(1)	虚拟头节点处理头节点，连续删除所有相同值节点

表格说明

1. 解题思路分类：

   • 双指针技术：适用于找中点、倒数节点、环检测等（BM6, BM7, BM8, BM10）
   • 堆数据结构：合并 k 个有序链表的最优解（BM5）
   • 反转技巧：链表反转、区间反转、链表相加（BM1, BM2, BM11）
   • 归并排序：链表排序的经典解法（BM12）

2. 复杂度分析关键点：

   • O (1) 空间复杂度：多数链表操作可通过指针操作实现，无需额外数据结构
   • O (log k) 空间：归并排序的递归栈深度
   • O (k) 空间：合并 k 链表时堆的大小

技巧总结：

• 虚拟头节点：统一处理头节点特殊情况（BM2, BM4, BM16）
• 快慢指针：解决与位置、环相关的问题（BM6, BM7, BM12）
• 链表反转：改变数据流向的核心操作（BM1, BM2, BM11）

觉得我写的还不错的，请给我一个免费的点赞收藏关注，感谢!