年初的c语言教程深度底层原理、指针深探系列大获好评点赞收藏之后,本人在秋招和春招季又写了一个这个大家一直在让我写、但是但是之前一直没空的手写一百道力扣牛客面试必刷热题教程。今年四月份清明节之后有空了,就在本地vs code帮大家写了一这个手写牛客面试必刷一百题,也算是完成了打击给我的任务吧23333
1 算法之美
本人呕心沥血花了一个多月在2025春季,亲自总结了一百道力扣和牛客热题包括各大厂面试必考和算法数据结构的思维总结,共享出来给大家,一是督促自己多分享算法知识和数据结构的练习方法二是也为自己的学习增加一份动力分享与是最好的学习动力这话不是开玩笑的。此帖包含两万多行本地vs code代码和六万字的详细总结,不是其他的把csdn当成自媒体炒作的博主可以碰瓷的23333
1 本神贴在此验证代码之美!编程——工程师的思考录
1 算法,是每个程序员必须征服的星辰大海。本人此贴力求:涵盖树、链表、动态规划、回溯等12大核心模块无论你是苦于大厂笔试的应届生,还是渴望突破技术瓶颈的工作人士!
之前4月的同步牛客进度:
未来的任务分类:
1 链表、查找、树、栈队列、 哈希
2 递归、回溯、贪心
3 字符串、双指针、模拟
其实只有三类!
2 三重境界-目前笔者在1-2
初学算法时,眼中只有输入输出,却看不懂背后的思维。直到反复实践后,才逐渐领悟到“见题不是题”的奥义:
-
第一境:暴力美学
面对二叉树遍历,曾执着于写满递归终止条件;遇到动态规划,用备忘录硬怼所有状态。 -
第二境:模式识别
-
236的二叉树的最近公共祖先与剑指Offer 68. 二叉搜索树最近公共祖先实为同源问题时,顿悟算法本质是抽象!
-
第三境:回头那人却在灯火阑珊处
在解决329. 矩阵中的最长递增路径时,记忆化搜索(Memoization)与拓扑排序的融合让我意识到:高阶算法不是套模板,而是灵活运用这个场景的合适思维模式
所以初学者应该掌握基础数据结构(数组、链表、栈、队列、哈希表、堆、树、图、Trie、并查集)
策略:每日精做3题,使用五遍法(当天→3天后→1周后→1月后→面试前)
6大算法范式(分治、贪心、回溯、动态规划、图论、位运算)
策略:建立错题本,标注思维断点 如:为何此处想不到状态压缩
当然了,小于150的勿扰!!!!
完整代码与思维导图已整理至博客园、csdn、GitHub仓库,关注后在csdn或者力扣私信我获取。
2 各类题目总结:本人亲自在vscode上本地运行环境带写!
2.1 树
1.找对最近的公共祖先:
int func(struct TreeNode* root,int o1,int o2){
int lowestCommonAncestor(struct TreeNode* root, int o1, int o2 ) {
// write code here
if(root==NULL){
return -1;
}
if( root->val==o1 ||root->val==o2){
return root->val;
}
int lres = lowestCommonAncestor(root->left, o1, o2);
int rres = lowestCommonAncestor(root->right, o1, o2);
if(lres == -1) return rres;
if(rres == -1) return lres;
return root->val;
}
}
2.树的遍历
思路:直接递归
太简单,跳过!!!
3.合并树
struct TreeNode* mergeTrees(struct TreeNode* t1, struct TreeNode* t2 ) {
// write code here
if(t1==NULL ){
return t2;
}
if(t2 == NULL){
return t1;
}
if(t1==NULL && t2==NULL){
return t1;
}
t1->val+= t2->val;
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right,t2->right);
return t1;
}
4. 镜像树
struct TreeNode* Mirror(struct TreeNode* pRoot ) {
// write code here
if(pRoot==NULL){
return pRoot;
}
struct TreeNode* temp;
temp = pRoot->left;
pRoot->left = pRoot->right ;
pRoot->right = temp ;
Mirror(pRoot->left);
Mirror(pRoot->right);
return pRoot;
}
5 是否是二叉搜索树?
void doFunc(struct TreeNode* n, int* list, int* listSize) {
if (!n) {
return ;
}
doFunc(n->left, list, listSize);
list[(*listSize)++] = n->val;
doFunc(n->right, list, listSize);
}
bool isValidBST(struct TreeNode* root ) {
int* list = (int* )malloc(1000000*sizeof(int));
int listSize = 0 ;
doFunc(root,list,&listSize);
// int res =
for( int i=0;i<listSize-1;i++ ){
if(list[i]>list[i+1] ){
return false;
}
}
return true;
}
6 完全二叉树?
只要发现front前面这个节点是空的,如果在发现空的,那就一定有错误--

bool isCompleteTree(struct TreeNode* root ) {
// write code here
int rear=0,front=0;
struct TreeNode* list[10000];
list[rear++] = root;
while(front<rear){
struct TreeNode* cur = list[front++];
if(cur==NULL){
while(front<rear){
if(list[front]!=NULL){
return 0;
}
front++;
}
}
else{
list[rear++] = cur->left;
list[rear++] = cur->right;
}
}
return 1;
}
7 平衡二叉树?
看每个节点最大差值《=1???
1 - 找到每一个节点,返回来,在递归 2 - 在里面再来一次两次判断,看看两边的子树是不是都满足?
int getLen(struct TreeNode* root) {
if (root == NULL) {
return 0 ;
}
int lLen = getLen(root->left);
int rLen = getLen(root->right);
return (lLen>rLen?lLen:rLen)+1;
}
bool IsBalanced_Solution(struct TreeNode* pRoot ) {
// write code here
if(pRoot==NULL){
return 1;
}
int lLen = getLen(pRoot->left);
int rLen = getLen(pRoot->right);
if(abs(lLen-rLen)>1){
return 0;
}
return IsBalanced_Solution(pRoot->left)&&IsBalanced_Solution(pRoot->right);
}
8 二叉搜索树的最近的祖先节点???
直接秒杀!!!!
int lowestCommonAncestor(struct TreeNode* root, int p, int q ) {
// write code here
if(root->val==p || root->val==q){
return root->val;
}
if( (root->val<p && root->val<q) ){
return lowestCommonAncestor(root->right, p, q);
}
if( root->val>p && root->val>q ){
return lowestCommonAncestor(root->left, p, q);
}
if(( root->val<p &&root->val>q ) || (root->val<q &&root->val>p )){
return root->val;
}
else{
return -1;
}
}
9.树的最近公共祖先????
分析:对于x要么是a,要么是b,要么都是x的子树的节点!!!
思路:递归+特殊情况处理
int lowestCommonAncestor(struct TreeNode* root, int o1, int o2 ) {
// write code here
// if(root==NULL){
// return -1;
// }
// if( root->val==o1 ||root->val==o2){
// return root->val;
// }
// int lres = lowestCommonAncestor(root->left, o1, o2);
// int rres = lowestCommonAncestor(root->right, o1, o2);
// if(lres == -1) return rres;
// if(rres == -1) return lres;
// return root->val;
if(root==NULL){
return -1;
}
if(root->val==o1 || root->val==o2){
return root->val;
}
int lres = lowestCommonAncestor(root->left, o1, o2);
int rres = lowestCommonAncestor(root->right, o1, o2);
if(lres==-1) return rres;
if(rres==-1) return lres;
return root->val;
}
10.重建二叉树:从pre+in遍历重新构建一个二叉树
分析:_f_ _____pre ____ ____in_____
_____pre_____ _f_ _____in______
只要看到这个,就明白!
11.右视图
2.2 链表
3/16号全部刷完:

1.反转链表
pre/p/pNext 三大元基本法!!!不用想,直接套模板!!!
2.第一个公共节点?
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
/**
*
* @param pHead1 ListNode类
* @param pHead2 ListNode类
* @return ListNode类
*/
struct ListNode* FindFirstCommonNode(struct ListNode* pHead1,
struct ListNode* pHead2 ) {
// write code here
// struct ListNode* p = pHead1;
// struct ListNode* q = pHead2;
// if(pHead1==NULL || pHead2 ==NULL){
// return NULL;
// }
// while( p->val!=q->val ) {
// p=p->next;
// q=q->next;
// if(p==NULL && q == NULL){
// return NULL;
// }
// if(p==NULL){
// p= pHead2;
// }
// if(q==NULL){
// q = pHead1;
// }
// }
// return p;
// if (pHead1 == NULL || pHead2 == NULL) {
// return NULL;
// }
// struct ListNode* p1 = pHead1;
// struct ListNode* p2 = pHead2;
// while (p1 != p2) {
// p1 = p1->next;
// p2 = p2->next;
// if(p1==NULL&&p2==NULL){
// return NULL;
// }
// if (p1 == NULL) {
// p1 = pHead2;
// }
// if (p2 == NULL) {
// p2 = pHead1;
// }
// }
// return p1;
if (pHead1 == NULL || pHead2 == NULL) {
return NULL; // 如果任一链表为空,直接返回 NULL
}
struct ListNode* p1 = pHead1;
struct ListNode* p2 = pHead2;
// 双指针遍历
while(p1!=p2){
p1 = p1==NULL?pHead2:p1->next;
p2 = p2==NULL?pHead1:p2->next;
}
return p1; // 返回公共节点(如果没有公共节点,返回 NULL)
}
3.合并两个排序链表
太简单了,指针谁小谁做下一个,不放图了
4 两个链表相加的
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head1 ListNode类
* @param head2 ListNode类
* @return ListNode类
*/
struct ListNode* doFunc(struct ListNode* node){
struct ListNode* p=node;
struct ListNode* pre=NULL ;
struct ListNode* pNext ;
while(p!=NULL){
pNext = p->next;
p->next = pre;
pre = p ;
p = pNext;
}
return pre;
}
struct ListNode* addInList(struct ListNode* head1, struct ListNode* head2 ) {
// write code here
struct ListNode* a = doFunc(head1);
struct ListNode* b = doFunc(head2);
struct ListNode* s = NULL;
struct ListNode* head= s;
int jin = 0 ;
while(a!=NULL || b!=NULL || jin!=0){
struct ListNode* newNode = (struct ListNode*)malloc(sizeof(struct ListNode));
int val1 = (a==NULL)?0:a->val;
int val2 = (b==NULL)?0:b->val;
newNode->val = val1 + val2+ jin;
newNode->next = NULL;
jin=0;
if(newNode->val >=10){
jin=1;
newNode->val = newNode->val-10;
}
if(s==NULL){
s = newNode;
head =s ;
}
else{
s->next = newNode;
s = s->next;
}
a= (a==NULL)?NULL:a->next;
b= (b==NULL)?NULL:b->next;
}
return doFunc(head);
}
做了整整两个小时,最后的条件判断很重要
5.链表中是否有环?
2.快慢指针,总会追上!!!
bool hasCycle(struct ListNode* head ) {
// write code here
struct ListNode* fast = head;
struct ListNode* slow = head;
if (head == NULL || head->next == NULL) {
return false;
}
// while (fast!= NULL && fast->next != NULL) {
// fast = fast->next->next;
// slow = slow->next;
// if (fast == slow) {
// return true;
// }
// }
//重新写一遍
while(fast!=NULL && fast ->next!=NULL){
fast=fast->next->next;
slow=slow->next;
if(fast==slow){
return true;
}
}
return false;
}
6 第一个环开始的地方?
思维:
1 就是重复出现的第一个地方,只要val取负数就可以!
struct ListNode* EntryNodeOfLoop(struct ListNode* pHead ) {
// write code here
struct ListNode* p = pHead;
// while(fast->next!= NULL && fast!=NULL){
// fast = fast->next->next;
// slow = slow->next;
// if(fast==slow){
// return fast;
// }
// }
while(p!=NULL && p->next !=NULL){
// if(p->val>0){
// p->val = 0-p->val;
// p = p->next;
// }
// else{
// p->val = 0-p->val;
// return p;
// }
if(p->val>0){
p->val = 0-p->val;
p=p->next;
}
else{
p->val = 0-p->val;
return p;
}
}
return NULL;
}
7.倒数第k哥节点?
太简单了,
1 2 3 4 5 6 7 8 9 10
倒数第3个节点就是8,查了2个数,
8.两个链表的第一个公共节点?
太简单了,交叉往后走即可!!!
9.链表相加?复杂!!!
a:1 3 7
b:2 9 6
=
1 4 3 3
先倒过来,再分别加,利用flag记住进位,再return倒过来的现在的p节点!!!
10 归并排序? 复杂!!!
merge先分后治!!!
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类 the head node
* @return ListNode类
*/
struct ListNode* mid(struct ListNode* head) {
struct ListNode* newHead = malloc(sizeof(struct ListNode));
newHead->next = head;
struct ListNode* slow = newHead ;
struct ListNode* fast = newHead;
while (fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
}
struct ListNode* res = slow->next ;
slow->next = NULL;
return res;
}
struct ListNode* merge(struct ListNode* a, struct ListNode* b ) {
struct ListNode* H = (struct ListNode* )malloc(sizeof(struct ListNode));
struct ListNode* p = H;
while (a != NULL && b != NULL) {
if (a->val < b->val) {
p->next = a;
a = a->next;
} else {
p->next = b;
b = b->next;
}
p = p->next ;
}
if (a == NULL) {
p->next = b;
}
if (b == NULL) {
p->next = a ;
}
return H->next;
}
struct ListNode* sortInList(struct ListNode* head ) {
// write code here
//第一步:先给他拆分,各自排序,然后merge直接合并起来
//第二步:时限拆分mid,合并两个算法
//完成主函数
if ( head == NULL || head->next == NULL) {
return head;
}
struct ListNode* leftNode = head;
struct ListNode* rightNode = mid(head);
leftNode = sortInList(leftNode);
rightNode = sortInList(rightNode);
return merge(leftNode, rightNode);
}
11.回文字符串
简单!!!
12.奇数偶数重排??
技巧!!!
struct ListNode* oddEvenList(struct ListNode* head ) {
// write code here
struct ListNode* p1 = head;
struct ListNode* p2 = head->next;
struct ListNode* p3= p2;
if(head ==NULL){
return head;
}
// struct ListNode* p2 = (struct ListNode*)malloc(sizeof(struct ListNode));
while(p2!=NULL && p2->next!=NULL){
p1->next = p2->next;
p1 = p1->next;
p2->next = p1->next;
p2 =p2->next;
}
p1->next = p3;
return head;
}
12.删掉重复的元素?
简单!!!直接往后面跳着就行了
struct ListNode* p = head;
struct ListNode* newHead = malloc(sizeof(struct ListNode));
newHead ->next = head;
int temp = 0;
while (p != NULL) {
temp = p ->val;
while (p->next != NULL && p->next->val == temp) {
p->next = p->next->next;
}
p = p->next;
}
return newHead->next;
13.删掉所有重复的元素??? 复杂
if(head ==NULL || head ->next==NULL){
return head;
}
struct ListNode* newHead = (struct ListNode* )malloc(sizeof(struct ListNode));
newHead ->next = head;
struct ListNode* p = newHead;
while(p->next !=NULL && p->next->next!=NULL){
if( p->next->val==p->next->next->val ){
int temp = p ->next->val;
while(temp == p->next->val && p->next!=NULL){
p->next = p->next->next;
}
}
else{
p = p->next;
}
}
return newHead->next;
2.3 排序算法/二分查找
1.二分查找?简单,吃饭喝水一样。。。。
智商题!!!!!
2.找到波峰元素?
如果mid>mid+1,那么峰在左侧或者mid本身,
else,峰值一定不是她自己!!!
int findPeakElement(int* nums, int numsLen ) {
// write code here
int left = 0 ;
int right = numsLen-1;
while(left<right){
int mid = (left+right)/2;
if(nums[mid]>nums[mid+1]){
right= mid;
}
else{
left = mid+1;
}
}
return right;
}
还有一种方法:
从1到len-1遍历整个数组,如果比两边大,直接返回,然后对0 和len位置,分别考虑即可。。。枝智商题!
3.数组的逆序对?
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param numsLen int nums数组长度
* @return int整型
*/
long long merge(int* nums,int* temp ,int left ,int mid,int right){
//先ikj左右分别处理
int i = left,j=mid+1,k=left;
long long cnt = 0;
while(i<=mid&& j<=right){
if(nums[i]<=nums[j]){
temp[k++] = nums[i++];
}
else{
temp[k++] = nums[j++];
cnt += (mid-i+1);
}
}
while(i<=mid){
temp[k++] = nums[i++];
}
while(j<=right){
temp[k++] = nums[j++];
}
//再把剩下的元素补充道temp
for(int i = left ;i<=right;i++){
nums[i]=temp[i];
}
// 最后再把temp的放到nums里面去
return cnt;
}
long long merge_sort(int* nums,int* temp ,int left,int right ){
long long cnt = 0;
if(left<right){
int mid = (left+right)/2;
cnt += merge_sort(nums, temp, left, mid);
cnt += merge_sort(nums, temp, mid+1, right);
cnt += merge(nums,temp,left,mid,right);
}
return cnt ;
}
int InversePairs(int* nums, int numsLen ) {
// write code here
long long cnt =0;
int* temp = (int*)malloc(numsLen*sizeof(int));
cnt = (long long)merge_sort(nums,temp ,0,numsLen-1 );
return cnt % 1000000007;
}
有难度,有四位模板!!!
归并排序思维
4 旋转数组的最小数字
二分查找!!!
int minNumberInRotateArray(int* nums, int numsLen ) {
// write code here
int left =0 ,right =numsLen-1;
while(left<right){
int mid = (left+right)/2;
if(nums[mid]>nums[right]){
left =mid+1;
}
else if(nums[mid]<nums[right]){
right =mid;
}
else{
right--;
}
}
return nums[right];
}
2.4 栈/队列
1有效序列括號?
()[]{}這種情況下,哪些是有效的括號?
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串
* @return bool布尔型
**/
bool isValid(char* s ) {
// write code here
// char stack[1000];
char* stack = (char* )malloc(10000*sizeof(char));
int top = -1;
int len = strlen(s);
if(len%2!=0){
return false;
}
if(len==0){
return true;
}
for(int i = 0 ;i<len;i++){
if(s[i]=='(' || s[i]=='{'|| s[i]=='['){
stack[++top] = s[i];
}
else {
if(top==-1){
return false;
}
char x = stack[top--];
if( ( s[i]==')'&& x!='(' ) || (s[i]=='}'&&x!='{' )
||( s[i]==']'&&x!='[') )
{
return false;
}
}
}
return top==-1;
}
2 包含min的栈?
c语言直接用两个stack,一个普通的,一个min_stack
进去时候,判断一下min_stack是不是最小的?
static int stack[300],min_stack[300];
static int s_top = 0 ,m_top = 0;
void push(int value ) {
// write code here
if(m_top == 0 ){
min_stack[m_top++] = value;
}
else{
if(value<=min_stack[m_top-1]){
min_stack[m_top++]= value;
}
}
stack[s_top++]= value;
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param 无
* @return 无
*/
void pop() {
// write code here
if(stack[s_top-1]==min_stack[m_top-1]){
m_top--;
}
s_top--;
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param 无
* @return int整型
*/
int top() {
// write code here
return stack[s_top-1];
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param 无
* @return int整型
*/
int min() {
// write code here
return min_stack[m_top-1];
}
3 有效括号序列?
直接strlen求出s的长度
1 如果奇数 ,直接不用算了
2 如果是:( { [ 压进去再说
3.1 如果不是,top==-1 直接失败
3.2 如果栈顶如果不匹配 x = stack[top--]
s[i]=='(' x!=')'
失败!
4 return top ==-1?
4最小的k个数字?
直接冒泡排序
void bubbleSort(int *arr, int length)
{ // 采用最简单的冒泡排序
//两次循环
for(int i = 0 ;i<length-1;i++){
for(int j =0;j<length-i-1;j++){
if(arr[j]>arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] =temp;
}
}
}
}
int *GetLeastNumbers_Solution(int *input, int inputLen, int k, int *returnSize)
{
// write code here
if(k<0 || k>inputLen || input==NULL){
return NULL;
}
int *res = (int *)malloc(10000 * sizeof(int));
// 直接用BubbleSort排序,把指针传进去
bubbleSort(input, inputLen);
for(int i = 0 ;i<k;i++){
res[i]=input[i];
}
*returnSize = k ;
return res;
}
5.第k大的数?快排法!
-1:{
j=left,i=left-1
for(int j =left;j<right)
如果j>i
i++
swap(j, i的元素)
}
0: doFunc1(a, left ,right,k){
如果这一轮的数字正好为k
if(left==right) return left;
pivot = partition(left,right)
否则:
a:partition(a, left,pivot-1)
b:partition(a,pivot+1,right)
}
1:主函数
正常作为接口
6数据的中位数?
7
2.5 哈希法
1.出现次数超过一半的数字?
直接根据hash数组找到里面那些Hash[i]超过1/2Length ,找到了直接返回那个值
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param numbers int整型一维数组
* @param numbersLen int numbers数组长度
* @return int整型
*/
int MoreThanHalfNum_Solution(int* numbers, int numbersLen ) {
// write code here
int hash[100000] = {0};
for(int i= 0 ;i<numbersLen;i++){
hash[numbers[i]]++;
}
for(int i= 0;i<100000;i++){
if(hash[i]>numbersLen/2){
return i;
}
}
// return i;
return 1;
}
2.数组中只出现一次的两个数字:
搞一个hash表就行了
#define MAX_size 1000001
int* FindNumsAppearOnce(int* nums, int numsLen, int* returnSize ) {
int hash[MAX_size] = {0};
// for (int i = 0 ; i < MAX_size; i++) {
// printf("%d\n,", hash[i]);
// }
for (int i = 0 ; i < numsLen; i++) {
hash[nums[i]]++;
}
int* res = (int*)malloc(2*sizeof(int));
int cnt = 0;
*returnSize =2;
for (int i = 0; i < numsLen; i++) {
if (hash[nums[i]] == 1) {
res[cnt++] = nums[i];
if (cnt == 2) {
break;
}
}
}
if (res[0] > res[1]) {
int t = res[0];
res[0] = res[1];
res[1] = t ;
}
return res;
}
3.缺失的第一个最小的正整数?undone!!!
直接用辅助的存一下出现过的!

int minNumberDisappeared(int* nums, int numsLen ) {
// write code here
int* arr = (int*)malloc(100000 * sizeof(int));
int i = 0;
for ( i = 0 ; i < numsLen; i++) {
arr[i] = 0;
}
for ( i = 0 ; i < numsLen; i++) {
if (nums[i] > 0 && nums[i] <=numsLen) {
arr[nums[i]-1] = 1;
}
}
for (i=0; i < numsLen; i++) {
if (arr[i] == 0) {
break;
}
}
return i + 1;
}
2. 6 递归/回溯
1.有重复的数字序列全排列?
这个题目初看上去很复杂,确实做的时候也比较麻烦,初学者看到直接蒙蔽了,绕来绕去;
本人写这个题目的时候用了将近2哥小时才看明白1,2,3这个序列简单过程的排序方法和过程:


循环的两次过程:

整个运行过程:
运行过程
初始调用
在 permute 函数中,会调用 backtrack(num, 0, numLen - 1, &result, returnSize),这里 num = [1, 2, 3],start = 0,end = 2,result 是用于存储所有排列的二维数组,count 初始值为 0。
第一次调用 backtrack
参数:nums = [1, 2, 3],start = 0,end = 2。
判断条件:start 不等于 end,进入 else 分支。
循环过程:
i = 0 时:
交换元素:调用 swap(&nums[0], &nums[0]),数组不变,仍为 [1, 2, 3]。
递归调用:调用 backtrack(nums, 1, 2, result, count)。
第二次调用 backtrack
参数:nums = [1, 2, 3],start = 1,end = 2。
判断条件:start 不等于 end,进入 else 分支。
循环过程:
i = 1 时:
交换元素:调用 swap(&nums[1], &nums[1]),数组不变,还是 [1, 2, 3]。
递归调用:调用 backtrack(nums, 2, 2, result, count)。
第三次调用 backtrack
参数:nums = [1, 2, 3],start = 2,end = 2。
判断条件:start 等于 end,进入 if 分支。
操作过程:
分配内存:(*result)[*count] = (int *)malloc((end + 1) * sizeof(int)); 为当前排列分配内存。
复制排列:通过 for 循环将 nums 数组的元素复制到 (*result)[*count] 中,也就是把 [1, 2, 3] 存到 result 里。
增加计数:(*count)++,此时 count 变为 1。
回到第二次调用的 backtrack
回溯操作:调用 swap(&nums[1], &nums[1]),数组仍为 [1, 2, 3]。
循环继续:
i = 2 时:
交换元素:调用 swap(&nums[1], &nums[2]),数组变为 [1, 3, 2]。
递归调用:调用 backtrack(nums, 2, 2, result, count)。
第四次调用 backtrack
参数:nums = [1, 3, 2],start = 2,end = 2。
判断条件:start 等于 end,进入 if 分支。
操作过程:
分配内存:为当前排列分配内存。
复制排列:把 [1, 3, 2] 存到 result 中。
增加计数:(*count)++,此时 count 变为 2。
回到第二次调用的 backtrack
回溯操作:调用 swap(&nums[1], &nums[2]),数组变回 [1, 2, 3]。
回到第一次调用的 backtrack
回溯操作:调用 swap(&nums[0], &nums[0]),数组仍为 [1, 2, 3]。
循环继续:
i = 1 时:
交换元素:调用 swap(&nums[0], &nums[1]),数组变为 [2, 1, 3]。
递归调用:调用 backtrack(nums, 1, 2, result, count)。
参数:nums = [2, 1, 3],start = 1,end = 2。
判断条件:start 不等于 end,进入 else 分支。
循环过程:
i = 1 时:
交换元素:调用 swap(&nums[1], &nums[1]),数组不变,为 [2, 1, 3]。
递归调用:调用 backtrack(nums, 2, 2, result, count)。
参数:nums = [2, 1, 3],start = 2,end = 2。
判断条件:start 等于 end,进入 if 分支。
操作过程:
分配内存:为当前排列分配内存。
复制排列:把 [2, 1, 3] 存到 result 中。
增加计数:(*count)++,此时 count 变为 3。
i = 2 时:
交换元素:调用 swap(&nums[1], &nums[2]),数组变为 [2, 3, 1]。
递归调用:调用 backtrack(nums, 2, 2, result, count)。
参数:nums = [2, 3, 1],start = 2,end = 2。
判断条件:start 等于 end,进入 if 分支。
操作过程:
分配内存:为当前排列分配内存。
复制排列:把 [2, 3, 1] 存到 result 中。
增加计数:(*count)++,此时 count 变为 4。
回溯操作:调用 swap(&nums[1], &nums[2]),数组变回 [2, 1, 3]。
回到第一次调用 backtrack 里的此次递归调用处:
回溯操作:调用 swap(&nums[0], &nums[1]),数组变回 [1, 2, 3]。
i = 2 时:
交换元素:调用 swap(&nums[0], &nums[2]),数组变为 [3, 2, 1]。
递归调用:调用 backtrack(nums, 1, 2, result, count)。
参数:nums = [3, 2, 1],start = 1,end = 2。
判断条件:start 不等于 end,进入 else 分支。
循环过程:
i = 1 时:
交换元素:调用 swap(&nums[1], &nums[1]),数组不变,为 [3, 2, 1]。
递归调用:调用 backtrack(nums, 2, 2, result, count)。
参数:nums = [3, 2, 1],start = 2,end = 2。
判断条件:start 等于 end,进入 if 分支。
操作过程:
分配内存:为当前排列分配内存。
复制排列:把 [3, 2, 1] 存到 result 中。
增加计数:(*count)++,此时 count 变为 5。
i = 2 时:
交换元素:调用 swap(&nums[1], &nums[2]),数组变为 [3, 1, 2]。
递归调用:调用 backtrack(nums, 2, 2, result, count)。
参数:nums = [3, 1, 2],start = 2,end = 2。
判断条件:start 等于 end,进入 if 分支。
操作过程:
分配内存:为当前排列分配内存。
复制排列:把 [3, 1, 2] 存到 result 中。
增加计数:(*count)++,此时 count 变为 6。
回溯操作:调用 swap(&nums[1], &nums[2]),数组变回 [3, 2, 1]。
回到第一次调用 backtrack 里的此次递归调用处:
回溯操作:调用 swap(&nums[0], &nums[2]),数组变回 [1, 2, 3]。
最终结果
经过上述一系列的递归调用和回溯操作,result 数组中存储了 [1, 2, 3]、[1, 3, 2]、[2, 1, 3]、[2, 3, 1]、[3, 2, 1]、[3, 1, 2] 这 6 个排列,count 的值变为 6,表示已经生成了 6 种不同的排列。

2.无重复的数字序列全排列?--- undone
3.岛屿数量:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 判断岛屿数量
* @param grid char字符型二维数组
* @param gridRowLen int grid数组行数
* @param gridColLen int* grid数组列数
* @return int整型
*/
#include <stdio.h>
#include<stdlib.h>
void dfs(char **grid, int i, int j, int row, int col)
{
// 不在范围内,不做处理
if ( i < 0 || i >= row || j < 0 || j >=col ||grid[i][j] == '0')
{
return;
}
// 处理掉为0
grid[i][j] = '0';
// 四个方向搜索
dfs(grid, i - 1, j, row, col);
dfs(grid, i + 1, j, row, col);
dfs(grid, i, j - 1, row, col);
dfs(grid, i, j + 1, row, col);
}
int solve(char **grid, int gridRowLen, int *gridColLen)
{
// write code here
// 直接dfs
int count = 0;
for (int i = 0; i < gridRowLen; i++)
{
for (int j = 0; j < *gridColLen; j++)
{
if (grid[i][j] == '1')
{
dfs(grid, i, j, gridRowLen, *gridColLen);
count++;
}
}
}
return count;
}
int main()
{
char matrix[4][4] = {
{'1', '0', '1', '0'},
{'1', '0', '1', '0'},
{'0', '0', '0', '1'},
{'1', '0', '1', '1'}};
int len = 4;
char** grid = (char** ) malloc(4*sizeof(char*));
for(int i=0 ;i<4;i++){
grid[i]= (char*)malloc(4*sizeof(char));
}
// for(int i =0;i<4;i++){
// for(int j =0;j<4;j++){
// printf("%d %d的元素是:%c \n",i,j,grid[i][j]);
// }
// printf("\n");
// }
for(int i = 0;i<4;i++){
for(int j =0;j<4;j++){
grid[i][j] = matrix[i][j];
}
}
printf("正在这里运行呢\n");
printf("岛屿数量:%d\n", solve(grid, 4, &len));
return 0;
}
4 字符串的排列
#include <stdio.h>
#include <stdlib.h>
// 交换两个整数的值
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// 回溯函数,生成所有排列
void backtrack(int *num, int start, int end, int ***result, int *count)
{
// if (start == end) {
// // 当start等于end时,说明已经生成了一个排列
// (*result)[*count] = (int*)malloc((end + 1) * sizeof(int));
// for (int i = 0; i <= end; i++) {
// (*result)[*count][i] = nums[i];
// }
// (*count)++;
// } else {
// for (int i = start; i <= end; i++) {
// // 交换元素
// swap(&nums[start], &nums[i]);
// // 递归生成下一个排列
// backtrack(nums, start + 1, end, result, count);
// // 回溯,恢复原始状态
// swap(&nums[start], &nums[i]);
// }
// }
if (start == end)
{
(*result)[*count] = (int*) malloc((end+1)*sizeof(int));
for(int i = 0;i<=end;i++){
(*result)[*count][i] = num[i];
}
for(int i = 0 ;i<=end;i++){
printf("在这个第%d个序列中,%d个数字是:%d \n ",*count+1,i,(*result)[*count][i]);
// printf("----总结:这个序列中:");
// printf("%d", (*result)[*count][i]);
}
printf("\n\n 接下来打印一个这个%d个序列完整的序列:\n",*count);
for(int i =0;i<=end;i++){
printf("%d - ",(*result)[*count][i]);
}
printf("\n\n");
(*count)++;
}
else
{
for (int i = start; i <= end; i++)
{
swap(&num[start], &num[i]);
backtrack(num, start + 1, end, result, count);
swap(&num[start], &num[i]);
}
}
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param num int整型一维数组
* @param numLen int num数组长度
* @return int整型二维数组
* @return int* returnSize 返回数组行数
* @return int** returnColumnSizes 返回数组列数
*/
int **permute(int *num, int numLen, int *returnSize, int **returnColumnSizes)
{
// 计算排列的总数
// int factorial = 1;
// for (int i = 1; i <= numLen; i++) {
// factorial *= i;
// }
// // 分配内存
// int** result = (int**)malloc(factorial * sizeof(int*));
// *returnColumnSizes = (int*)malloc(factorial * sizeof(int));
// *returnSize = 0;
// // 调用回溯函数
// backtrack(num, 0, numLen - 1, &result, returnSize);
// // 设置每个排列的长度
// for (int i = 0; i < *returnSize; i++) {
// (*returnColumnSizes)[i] = numLen;
// }
// return result;
int sizeCount = 1;
for (int i = 1; i <= numLen; i++)
{
sizeCount *= i;
}
int **res = (int **)malloc(sizeCount * sizeof(int *));
*returnColumnSizes = (int *)malloc(sizeCount * sizeof(int));
*returnSize = 0;
backtrack(num, 0, numLen - 1, &res, returnSize);
for (int i = 0; i < *returnSize; i++)
{
(*returnColumnSizes)[i] = numLen;
}
return res;
}
int main(){
int arr[] = {1,2,3,4,5,6};
// printf("运算后:",permute)
// int** res = (int**) malloc(24*sizeof(int*));
// for(int i = 0 ;i<24;i++){
// *res = (int* )malloc(4*sizeof(int));
// }
int returnSize = 0 ;
// *returnSize = 1;
int len = sizeof(arr)/sizeof(arr[0]);
int* returnColumnSizes= NULL;
int** res = NULL;
res = permute(arr,len,&returnSize,&returnColumnSizes);
return 0;
}
5 括号生成:
/**
* 浠g爜涓殑绫诲悕銆佹柟娉曞悕銆佸弬鏁板悕宸茬粡鎸囧畾锛岃鍕夸慨鏀癸紝鐩存帴杩斿洖鏂规硶瑙勫畾鐨勫€煎嵆鍙�
*
*
* @param n int鏁村瀷
* @return string瀛楃涓蹭竴缁存暟缁�
* @return int* returnSize 杩斿洖鏁扮粍琛屾暟
*/
#include <stdio.h>
#include<stdlib.h>
#include<string.h>
void doFunc(char **res, int *returnSize, char *current,int pos ,int left, int right, int len)
{
if (left == len && right == len)
{
//鍒涘缓space
res[*returnSize] = (char*)malloc((len*2+1) * sizeof(char));
strcpy(res[*returnSize],current);
(*returnSize)++;
return ;
}
if (left<len)
{
//杩欓噷瑕佹槸瀛楃涓�
// #self vip
current[pos] = '(';
doFunc(res,returnSize,current,pos+1,left+1,right,len);
//瀛楃涓蹭骇鐘妔trlen
// current[strlen(current)-1]= '\0';
}
if (right<left)
{
current[pos] = ')';
doFunc(res,returnSize,current,pos+1,left,right+1,len);
// current[strlen(current)-1] = '\0';
}
}
char **generateParenthesis(int n, int *returnSize)
{
// write code here
printf("寮€濮嬬敓鎴愶紒\n");
int returnCount = 1 << (2 * n);
*returnSize = 0;
char **res = (char **)malloc(returnCount * sizeof(char *));
char *current = (char *)malloc(2 * n + 1 * sizeof(char));
doFunc(res, returnSize, current,0, 0, 0, n);
return res;
}
int main()
{
int len =4 ;
int returnSize;
char** res = generateParenthesis(len,&returnSize);
for(int i = 0 ;i<returnSize;i++){
printf("%s \n",res[i]);
}
return 0;
}
6 矩阵最长递增路径
// 矩阵最长递增路径
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 递增路径的最大长度
* @param matrix int整型二维数组 描述矩阵的每个数
* @param matrixRowLen int matrix数组行数
* @param matrixColLen int* matrix数组列数
* @return int整型
*/
#include<stdio.h>
#include<stdlib.h>
int dir[4][2] = {
{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int dfs(int **m, int **memo, int x, int y, int r, int *c)
{
if (memo[x][y] != 0)
{
return memo[x][y];
}
int maxLen = 1;
for (int i = 0; i < 4; i++)
{
int x1 = x + dir[i][0];
int y1 = y + dir[i][1];
if (x1 >= 0 && x1 < r && y1 >= 0 && y1 < *c && m[x1][y1] > m[x][y])
{
int len = 1 + dfs(m, memo, x1, y1, r, c);
if (len > maxLen)
{
maxLen = len;
}
}
}
memo[x][y] = maxLen;
return memo[x][y];
}
int solve(int **matrix, int matrixRowLen, int *matrixColLen)
{
// write code here
int maxLen = 1;
int r = matrixRowLen;
int *c = matrixColLen;
int **memo = (int **)malloc(r * sizeof(int *));
for (int i = 0; i < r; i++)
{
memo[i] = (int *)malloc((*c) * sizeof(int));
}
for(int i = 0 ;i<r;i++){
for(int j = 0 ;j<*c;j++){
memo[i][j] = 0;
}
}
for (int i = 0; i < r; i++)
{
for (int j = 0; j < *c; j++)
{
int len = dfs(matrix, memo, i, j, r, c);
if (len > maxLen)
{
maxLen = len;
}
}
}
return maxLen;
}
int main()
{
int arr[][4] = {
{1, 2, 3,4},
{4, 5, 6,5},
{7, 8, 9,47}
};
int r = sizeof(arr)/sizeof(arr[0]);
int c = sizeof(arr[0]) / sizeof(arr[0][0]);
int **matrix = (int **)malloc(r*sizeof(int*));
for(int i = 0;i<r;i++){
matrix[i] = arr[i];
}
// int** memo[ ;
printf("%d \n", solve(matrix, r, &c));
}
2.7 动态规划- 核心:

1斐波那契数列
智商题
老子来手写:
if(n=1
return 1 ;
if(n=2
return 1 ;
else:
return f(n-1 +f(n-2
2 跳台阶:
青蛙往上跳,最小花钱?这个题目:容易有歧义,可以从0或者1 ,那么最好是搞一个len+1的数组,就能用
#include <stdio.h>
// 定义一个函数来返回两个整数中的最小值
int min(int x, int y) {
return x < y ? x : y;
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param cost int整型一维数组
* @param costLen int cost数组长度
* @return int整型
*/
int jumpFloor(int* cost, int costLen) {
// 如果楼梯数量为 0,不需要花费,直接返回 0
if (costLen == 0) {
return 0;
}
// 如果楼梯数量为 1,最小花费就是该台阶的花费
if (costLen == 1) {
return cost[0];
}
// 创建一个数组 dp 来保存爬到每一级台阶的最小花费
int dp[costLen + 1];
// 初始化 dp[0] 和 dp[1] 为 0,因为站在第 0 级和第 1 级台阶不需要额外花费
dp[0] = 0;
dp[1] = 0;
// 从第 2 级台阶开始计算最小花费
for (int i = 2; i <= costLen; i++) {
// 根据状态转移方程计算 dp[i]
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
// 返回爬到第 costLen 级台阶的最小花费
return dp[costLen];
}
3 爬楼梯最小化花费:
描述
给定一个整数数组 cost cost ,其中 cost[i] cost[i] 是从楼梯第i i 个台阶向上爬需要支付的费用,下标从0开始。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
数据范围:数组长度满足 1≤n≤105 1≤n≤105 ,数组中的值满足 1≤costi≤104 1≤costi≤104
示例1
输入:
[2,5,20]
复制返回值:
5
复制说明:
你将从下标为1的台阶开始,支付5 ,向上爬两个台阶,到达楼梯顶部。总花费为5
示例2
输入:
[1,100,1,1,1,90,1,1,80,1]
复制返回值:
6
复制说明:
你将从下标为 0 的台阶开始。 1.支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 2.支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 3.支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 4.支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 5.支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 6.支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。
3.1 这题目也容易看错:
#include <stdio.h>
// 定义一个函数来返回两个整数中的最小值
int min(int a, int b) {
return a < b ? a : b;
}
// 计算到达楼梯顶部的最低花费
int minCostClimbingStairs(int* cost, int costSize) {
// 创建一个长度为 costSize + 1 的数组 dp 来保存到达每个台阶的最小花费
int dp[costSize + 1];
// 初始化 dp[0] 和 dp[1] 为 0,因为可以从第 0 或第 1 个台阶开始,初始花费为 0
dp[0] = 0;
dp[1] = 0;
// 从第 2 个台阶开始计算到达每个台阶的最小花费
for (int i = 2; i <= costSize; i++) {
// 根据状态转移方程更新 dp[i]
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
// 返回到达楼梯顶部(即第 costSize 个台阶)的最小花费
return dp[costSize];
}
4.最长公共子序列?有点小难度 - 容易搞混淆


5 最长公共字串?

要严格相同顺序,不能从中间打断:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* longest common substring
* @param str1 string字符串 the string
* @param str2 string字符串 the string
* @return string字符串
*/
#include<stdio.h>
char* LCS(char* str1, char* str2 ) {
// write code here
// int l1 =strlen(str1);
// int l2 = strlen(str2);
// if(l1==0 || l2 ==0 ){
// return NULL;
// }
// int Max = 0,end = 0;
// int dp[5001][5001] = {0};
// for(int i =1 ;i<=l1;i++){
// for(int j=1;j<=l2;j++){
// if(str1[i-1]==str2[j-1]){
// dp[i][j]=dp[i-1][j-1]+1;
// if(dp[i][j]>Max){
// end = i-1;
// Max = dp[i][j] ;
// }
// }
// else{
// dp[i][j]=0;
// }
// }
// }
// //存到了产犊Max end结束的位置
// char* res = (char* )malloc(sizeof(char)*3000);
// for(int i = 0;i<Max;i++){
// res[i]= str1[end-Max+1+i];
// }
// res[Max]='\0';
// return res;
//最长公共子串,两个位置的必须相同,不然直接跳过为0
int len1 = strlen(str1) , len2 = strlen(str2);
int dp[len1+1][len2+1] ;
dp[0][0] = 0 ;
int maxLen = 0;
int endPos = 0;
for(int i=1;i<=len1;i++){
for(int j =1;j<=len2;j++){
if(str1[i-1]==str2[j-1]){
dp[i][j] = dp[i-1][j-1]+1;
if(dp[i][j]>maxLen){
endPos = i;
maxLen = dp[i][j];
}
}
else{
dp[i][j]=0;
}
}
}
endPos-=1;
char* res = (char*)malloc(5001*sizeof(char));
for(int i = 0;i<maxLen;i++){
res[i] = str1[endPos-maxLen+i];
}
res[maxLen] = '\0';
return res;
}
6 不同路径数量?

/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n ) {
// write code here
// int dp[m+1][n+1];
// for(int i =0;i<m+1;i++){
// dp[i][0]=1;
// }
// for(int i = 0;i<n+1;i++){
// dp[0][i]=1;
// }
// for(int i=1;i<m+1;i++){
// for(int j = 1;j<n+1;j++){
// dp[i][j]=dp[i-1][j]+dp[i][j-1];
// }
// }
// return dp[m][n];
// 从左上到右下
int dp[m][n];
for(int i =0;i<m;i++){
dp[i][0] = 1;
}
for(int j =0;j<n;j++){
dp[0][j]= 1;
}
for(int i =1;i<m;i++){
for(int j =1;j<n;j++){
dp[i][j]= dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
7 矩阵最小路径和:
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
数据范围: 1≤n,m≤5001≤n,m≤500,矩阵中任意值都满足 0≤ai,j≤1000≤ai,j≤100
要求:时间复杂度 O(nm)O(nm)
例如:当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时,对应的返回值为12,
所选择的最小累加和路径如下图所示:

#include<stdio.h>
int min (int a , int b ){
return a<b?a:b;
}
int minPathSum(int** matrix, int matrixRowLen, int* matrixColLen ) {
// write code here
// if(matrixRowLen == 0){
// return 0 ;
// }
// int dp[matrixRowLen][*matrixColLen];
// int minV=100000000;
// dp[0][0] = matrix[0][0];
// for(int i =1;i<matrixRowLen;i++){
// dp[i][0]= dp[i-1][0]+matrix[i][0];
// }
// for(int j =1;j<*matrixColLen;j++){
// dp[0][j]=dp[0][j-1] + matrix[0][j];
// }
// for(int i =1 ;i<matrixRowLen;i++){
// for(int j =1;j<*matrixColLen;j++){
// dp[i][j] = min(dp[i-1][j],dp[i][j-1])+matrix[i][j];
// if(dp[i][j]<minV){
// minV = dp[i][j];
// }
// }
// }
// return dp[matrixRowLen-1][*matrixColLen-1];
int dp[matrixRowLen][*matrixColLen];
dp[0][0] = matrix[0][0];
for(int i =1;i<matrixRowLen;i++){
dp[i][0] = dp[i-1][0]+matrix[i][0];
}
for(int i=1;i<*matrixColLen;i++){
dp[0][i] = dp[0][i-1]+matrix[0][i];
}
for(int i=1 ;i<matrixRowLen;i++){
for(int j =1;j<*matrixColLen;j++){
dp[i][j]= min(dp[i-1][j],dp[i][j-1])+matrix[i][j];
}
}
return dp[matrixRowLen-1][*matrixColLen-1];
}
// int main (){
// return 0 ;
// }
8 BM69 把数字翻译成字符串--undone
9 换零钱
给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个aim,代表要找的钱数,求组成aim的最少货币数。
如果无解,请返回-1.
数据范围:数组大小满足 0≤n≤100000≤n≤10000 , 数组中每个数字都满足 0<val≤100000<val≤10000,0≤aim≤50000≤aim≤5000
要求:时间复杂度 O(n×aim)O(n×aim) ,空间复杂度 O(aim)O(aim)。
输入:[5,2,3],20
复制返回值:4
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 最少货币数
* @param arr int整型一维数组 the array
* @param arrLen int arr数组长度
* @param aim int整型 the target
* @return int整型
*/
int min(int a, int b)
{
return a < b ? a : b;
}
int minMoney(int *arr, int arrLen, int aim)
{
// write code here
int maxLen = aim + 1;
int dp[aim + 1];
dp[0] = 0;
for (int i = 1; i <= aim; i++)
{
dp[i] = aim + 1;
}
// 随你怎么变 总会比aim+1小
// for (int i = 1; i <= aim; i++)
// {
// for (int j = 0; j < arrLen; j++)
// {
// if (i >= arr[j])
// {
// dp[i] = min(dp[i], dp[i - arr[j]] + 1);
// }
// }
// }
for (int i = 1; i <= aim; i++)
{
for (int j = 0; j < arrLen; j++)
{
if (i >= arr[j])
{
dp[i] = min(dp[i], dp[i - arr[j]] + 1);
}
}
}
if (dp[aim] == aim + 1)
{
return -1;
}
return dp[aim];
}
要么就是dp[i 要么就是dp[ i-arr[j] ] +1 ,要么用你原来的,要么少了点 我来凑一张出来,
从1 - aim,123456789.......aim 一个个的试燕! 最终总能使出来
10 最长上升子序列?

#include <stdio.h>
int main()
{
int arr[] = {47, 89, 23, 76, 12, 55, 34, 91, 62, 7, 38, 81, 44, 50, 99};
printf("最长上升子序列是:%d\n\n", LTS(arr, 15));
printf("最长上升子序列是\n");
return 0;
}
int LTS(int *arr, int arrLen)
{
int dp[arrLen];
if (arrLen == 0)
{
return 0;
}
for (int i = 0; i < arrLen; i++)
{
dp[i] = 1;
}
dp[0] = 1;
int maxLen = 1;
// for (int i = 1; i < arrLen; i++)
// {
// for (int j = 0; j < i; j++)
// {
// if (arr[i] > arr[j])
// {
// if (dp[j] + 1 > dp[i])
// {
// dp[i] = dp[j] + 1;
// }
// }
// }
// if (dp[i] > maxLen)
// {
// maxLen = dp[i];
// }
// }
for(int i =1;i<arrLen;i++){
for(int j = 0 ;j<i;j++){
if(arr[i]>arr[j]){
if(dp[j]+1>dp[i]){
dp[i] = dp[j]+1;
}
}
}
if(dp[i]>maxLen ){
maxLen = dp[i];
}
}
return maxLen;
}
11 最长回文子串

每一个遍历,要么是doFunc(i,i) 要么是都Func(i,i+1)
#include <stdio.h>
#include<math.h>
#include<string.h>
int doFunc(char *A, int left, int right)
{
// 从left和right开始一个个往两边拓展,用一个cnt计数
// int len = strlen(A);
// int cnt = 0, flag = 0;
// if (left == right)
// {
// cnt = 1;
// left--;
// right++;
// }
// while (A[left] == A[right] && left >= 0 && right < len)
// {
// cnt += 2;
// left--;
// right++;
// }
// return cnt;
//最开始一个都没有,绝对是0
int res =0;
//中间相等bab 、 不相等baab
if(left==right){
res =1;
left-=1;
right+=1;
}
// int len = strLen(A);
int len = strlen(A);
while(A[left]==A[right] && left>=0 && right<len ){
res+=2;
left-=1;right+=1;
}
return res;
}
int max(int a, int b)
{
return a > b ? a : b;
}
int getLongestPalindrome(char *A)
{
// write code here
// dp方法:初始状态 - 装填转移 - 边界条件
// 干活的函数: s , left , right
// mid 开始,left -1 ,right+1 向两边拓展
// 主函数,从0到右边,一个个找,
// #self 从左边开始一个个找
// int maxLen = 1;
// int len = strlen(A);
// if (len == 0)
// {
// return 0;
// }
// int r1, r2;
// for (int i = 0; i < len; i++)
// {
// r1 = doFunc(A, i, i);
// r2 = doFunc(A, i, i + 1);
// int res = max(r1, r2);
// if (res > maxLen)
// {
// maxLen = res;
// }
// }
// return maxLen;
int maxLen = 1;
int len = strlen(A);
for(int i =0;i<len;i++){
int res1= doFunc(A,i,i);
int res2 = doFunc(A,i,i+1);
int res = max(res1,res2);
if(res>maxLen) maxLen =res;
}
return maxLen;
}
// int main()
// {
// int i = doFunc2();
// return 0;
// }
12 数字字符串转化成IP地址---undone
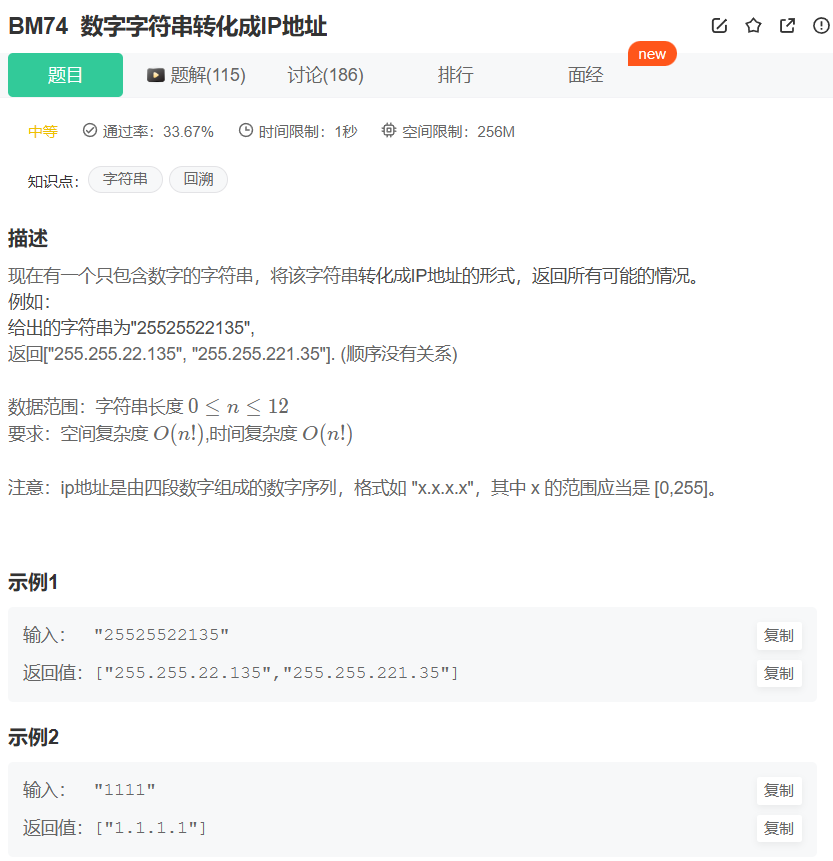
13 编辑距离(一)
给定两个字符串 str1 和 str2 ,请你算出将 str1 转为 str2 的最少操作数。
你可以对字符串进行3种操作:
1.插入一个字符
2.删除一个字符
3.修改一个字符。
字符串长度满足 1≤n≤1000 1≤n≤1000 ,保证字符串中只出现小写英文字母。
14 编辑距离

/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param numsLen int nums数组长度
* @return int整型
*/
#include<stdio.h>
int max(int a ,int b ){
return a>b?a:b;
}
int rob(int* nums, int numsLen ) {
// write code here
//打家劫舍问题:要么搞nums[i]+dp[i-2] ,要么dp[i-1]
int dp[numsLen] ;
dp[1] =max(nums[0],nums[1]);
dp[0] = nums[0];
for(int i=2;i<numsLen;i++){
dp[i] = max(dp[i-1],nums[i]+dp[i-2]);
}
return dp[numsLen-1];
}
int main(){
int a[] = {12, 9,6,6,7,7,4,5,3,7,3,3,7,5,23,6,2,36,26,4,23,6,2,36,24,36,3,68,8 ,12};
int len = sizeof(a)/sizeof(a[0]);
printf("结果是:%d \n",rob(a,len));
}
15 打家劫舍2 - 环形的打劫
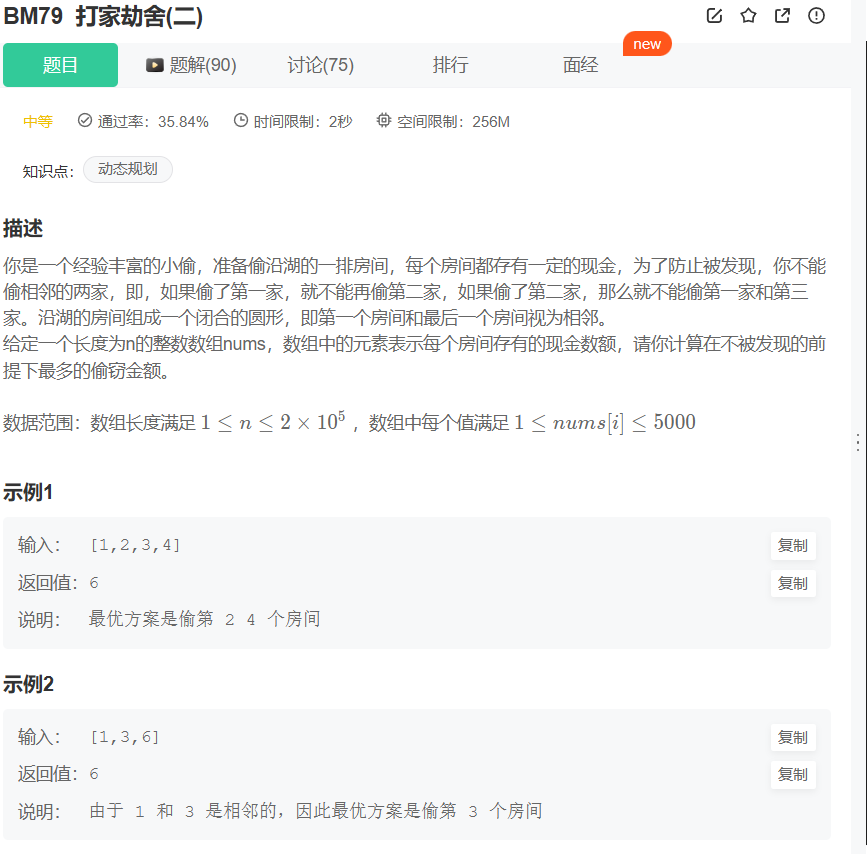
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param numsLen int nums数组长度
* @return int整型
*/
#include<stdio.h>
int max(int a ,int b ){
return a>b?a:b;
}
int doFunc(int* a,int start ,int end){
if(start == end){
return a[start];
}
int dp[end-start+1 ];
dp[0] = a[start];
dp[1]= max(a[start],a[start+1]);
for(int i =2;i<=end-start;i++){
dp[i] = max(dp[i-1],dp[i-2]+a[i+start]);
}
return dp[end-start];
}
int rob(int* nums, int numsLen ) {
// write code here
//带了环形结构的打家劫舍:
int res1= doFunc(nums,0,numsLen-2);
int res2 =doFunc(nums,1,numsLen-1);
return res1>res2?res1:res2;
}
int main(){
int a[ ]= {1,4,5,65,65,4,7,2,8,2,18,3,8,1,1,4,2,7,2,2,7,1,12};
int len = sizeof(a)/sizeof(a[0]);
printf("%d \n",rob(a,len));
}
2.8 字符串
0目录
1 字符串变形
2 最长公共前缀
3 验证ip
4大数加法
2.9 双指针
0 目录
1 判断是否为回文字符串
2 合并区间
3 反转字符串
4 最长无重复子数组
5 盛水最多的容器
2.10 贪心
1 主持人压榨问题
#include <stdio.h>
#include <stdlib.h>
// 比较函数,用于qsort排序
int compare(const void *a, const void *b) {
return (*(int *)a - *(int *)b);
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 计算成功举办活动需要多少名主持人
* @param n int整型 有n个活动
* @param startEnd int整型二维数组 startEnd[i][0]用于表示第i个活动的开始时间,startEnd[i][1]表示第i个活动的结束时间
* @param startEndRowLen int startEnd数组行数
* @param startEndColLen int* startEnd数组列数
* @return int整型
*/
int minmumNumberOfHost(int n, int** startEnd, int startEndRowLen, int* startEndColLen ) {
// 分离开始时间和结束时间
// int *start_times = (int *)malloc(n * sizeof(int));
// int *end_times = (int *)malloc(n * sizeof(int));
// for (int i = 0; i < n; i++) {
// start_times[i] = startEnd[i][0];
// end_times[i] = startEnd[i][1];
// }
// // 对开始时间和结束时间进行排序
// qsort(start_times, n, sizeof(int), compare);
// qsort(end_times, n, sizeof(int), compare);
// // 初始化指针和计数器
// int start_index = 0;
// int end_index = 0;
// int max_hosts = 0;
// int current_hosts = 0;
// // 遍历时间点
// while (start_index < n) {
// if (start_times[start_index] < end_times[end_index]) {
// // 有新活动开始
// current_hosts++;
// start_index++;
// } else {
// // 有活动结束
// current_hosts--;
// end_index++;
// }
// // 更新最大主持人数量
// if (current_hosts > max_hosts) {
// max_hosts = current_hosts;
// }
// }
// // 释放动态分配的内存
// free(start_times);
// free(end_times);
// return max_hosts;
int* starttimes = (int*)malloc(n*sizeof(int));
int* endtimes = (int*)malloc(n*sizeof(int));
for(int i= 0;i<n;i++){
starttimes[i] = startEnd[i][0];
endtimes[i] = startEnd[i][1];
}
qsort(starttimes,4,sizeof(int),compare);
qsort(endtimes,4,sizeof(int),compare);
int start_index = 0 ,end_index= 0,count = 0,maxCount = 0;
while(start_index<n){
if(starttimes[start_index ] < endtimes[end_index]){
start_index++;
count++;
}
else{
end_index++;
count--;
}
if(count>maxCount){
maxCount = count;
}
}
return maxCount;
}
int main(){
int arr[4][2] ={{0,2},{0,3},{1,2},{2,5}};
int* startend[4];
for(int i =0;i<4;i++){
startend[i] = arr[i];
}
int x =2 ;
printf("%d \n",minmumNumberOfHost(4,startend,4,&x));
}
2.11 模拟算法
3 个人的一点小总结
1 小小的学习建议:
-
体系化学习基础知识:要肯吃苦!
-
熟能生巧:做多了比如说我个人在做到第三遍到第四遍的时候突然就感觉动归何必归本质都是一样的无非就是前一个状态到后一个状态的分类找规律;当时我印象特别深刻天天做的时候昏头胀脑的反正就这么做一点但是碰到最长递增子序列和最长无重复子序列后,突然感觉背后的逻辑是一模一样的,无非就是变换了几个条件和规律但是对I和J DP这个思维的抽象却是一样的这种感觉非常奇妙只有当自己敲多了你才能够有这种感觉
-
定期在大佬的帖子底下留言和大佬加微信共同刷题,一起学习,找到进步的感觉
2 我的一点小小的刷题法,可以参考
| 阶段 | 时间点 | 目标 | 关键动作 |
|---|---|---|---|
| 第 1 遍 | 当天 | 理解题意 | 不看题解 |
| 第 2 遍 | 3 天后 | 优化代码 + 总结 | 对比官方题解 找不同 |
| 第 3 遍 | 1 周后 | 脱离模板 | 用不同语言 /实现 |
| 第 4 遍 | 1 月后 | 复杂度分析 | 重点突破卡壳的边界 |
| 第 5 遍 | 面试前 | 限时训练 | 用手机计时,模拟真实面试场景 |
3. 错题本
- 思维:标注卡壳的步骤
- 陷阱:记录边界条件 比如:空数组 / 单节点处理
- 优化:对比多种解法的时间复杂度: 如O (n²)→O (n log n))
4、小想法发散思维
-
校招:
- 大厂笔试通过率提升 40%(高频题覆盖率达 80%)
- 技术面试中,算法表现占薪资议价权的 30%
-
深耕:
- 分布式系统设计,区块链的一致性算法→Raft/Paxos
- 大数据处理,在大数据开发的海量数据排序→MapReduce 分片策略
-
拓展:
- 算法共享!
- 本人的技术博客可以进一步和大家在学习中!交流效果更好!
5、代码之外
- 简化:复杂问题拆解为子问题:树的后序遍历→左右子树递归
- 逆向:双指针从两端向中间移动,避免 O (n²) 暴力
- 抽象:举个例子就是最简单的那个我在开头提到的那个模板序列问题这场地震子序列最长无重复子序列最长无重复数组最长递增路径最长无重复,对这种模板问题起码在热题一百里能找到十个以上其实事后想想完全都可以抽象为一个通用的方法:编辑距离→二维 DP 模板)
6 福利
完整代码与思维导图已整理至:我自己的GitHub 仓库+ 优快云 博客,关注我私信我发给大家!
关注后私信「算法」,获取《算法面试高频题 TOP101》PDF 版,你们有我自己亲自在本地vs code运行过的两万多行代码结合二十万行注释和这个帖子的六万自述的详细总结。啥也不多说了就说我到底值不值得你拥有,哈哈哈哈,不多说了大家刷起来吧!!!
























 85
85

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








