反向传播算法（BP）python实现

前言

本文所用的数据集来自 西瓜书P150-154西瓜数据3.0，实现了一个单隐含层单输出的网络，不使用sklearn库直接训练，文章末尾会附上完整代码和数据集。

一、BP算法简介及其实现步骤

BP算法基于梯度下降法，通过计算损失函数关于网络中各层权重和偏置的梯度，逐层反向传播误差，从而更新参数以减少预测误差。 

注意：

偏置的主要作用是为激活函数提供一个平移，使得模型能够更好地拟合数据。即使输入的所有特征为零，偏置也能确保神经元有一个非零的输出。

而阈值通常是用于激活函数的阈值判断条件，决定一个神经元是否被激活或激活的程度。

两者在计算上略有区别，偏置项一般是被加上再传入激活函数中，而阈值再被传入时要被减去，在更新参数时求导的正负会有变化。

                                   

学习过程：

        前向传播：输入数据通过网络，经过每一层的加权和非线性激活函数，输出预测结果。

        误差计算：使用损失函数计算预测结果与真实标签之间的误差。

        反向传播：从输出层开始，将误差按链式法则计算并传播回去，逐层计算每个权重的梯度。

        参数更新：利用学习率（通常是一个小的正数）乘以梯度更新权重和偏置。

主要步骤：                    

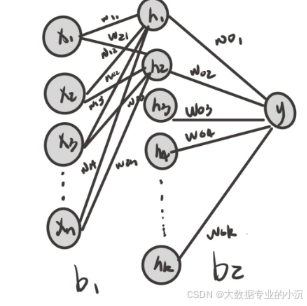
1.初始化：随机初始化神经网络中的连接权重wi（输入层x到隐含层h）、wo（隐含层h到输出层y）、b（偏置，这里对应的有两个）。

2.前向传播（Forward Propagation）：将输入数据送入网络的输入层，通过连接权重和激活函数（这里选择sigmoid函数将值投影到0~1之间），逐层计算各个神经元的输出，直至得到输出层的输出。

                                                   

其中下标i表示各层的输入，o表示各层的输出。

3.计算误差：将输出层的预测结果与真实的目标输出进行比较，计算网络在当前权重下的误差E。这里使用均方误差来表示：

                                                  

y为真实值，yo为神经网络输出的值。

 4.反向传播（Backward Propagation）：根据误差，从输出层开始，按照反向顺序逐层计算每个神经元的梯度。梯度表示误差随着权重的变化而变化的速率。这一步是BP算法的核心，通过链式法则计算梯度，并将误差从输出层反向传播到隐藏层和输入层。

                                  &nbs