C#知识学习-002

1.整型数值类型

1.1 整数数学

int 类型表示 整数、正整数或负整数

每个整型的默认值为零

所有整型数值类型都支持 算术、 按位逻辑、 比较和 相等 运算符，举例：

int a = 18;
int b = 6;
int c = a + b;
Console.WriteLine(c);

1.2 运算顺序

规则与在数学中学到的规则一致，举例：

（我记得老师教的是：先乘除后加减，有括号先算括号）
（顺便带你复习一下上一篇string的知识点）

int a = 5;
int b = 4;
int c = 2;
int d = a + b * c;
Console.WriteLine("d = " + d);

int e = (a + b) * c;
Console.WriteLine($"e = {e}");

补充：即使你期望结果包含小数或分数部分，整数除法始终生成整数结果

int a = 7;
int b = 4;
int c = 3;
int d = (a + b) / c;
Console.WriteLine(d);

 1.3 整数精度和限制

整数除法截断了结果，但是 可以使用余数运算符（字符 %）获取余数：

int a = 7;
int b = 4;
int c = 3;
int d = (a + b) / c;
int e = (a + b) % c;
Console.WriteLine($"quotient: {d}");
Console.WriteLine($"remainder: {e}");

c#中的int类型是有最大最小限制的，你可以通过查看属性（MinValue和MaxValue）获取：

int max = int.MaxValue;
int min = int.MinValue;
Console.WriteLine($"min {min}");
Console.WriteLine($"max {max}");

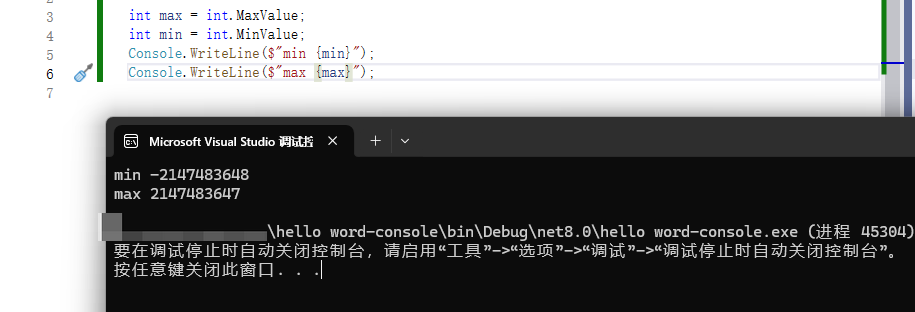
是不是好奇超出了限制会怎么样？（我好奇）

带你验证：

int max = int.MaxValue;
int what = max + 3;
Console.WriteLine($"error: {what}");

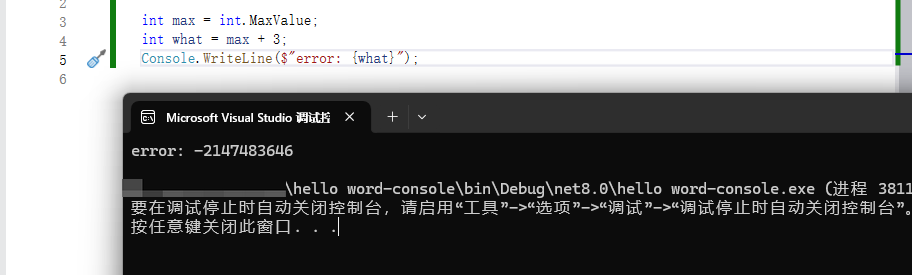
答案非常接近最小（负）整数。 这与 min + 2 相同

 加法运算 溢出了 整数的允许值。 答案是一个大负数

因为溢出会导致整数值从最大可能的值“回绕”到最小值

1.4 整型类型的特征

C# 支持以下预定义整型类型（比较常见的）：

C# 类型/关键字	范围	尺寸	.NET 类型
sbyte	-128 到 127	8 位带符号整数	System.SByte
byte	0 到 255	无符号 8 位整数	System.Byte
short	-32,768 到 32,767	带符号 16 位整数	System.Int16
ushort	0 到 65,535	无符号 16 位整数	System.UInt16
int	-2,147,483,648 到 2,147,483,647	带符号的 32 位整数	System.Int32
uint	0 到 4,294,967,295	无符号 32 位整数	System.UInt32
long	-9,223,372,036,854,775,808 到 9,223,372,036,854,775,807	64 位带符号整数	System.Int64
ulong	0 到 18,446,744,073,709,551,615	无符号 64 位整数	System.UInt64

最左侧列中的每个 C# 类型关键字都是相应 .NET 类型的别名。

关键字和 .NET 类型名称可互换，举例：

int a = 123;
System.Int32 b = 123;

1.5 整数文本

1.5.1 形式

进制	前缀	示例
十进制	无	42
十六进制	0x 或 0X	0x2A（= 42）
二进制	0b 或 0B	0b_0010_1010(=42)

那我就多补充一下，防止大家看晕：

（1）十六进制（Hexadecimal）使用 16 个符号：0-9 表示 0-9，A-F 表示 10-15

• 0x2A 分为两部分：
  • ​​2​​ 是十六进制的十位数 → 2 × 16¹ = 32
  • ​​A​​ 是十六进制的个位数（A 代表 10） → 10 × 16⁰ = 10
  • ​​计算​​：32 + 10 = 42

（2）二进制： （英文Binary）每位表示 2 的幂（从右向左，从 2⁰ 开始）

位位置：7 6 5 4 3 2 1 0 → 幂：2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰

对应值：0 0 1 0 1 0 1 0 → 计算：

2⁵ = 32 → 1 × 32 = 32

2³ = 8 → 1 × 8 = 8

2¹ = 2 → 1 × 2 = 2

其他位为 0，计算​​：32 + 8 + 2 = 42

（3）快速转换技巧​​：

• ​​十六进制 → 二进制​​：每 1 位十六进制 = 4 位二进制
  0x2 → 0010，0xA → 1010 → 合并 00101010
• ​​二进制 → 十六进制​​：每 4 位二进制 = 1 位十六进制
  0010 → 2，1010 → A → 合并 0x2A

1.5.2 数字分隔符 _​​ ：

主要是用于提高可读性，编译器会忽略它

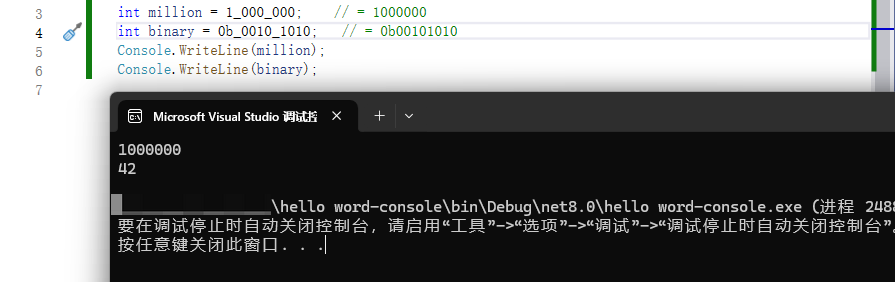
int million = 1_000_000;    // = 1000000
int binary = 0b_0010_1010;   // = 0b00101010
Console.WriteLine(million);
Console.WriteLine(binary);

1.5.3 类型推导

后缀	候选类型顺序	示例	说明
无后缀	int → uint → long → ulong	42 → int	优先选择能容纳值的最小类型
u 或 U	uint → ulong	42U → uint	强制无符号类型
l 或 L	long → ulong	42L → long	优先长整型
ul 等	ulong	42UL → ulong	明确无符号长整型

这里先简单知道有个关键字 var，它可以自动推导出你的值类型

（var 对于写代码会更方便，目前知道有它即可，之后会专门讲它）

那就先举个例子，这样更能理解 var：

var a = 42;         // 无后缀 → 类型为 int
var b = 42U;        // 后缀U → 类型为 uint
var c = 42L;        // 后缀L → 类型为 long
var d = 3000000000; // 无后缀 → 超过int范围(21亿)，自动升为long
var e = 3000000000U; // 后缀U → 类型为uint（30亿在uint范围内）

1.5.4 隐式转换规则

如果文本类型是 int，且值在目标类型范围内，可隐式转换：
sbyte, byte, short, ushort, uint, ulong

举例说明：

byte a = 100;   // 合法：100在byte范围内(0~255)
byte b = 300;   // 编译错误 CS0031：300 > 255

 解决方案：使用显式转换

举例说明：

byte a = (byte)300; // = 44 (溢出截断)
long b = (long)42;  // 显式转换

注：任何整型数值类型都可以隐式转换为任何浮点数值类型 

2.浮点数值类型

浮点数值类型表示实数，浮点数可用于表示可能较大或较小数量的非整数

所有浮点数值类型都支持算术、比较和相等运算符

每个浮点类型的默认值都为零，和int型一样，也有MinValue 和 MaxValue 常量

2.1 特征

以下是常用的：

C# 类型/关键字	大致范围	精度	大小	.NET 类型
float	±1.5 x 10−45 至 ±3.4 x 1038	大约 6-9 位数字	4 个字节	System.Single
double	±5.0 × 10−324 到 ±1.7 × 10308	大约 15-17 位数字	8 个字节	System.Double

2.2 双精度类型

数值 double 类型表示双精度浮点数

双精度 是一个相对术语，用于描述用于存储值的二进制数字数

（专业术语没关系，我给你举例，希望能让你很快看懂）

double a = 5;
double b = 4;
double c = 2;
double d = (a + b) / c;
Console.WriteLine(d);

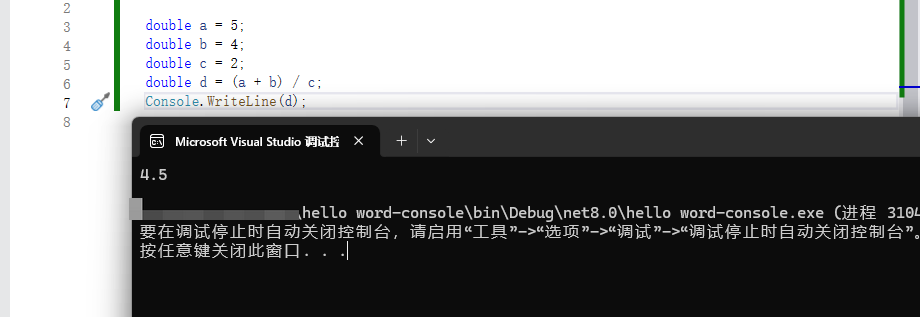
答案包含了小数部分，那试试对双精度类型使用更复杂一点的表达式：

double a = 19;
double b = 23;
double c = 8;
double d = (a + b) / c;
Console.WriteLine(d);

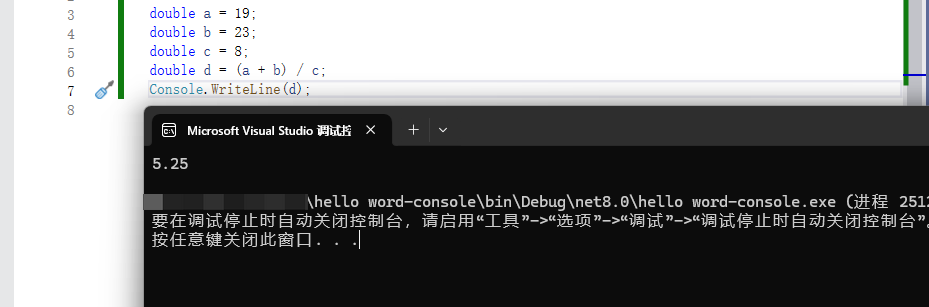
double类型也有最大最小值，获取方法和int类型是一样的：

double max = double.MaxValue;
double min = double.MinValue;
Console.WriteLine($"min {min}");
Console.WriteLine($"max {max}");

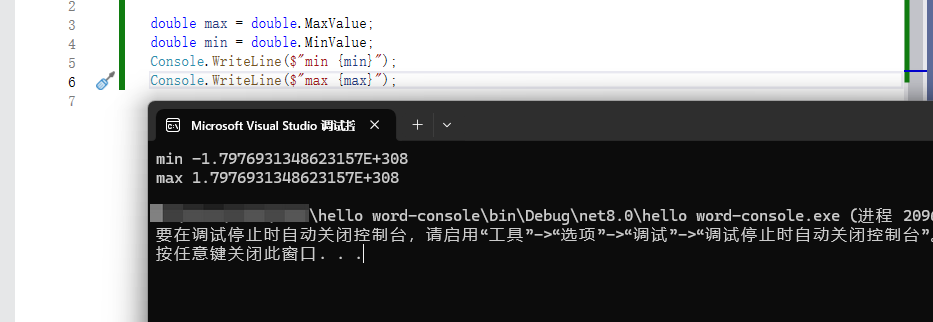
这些值以科学表示法打印。 E 之前的数字有符号。 E 后面的数字是指数，作为 10 的幂

让我再给你说详细点吧：

-1.7976931348623157E+308 表示 -1.7976931348623157 × 10^308

同样，1.7976931348623157E+308 表示 1.7976931348623157 × 10^308

关于误差：

与数学上的十进制数字一样，C# 中的双精度值可能会有四舍五入误差

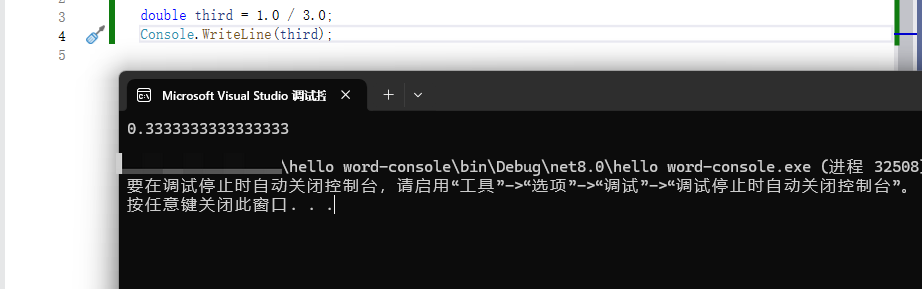
你知道 0.3 是 3/10，而与 1/3 【正确结果】并不完全相同。 同样， 0.33 是 33/100。 该值更接近1/3，但仍不精确。 无论添加多少小数位数，舍入误差仍然存在。

double third = 1.0 / 3.0;
Console.WriteLine(third);

2.3 文本

• 不带后缀的文本或带有 d 或 D 后缀的文本的类型为 double
• 带有 f 或 F 后缀的文本的类型为 float

 举例：

（希望你还记得数字分隔符 _）

double d = 3D;
d = 4d;
d = 3.934_001;

float f = 3_000.5F;
f = 5.4f;

2.4 隐式转换规则

浮点数值类型之间只有一种隐式转换：从 float 到 double。

但是，可以使用​显式强制转换，将任何浮点类型转换为任何其他浮点类型

举例：double 到 float（显式强制转换）

double safeValue = 1234567.59;   // 7位整数+2位小数
float safeFloat = (float)safeValue;

Console.WriteLine(safeValue);
Console.WriteLine(safeFloat);

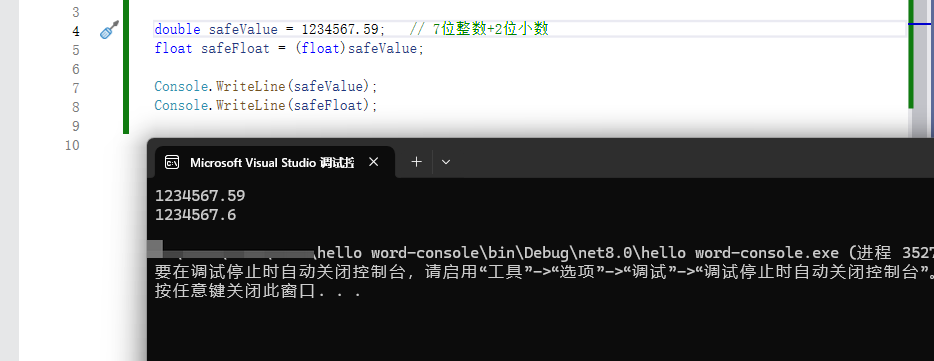
我来解释为什么出现了0.01的精度损失：

这是由于float只能精确存储前7位有效数字（1234567）

对于第8位数字（5）和第9位数字（9），它进行以下处理：

• 四舍五入规则：.59 → .6
• 存储结果为：1234567.6（舍弃了最后一位精度）

​​补充：将浮点数（double 或 float）转换为整数类型​：

​浮点数的小数部分会被​​直接截断​​（不是四舍五入），且结果总是向零靠近：

double a = 3.9;
int b = (int)a;    // 结果 = 3（不是4）

double c = -2.7;
int d = (int)c;    // 结果 = -2（不是-3）

 学到了这里，咱俩真棒，记得按时吃饭（最近给“菠萝”买了新的冻干吃~）

【本篇结束，新的知识会不定时补充】