LeetCode第 191 场周赛（C++）

1、数组中两元素的最大乘积（3分）

问题描述

给你一个整数数组 nums，请你选择数组的两个不同下标i和j，使 (nums[i]-1)*(nums[j]-1)取得最大值。

请你计算并返回该式的最大值。

示例 1：

输入：nums = [3,4,5,2]
输出：12
解释：如果选择下标 i=1 和 j=2（下标从 0 开始），则可以获得最大值，(nums[1]-1)(nums[2]-1) = (4-1) * (5-1) = 34 = 12 。

示例 2：

输入：nums = [1,5,4,5]
输出：16
解释：选择下标 i=1 和 j=3（下标从 0 开始），则可以获得最大值 (5-1)*(5-1) = 16 。

示例 3：

输入：nums = [3,7]
输出：12

提示：

2 <= nums.length <= 500
1 <= nums[i] <= 10^3

解题思路

• 从大到小排序，最大的两个值即可。

代码实现

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        sort(nums.begin(), nums.end(), greater<int>());
        return (nums[0] - 1) * (nums[1] - 1);
    }
};

• 该题目也可以使用set和multimap：其中元素是按照由小到大排列的，所以定义set<int>::reverse_iterator iter = iset.rbegin()等方法来求得元素中的最大值和次大值。但要注意使用reverse_iterator时迭代器由右往左是执行iter++而不是iter--。
• 使用multimap：

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        multimap<int, int> iimap;
        for(auto& i : nums)
            iimap.insert(pair<int, int>(i, 0));
        multimap<int, int>::reverse_iterator iter = iimap.rbegin();
        return (iter++->first - 1) * (iter->first - 1);
	}        
};

• 使用set：

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        multiset<int> iset(nums.begin(), nums.end());
        multiset<int>::reverse_iterator iter = iset.rbegin();
        return (*iter++ - 1) * (*iter - 1);
    }
};

运行截图

2、切割后面积最大的蛋糕（4分）

问题描述

矩形蛋糕的高度为h且宽度为 w，给你两个整数数组horizontalCuts和 verticalCuts，其中horizontalCuts[i]是从矩形蛋糕顶部到第i个水平切口的距离，类似地，verticalCuts[j]是从矩形蛋糕的左侧到第j个竖直切口的距离。

请你按数组horizontalCuts和 verticalCuts中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果对 10^9 + 7取余后返回。

示例 1：

输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示：

2 <= h, w <= 10^9
1 <= horizontalCuts.length < min(h, 10^5)
1 <= verticalCuts.length < min(w, 10^5)
1 <= horizontalCuts[i] < h
1 <= verticalCuts[i] < w
题目数据保证 horizontalCuts 中的所有元素各不相同
题目数据保证 verticalCuts 中的所有元素各不相同

解题思路

• 本题目是由两个数组中的数（1 <= horizontalCuts[i] < h，1 <= verticalCuts[i] < w）将矩形分成若干个子图形，所以两数组（包括矩形边界）中数值间隔最大的乘积就是最大面积。
• C++中的pow(x, y)返回值是double型，参数也是double型。
• 不得不说C++数值超出（int）范围的问题真是太棘手了，两个数相乘，超出int型需要分别转换为long型。这导致RE了10次才AC的。
• getmaxmargin()求数组中两个相邻元素最大间隔时，将数组的大小写成length（此参数是矩形的边长），这是一个极大的低端错误。

代码实现

class Solution {
public:
    int getmaxmargin(int& length, vector<int>& ivec){
        int maxnum = ivec[0];
        for(int i = 1; i < ivec.size(); i++)
            maxnum = max(maxnum, ivec[i] - ivec[i - 1]);
        return max(maxnum, length - ivec.back());
    }
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        long remainder = pow(10, 9) + 7;
        long res = (long)getmaxmargin(h, horizontalCuts) * (long)getmaxmargin(w, verticalCuts);
        return res % remainder;
    }
};

3、重新规划路线（5分）

问题描述

n座城市，从 0到n-1编号，其间共有 n-1条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用connections表示，其中connections[i] = [a, b]表示从城市 a到b的一条有向路线。

今年，城市 0将会举办一场大型比赛，很多游客都想前往城市0。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市0。

示例 1：

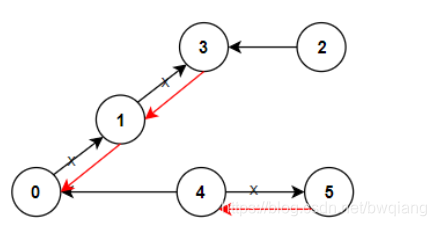
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 2：

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 3：

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

提示：

2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

解题思路