LeetCode 239 滑动窗口最大值（C++）

最新推荐文章于 2024-07-14 17:45:58 发布

bwqiang

最新推荐文章于 2024-07-14 17:45:58 发布

阅读量309

点赞数

CC 4.0 BY-SA版权

分类专栏： LeetCode

本文链接：https://blog.youkuaiyun.com/bwqiang/article/details/105793857

LeetCode 专栏收录该内容

36 篇文章

订阅专栏

本文探讨了在数组中寻找滑动窗口最大值的有效算法，包括基础解法和进阶的线性时间复杂度解法。通过实例展示了如何利用max_element函数和分割数组的方法来解决问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

问题描述

给定一个数组nums，有一个大小为 k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。

进阶：
你能在线性时间复杂度内解决此题吗？

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

解题思路

题目的本意是返回每个滑动窗口中最大值组成的vector容器。
从左向右遍历nums容器。将每次滑动窗口中的最大值存入vector容器后返回该容器。
max_element()函数返回容器中最大值的下标，若需取值，前面加*。
进阶解法：只能抄袭LeetCode上的官方解法了：

代码实现

（1）

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> ivec;
        vector<int>::iterator iter = nums.begin();
        for(; iter != nums.end() - k + 1; iter++) // 注意数组下标的问题
            ivec.push_back(*max_element(iter, iter + k));
        return ivec;
    }
};

实现截图

在这里插入图片描述

进阶解法

这是另一个 $O (N)$ 的算法。本算法的优点是不需要使用 数组 / 列表 之外的任何数据结构。

算法的思想是将输入数组分割成有 $k$ 个元素的块。
若 n % k != 0，则最后一块的元素个数可能更少。

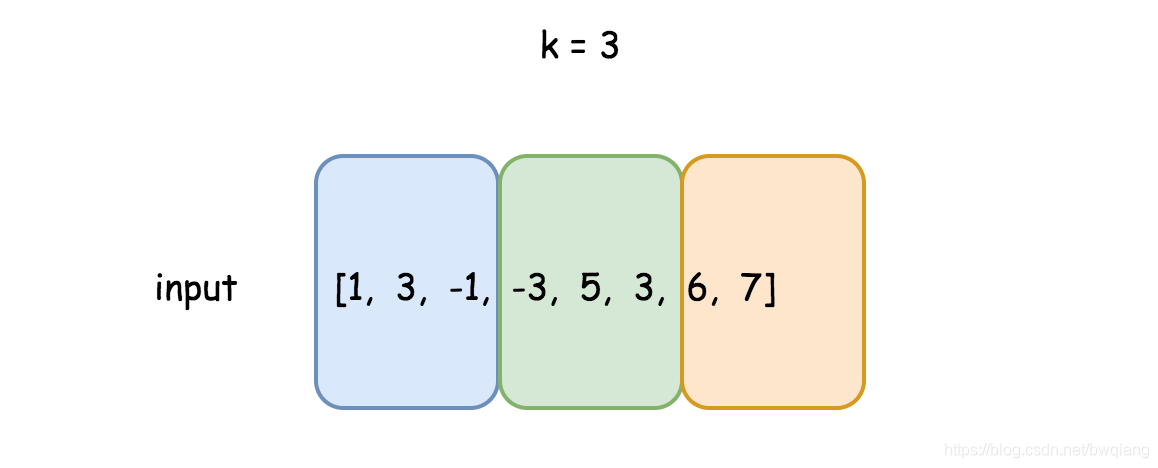
在这里插入图片描述

开头元素为 $i$ ，结尾元素为 $j$ 的当前滑动窗口可能在一个块内，也可能在两个块中。

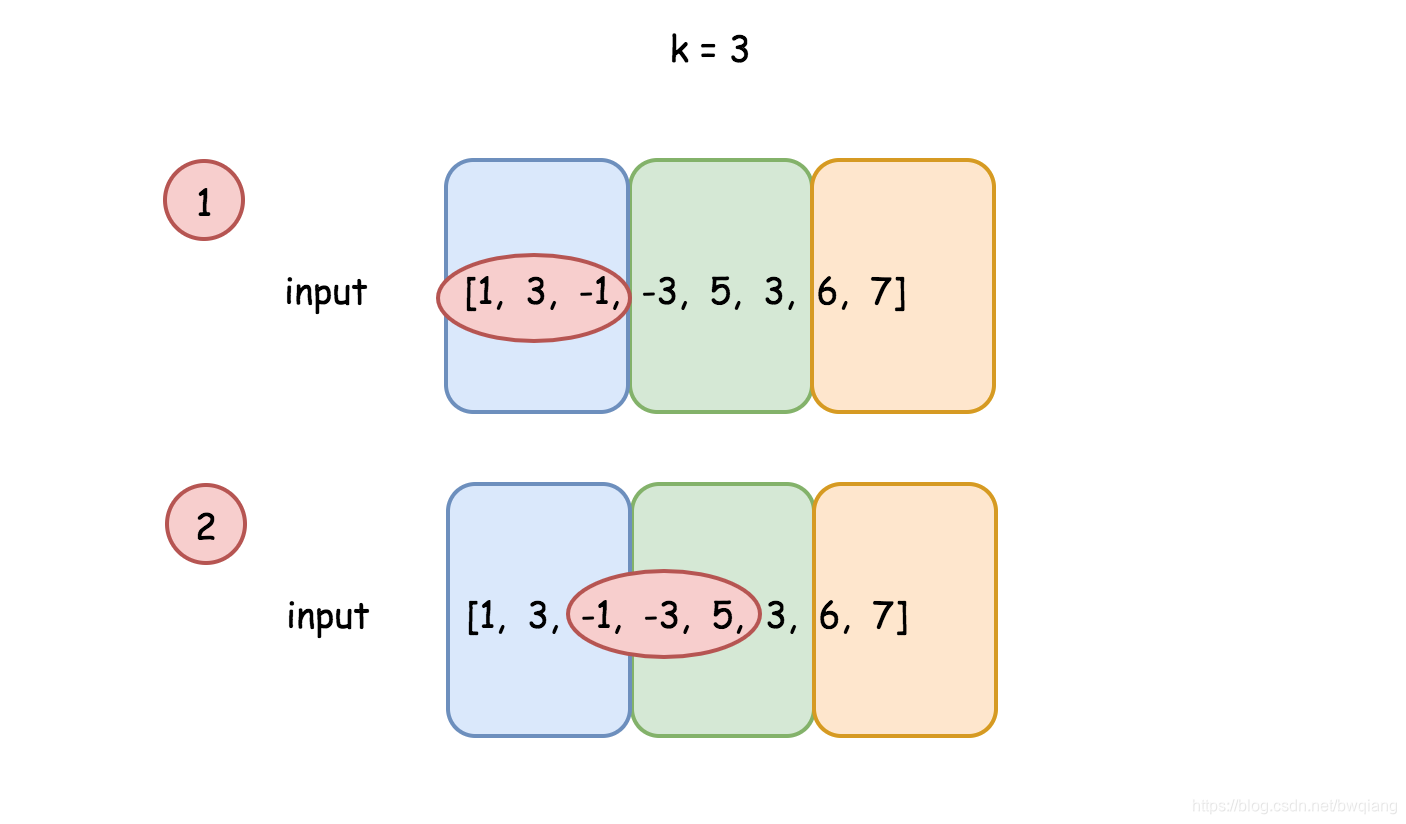
在这里插入图片描述

情况 1 比较简单。建立数组 left，其中 left[j] 是从块的开始到下标 j 最大的元素，方向左->右。

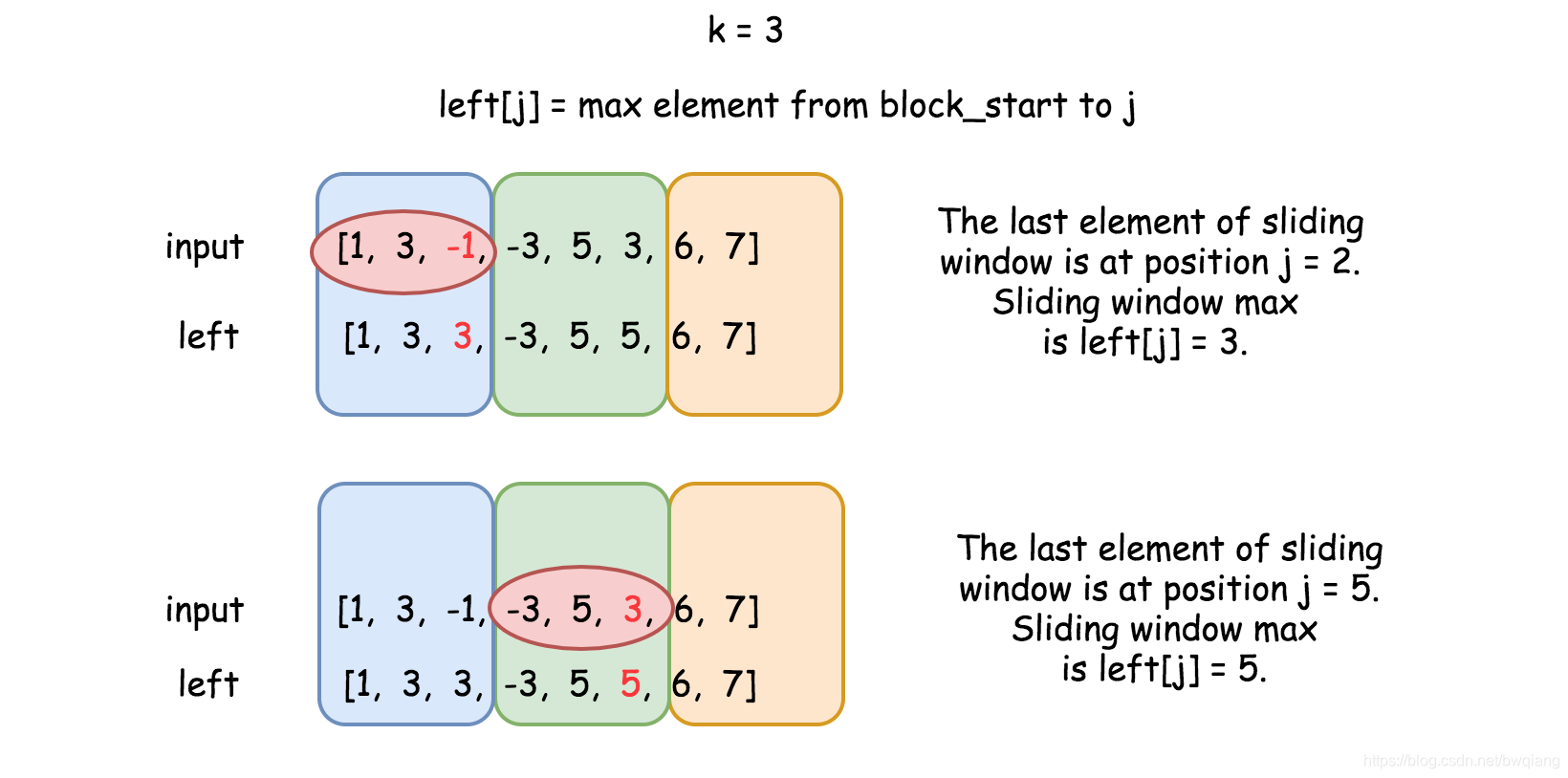
在这里插入图片描述

为了处理更复杂的情况 2，我们需要数组 right，其中 right[j] 是从块的结尾到下标 j 最大的元素，方向右->左。right 数组和 left 除了方向不同以外基本一致。

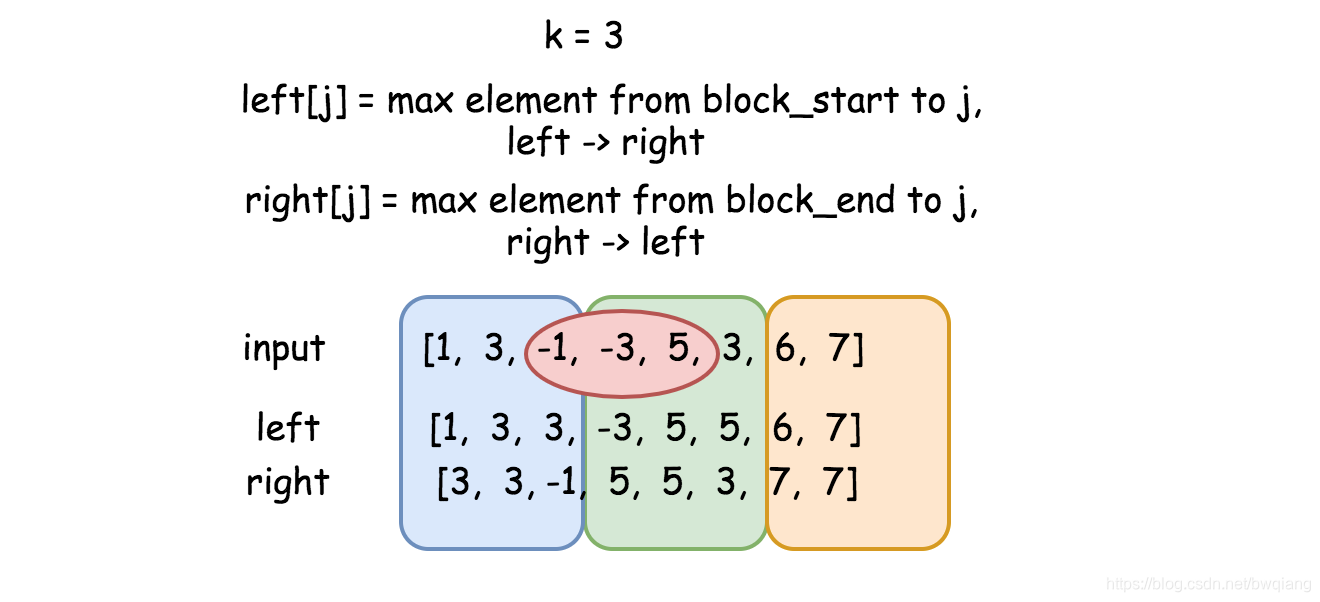
两数组一起可以提供两个块内元素的全部信息。考虑从下标 i 到下标 j的滑动窗口。根据定义，right[i] 是左侧块内的最大元素， left[j] 是右侧块内的最大元素。因此滑动窗口中的最大元素为 max(right[i], left[j])。

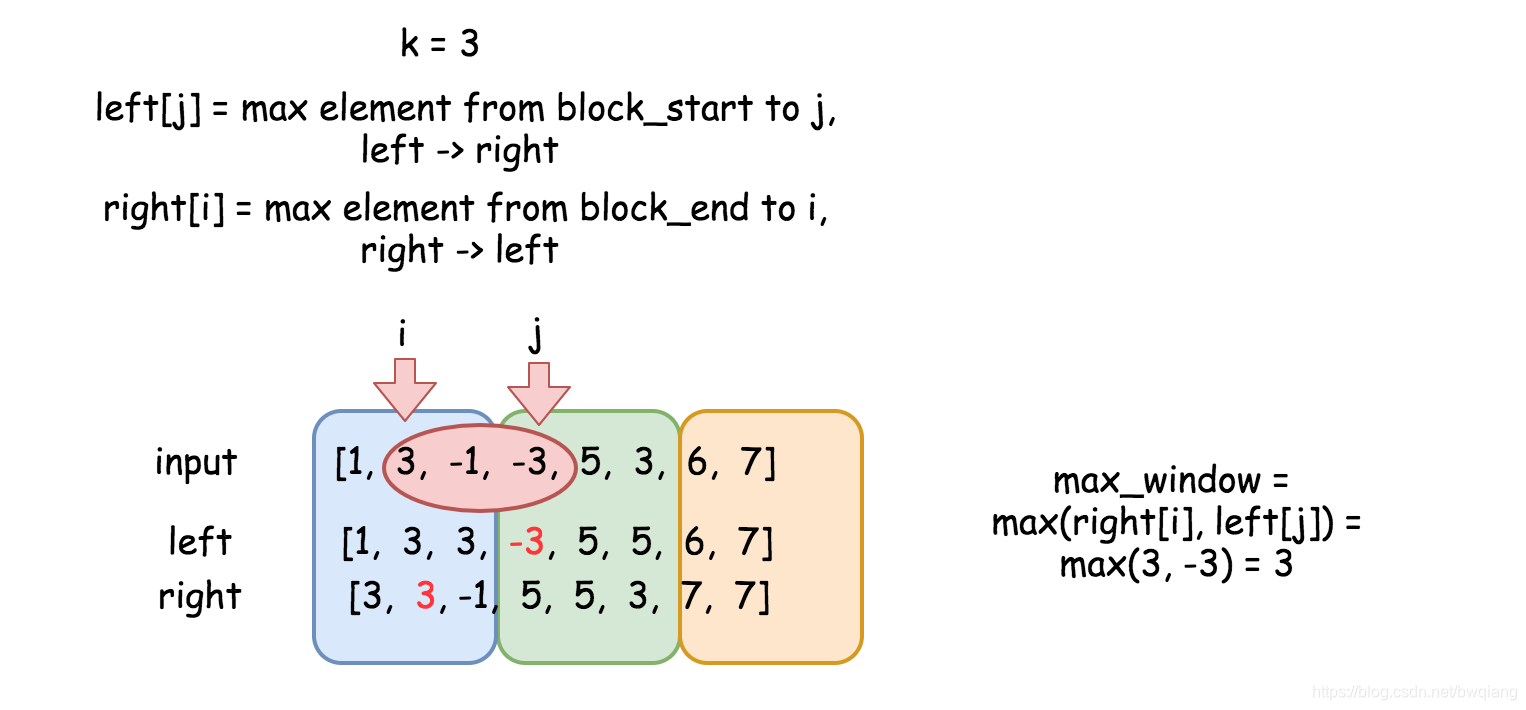
算法十分直截了当：

从左到右遍历数组，建立数组 left。
从右到左遍历数组，建立数组 right。
建立输出数组 max(right[i], left[i + k - 1])，其中 i 取值范围为 (0, n - k + 1)。

（2）

class Solution:
    def maxSlidingWindow(self, nums: 'List[int]', k: 'int') -> 'List[int]':
        n = len(nums)
        if n * k == 0:
            return []
        if k == 1:
            return nums
        
        left = [0] * n
        left[0] = nums[0]
        right = [0] * n
        right[n - 1] = nums[n - 1]
        for i in range(1, n):
            # from left to right
            if i % k == 0:
                # block start
                left[i] = nums[i]
            else:
                left[i] = max(left[i - 1], nums[i])
            # from right to left
            j = n - i - 1
            if (j + 1) % k == 0:
                # block end
                right[j] = nums[j]
            else:
                right[j] = max(right[j + 1], nums[j])
        
        output = []
        for i in range(n - k + 1):
            output.append(max(left[i + k - 1], right[i]))
            
        return output