搞定leetcode面试经典150题之二分查找

醒了就刷牙

已于 2024-12-20 16:00:58 修改

阅读量710

点赞数 21

CC 4.0 BY-SA版权

分类专栏： LeetCode刷题文章标签： leetcode 面试算法

于 2024-12-16 20:51:04 首次发布

本文链接：https://blog.youkuaiyun.com/buyaotutou/article/details/144500506

LeetCode刷题专栏收录该内容

31 篇文章

订阅专栏

系列博客目录

文章目录

系列博客目录
理论知识
例题

理论知识

二分查找（Binary Search）是一种在已排序的数组或列表中查找特定元素的高效算法，其基本思想是每次将查找范围缩小一半，从而显著减少查找时间。

基本理论：

前提条件：二分查找要求数组必须是已排序的（升序或降序都可以）。
过程：通过比较目标值与数组中间元素的大小关系，决定是继续在左半部分查找，还是继续在右半部分查找。
- 若目标值小于中间元素，则目标值只可能在中间元素的左侧。
- 若目标值大于中间元素，则目标值只可能在中间元素的右侧。
结束条件：当查找区间缩小到一个元素时，如果该元素等于目标值，则查找成功；如果该元素不等于目标值，且区间无法继续缩小，则查找失败。

算法步骤：

假设目标元素是target，数组是arr，长度是n，二分查找的算法可以分为以下几个步骤：

初始化查找区间的左右边界：left = 0，right = n - 1。
进入循环，判断当前区间是否有效：left <= right。
计算中间位置：mid = (left + right) / 2。
判断目标值与中间元素的大小：
- 若 arr[mid] == target，则查找成功，返回mid。
- 若 arr[mid] > target，则继续在左半部分查找：right = mid - 1。
- 若 arr[mid] < target，则继续在右半部分查找：left = mid + 1。
如果退出循环（查找失败），则返回未找到的标志。

二分查找的时间复杂度：

时间复杂度：O(log n)，其中n是数组的长度。每次查找都将查找区间缩小一半，因此查找的次数是对数级别的。
空间复杂度：O(1)（对于迭代实现），因为只需要常量空间存储left、right和mid等变量。

二分查找的变种：

查找第一个等于目标值的元素：如果有多个相同的元素，可以通过修改判断条件，使其找到第一个符合条件的元素。
查找最后一个等于目标值的元素：同样可以修改判断条件，找到最后一个符合条件的元素。

注意事项：

二分查找只能在已排序的数组上进行，未排序的数组需要先排序。
在实现时，特别要注意整数溢出的情况，mid可以通过mid = left + (right - left) / 2来计算，而不是直接mid = (left + right) / 2，避免因left和right很大时相加导致溢出。

模板

在这里插入图片描述

public static int findLeftEq(int[] arr, int num) {
    int l = 0;
    int r = arr.length - 1;
    int res = -1;
	int m = 0;
    while (l <= r) {
        m = l + ((r - l) >> 1); // 计算中间索引，避免溢出
        if (arr[m] == num) {
            res = m; // 找到目标值，记录位置
            r = m - 1; // 继续向左半边查找，确保找到第一个等于目标的元素
        } else if (arr[m] > num) {
            r = m - 1; // 目标值在左半边
        } else {
            l = m + 1; // 目标值在右半边
        }
    }
    return res; // 返回结果，若未找到目标值，返回 -1
}

例题

35.搜索插入位置

链接

利用下面第34题中的代码和思想，寻找大于等于target的最左边的位置。通过res来记录符合条件的坐标。给res赋初值为nums.length，正好可以如果数组中所有的值都比target小，target就应该插入到nums.length的位置。

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length -1;
        int mid = 0;
        int res = nums.length;
        while(left <= right){
            mid = left + ((right - left) >> 1);
            if(nums[mid] >= target){
                res = mid;
                right = mid - 1;//通过移动右指针，不断往左寻找更合适的下表
            }else {
                left = mid + 1;
            }
        }
        return  res;
    }
}

74.搜索二维矩阵

链接
思路：对二维矩阵第一维进行二分查找，我们只在移动左指针时候更新存储target所在行的res。因为右指针肯定不对，其第0个元素都比target大，那后面元素肯定更大。我们不断更新res，到了最后一次在左指针更新res的时候，我们通过res保存了左指针，之后左指针变化但是没有找到target，也就是说如果后面找不到matrix[mid][0] == target，它只可能在第res行(left的上一次所指向的行)中。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int right = matrix.length - 1;
        int left = 0;
        int mid = 0;
        int res = 0;
        while(left <= right){
            mid = left + ((right - left) >> 1);
            if(matrix[mid][0] == target){
                res = mid;
                return true;
            } else if (matrix[mid][0] < target) {
                res = mid;
                //因为target只能存在matrix[mid][0] < target所在的第m行中，我们不断更新res
                //如果之后没有找到target（matrix[mid][0] == target），也就是说其在res所存的第m行中，其右边没有比这更可能满足的情况。
                left = mid + 1;//注意上面已经保存了mid，这时候left=mid+1，而不是left = mid；不要想着此时的mid可能就符合最后的res，就不舍得left跳过他，他已经被res保存，不会错过。
            }else {
                right = mid - 1;
            }
        }
        int[] line = matrix[res];
        left = 0;
        right = line.length - 1;
        mid = 0;
        while(left <= right){
            mid = left + ((right - left) >> 1);
            if(line[mid] == target) return true;
            else if(line[mid] < target){
                left = mid +1;
            }else {
                right = mid - 1;
            }
        }
        return false;
    }
}

162.寻找峰值

链接
写下面的代码需要先定好compare是如何比较的，比如是拿第一个参数和第二个参数比大小，第一个大就输出>0(两个参数相减)。再对后面的三位运算符进行编程。

class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        int idx = (int)(Math.random()*n);
        while(!(compare(nums, idx - 1 ,idx) < 0 &&compare(nums, idx, idx + 1) > 0)){
            if(compare(nums, idx-1, idx)>0){
                idx --;
            }else {
                idx ++;
            }
        }
        return idx;
    }
    public int[] get(int[] nums, int idx){
        if(idx == -1 || idx == nums.length){
            return new int[]{0,0};
        }
        return new int[]{1,nums[idx]};
    }
    public int compare(int[] nums, int idx1, int idx2){
        int[] num1 = get(nums, idx1);
        int[] num2 = get(nums, idx2);
        if(num1[0] != num2[0]){
            return num1[0] < num2[0] ? -1 : 1;
        }
        if (num1[1] == num2[1]) return 0; //这行代码可以去掉
        else return num1[1] > num2[1] ? 1 : -1;
    }
}

加入二分查找后，达到时间复杂度要求

class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        int left = 0, right = n - 1, ans = -1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (compare(nums, mid - 1, mid) < 0 && compare(nums, mid, mid + 1) > 0) {
                ans = mid;
                break;
            }
            if (compare(nums, mid, mid + 1) < 0) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return ans;
    }

    // 辅助函数，输入下标 i，返回一个二元组 (0/1, nums[i])
    // 方便处理 nums[-1] 以及 nums[n] 的边界情况
    public int[] get(int[] nums, int idx) {
        if (idx == -1 || idx == nums.length) {
            return new int[]{0, 0};
        }
        return new int[]{1, nums[idx]};
    }

    public int compare(int[] nums, int idx1, int idx2) {
        int[] num1 = get(nums, idx1);
        int[] num2 = get(nums, idx2);
        if (num1[0] != num2[0]) {
            return num1[0] > num2[0] ? 1 : -1;
        }
        if (num1[1] == num2[1]) {//这个if判断可以去掉
            return 0;
        }
        return num1[1] > num2[1] ? 1 : -1;
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/find-peak-element/solutions/998152/xun-zhao-feng-zhi-by-leetcode-solution-96sj/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

33.搜索旋转排序数组

链接
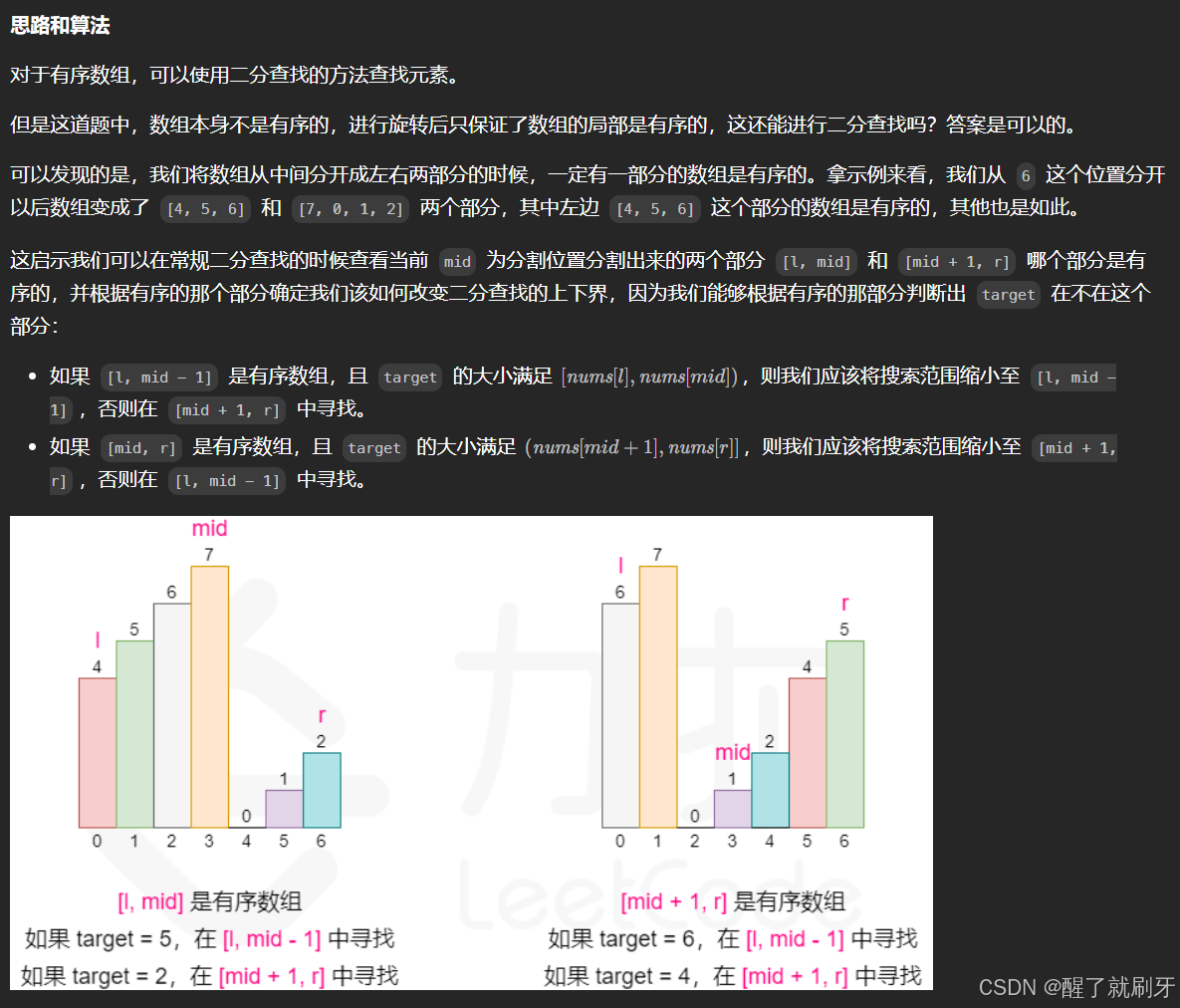
在这里插入图片描述
数组经过旋转后，变成了两部分，如果nums[mid]它大于nums[nums.length-1],说明mid在左部分，如果target也在mid左边的话我们就可以把right指针移动(过来到mid左边)，现在left指针和right指针都在左部分了，再在左部分(现在left指针和right指针中的值递增了）中利用二分查找。如果target不在，那就只能把left指针移动到mid左边，这时候可能left指针与right指针中间还是有两部分序列，并不严格递增，再进行下一次判断。

class Solution {
    public int search(int[] nums, int target) {
        int right = nums.length - 1;
        int left = 0;
        while(left <= right){
            int mid = left + ((right - left) >> 1);
            if(nums[mid] == target){
                return mid;
            } else if (nums[mid] < nums[right]) {
                if(nums[mid] < target && nums[right] >= target){
                    left = mid +1;
                }else {
                    right = mid -1;
                }
            }
            else {
                if(nums[mid] > target && target >= nums[left]){
                    right = mid -1;
                }else {
                    left =mid +1;
                }
            }
        }
        return -1;
    }
}

34.在排序数组中查找元素的第一个和最后一个位置

链接
比如target为8，我们要找到大于等于8的最左边的位置和小于等于8的最右边的位置。注意不一定有target存在于数组中。
在这里插入图片描述

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums.length == 0){
            return new int[]{-1, -1};
        }
        int left = 0;
        int right = nums.length - 1;
        int mid = 0;
        int res = -1;
        while(left<=right){
            mid = left + ((right - left) >> 2);
            if(nums[mid] == target){//满足大于等于target，保存位置，用于后续判定
                res = mid;
                right = mid - 1;
            } else if (nums[mid] > target) {//满足大于等于target，保存位置，用于后续判定
                res = mid;
                right = mid - 1;
            }else {
                left = mid + 1;
            }
        }
        int res_left = res;
        left = 0;
        right = nums.length - 1;
        mid = 0;
        res = -1;
        while(left<=right){
            mid = left + ((right - left) >> 2);
            if(nums[mid] == target){
                res = mid;
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            }else {
                res = mid;
                left = mid + 1;
            }
        }
        int res_right = res;
        if(res_left <= res_right && res_right != -1&& res_left != -1 && nums[res_left] == target && nums[res_right] == target ){
            return new int[]{res_left, res_right};
        }

        return new int[]{-1, -1};
    }
}

153.寻找旋转排序数组中的最小值

链接
根据上题的思路，我们现在是要找比nums[mid]小的值，但与之前存在不同。我们还是认为此时数组由两个递增的部分组成，也就是说如果当前位置的值，比右指针小，那当前位置和右指针都在同一部分，而又因为当前比右指针小，所以右指针可以移动到当前节点，右指针移动过程中略过的中间节点都是比当前节点大的。如果当前节点比右指针大，那说明不在同一部分，左指针应该移动到mid的右边，移动所经过的点的值都比当前右指针大，而且mid也比右指针大，所以应该移动到mid右边。
这时候如果左右指针指向同一位置，则说明找到了。
在这里插入图片描述

class Solution {
    public int findMin(int[] nums) {
        int right = nums.length - 1;
        int left = 0;
        while(left<right){
            int mid = left + ((right - left) >> 1);
            if(nums[mid] < nums[right]){//说明nums[mid]可能是最小值
                right = mid;
            }else {
                left = mid + 1;//此时mid肯定不是最小值，所以left = mid + 1，因为nums[mid]>nums[right] 注意数组nums中无重复数值
            }
        }
        return nums[left];
    }
}