搞定leetcode面试经典150题之矩阵

系列博客目录

---

---

理论知识

二维数组的别名就是矩阵，如果说数组是最简单的数据结构的话， 矩阵就是它的扩展，当数据的结构关系使用单一的维度无法承载的时候，我们就尝试利用矩阵进行处理，矩阵就是二维数组，用多一级的索引将数组组织起来。

例题

73. 矩阵置零 中等

相关标签：数组、矩阵、原地算法

问题描述：
给定一个 m x n 的矩阵，如果其中有一个元素为 0 ，则将其所在的行和列的所有元素都设为 0 。要求使用原地算法，即不使用额外的矩阵空间。

示例：

示例 1

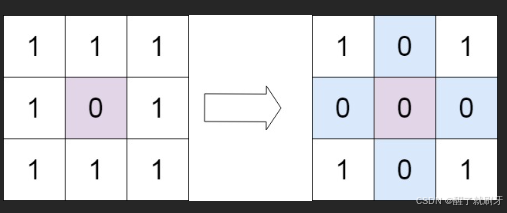
输入：

matrix = [[1,1,1],[1,0,1],[1,1,1]]

输出：

[[1,0,1],[0,0,0],[1,0,1]]

示例 2

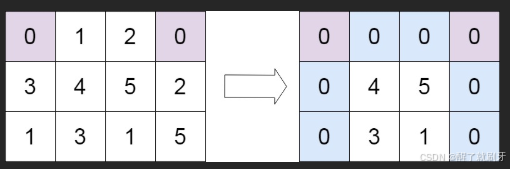
输入：

matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]

输出：

[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -2^31 <= matrix[i][j] <= 2^31 - 1

题解

思路：我们可以用第一行和第一列的空间用来做标记，处理完毕除了第一行第一列外其他矩阵的内容后，也需要判断是否最后要把第一行第一列置零。

注意：两个双重for循环都要从1开始遍历
0ms击败100.00%

class Solution {
   
   
    public void setZeroes(int[][] matrix) {
   
   
        int m = matrix.length;
        int n = matrix[0].length;
        boolean rowOfFirst = false;
        boolean colOfFirst = false;
        for (int i = 0; i < m; i++) {
   
   
            if(matrix[i][0] == 0){
   
   
                colOfFirst = true;//行和列不要搞错
            }
        }
        for (int i = 0; i <n; i++) {
   
   
            if(matrix[0][i] == 0){
   
   
                rowOfFirst = true;
            }
        }
        for (int i = 1; i < m; i++) {
   
   
            for (int j = 1; j < n; j++) {
   
   //这个和下面的两个双重for循环都要从1开始遍历
                if(matrix[i][j] == 0){
   
   
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; i++) {
   
   
            for (int j = 1; j < n; j++) {
   
   
                if(matrix[i][0] == 0 || matrix[0][j] == 0){
   
   
                    matrix[i][j] = 0;
                }
            }
        }
        if(colOfFirst){
   
   
            for (int i = 0; i < m; i++) {
   
   
                matrix[i][0] = 0;
            }
        }
        if(rowOfFirst){
   
   
            for (int i = 0; i < n; i++) {
   
   
                matrix[0][i] = 0;
            }
        }
    }
}

54. 螺旋矩阵 中等

相关标签：数组、矩阵、模拟

问题描述：
给定一个 m 行 n 列的矩阵 matrix，请按照顺时针的螺旋顺序，返回矩阵中的所有元素。

示例 1

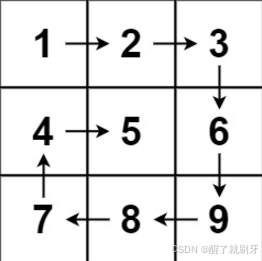
输入：

matrix = [[1,2,3],[4,5,6],[7,8,9]]

输出：

[1,2,3,6,9,8,7,4,5]

示例 2

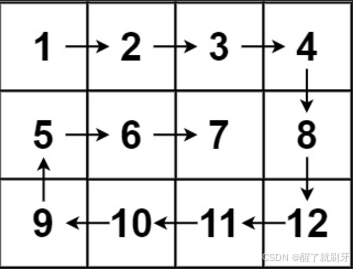
输入：

matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]

输出：

[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

• m == matrix.length