3月31日毕设准备

3月31日毕设准备

毕业设计需要深度和工作量，深度方面我准备仔细钻研一下深度学习的基础数学知识。通过观看吴恩达的视频。
P31 5-6矢量

这里我们主要理解上面的非适量表达方式以及下面的矢量化后的表达方式。
并且理解他们两个实际上是等价的。向量化效率更高。
P32 6-1分类
接下来几个part会讨论y离散情况下的分类问题，设计一个logistics回归算法。

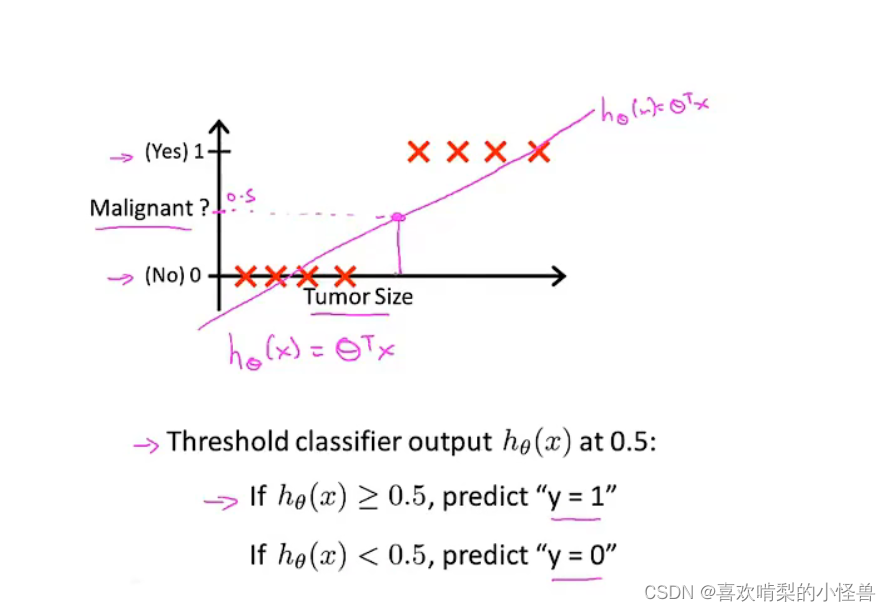
将x轴延长一下，加入一个样本。你运行线性回归，你会得到另外一条线去拟合data。

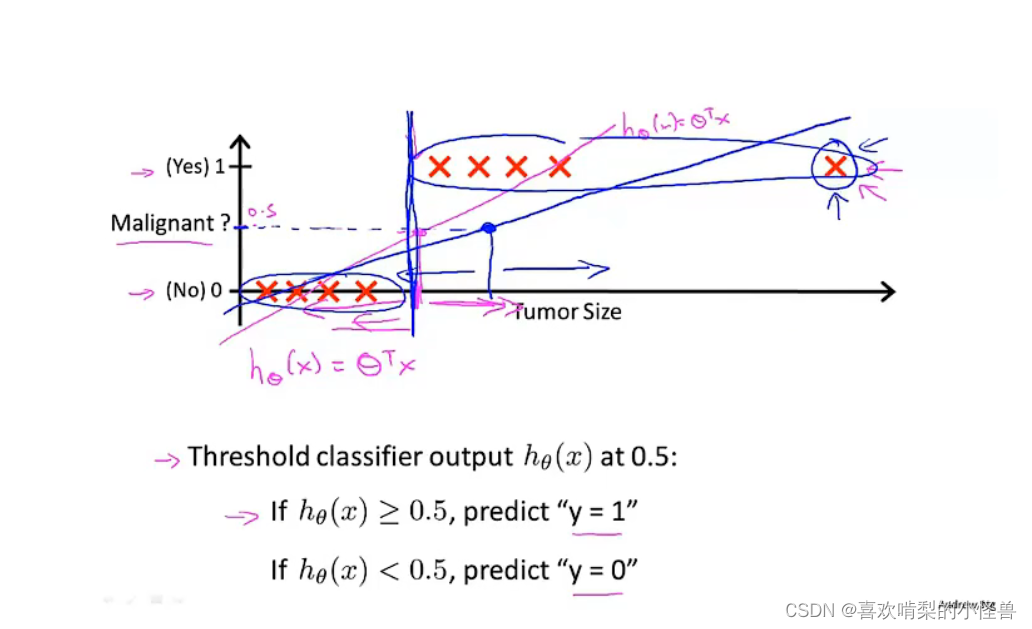
这是一个差劲的线性回归，有些没有分类正确。新增加的例子没有新的信息，本来的线性回归也可以正确分类，但是加入以后，无法正确分类其他的样本了。所以不推荐线性回归用在分类中问题。

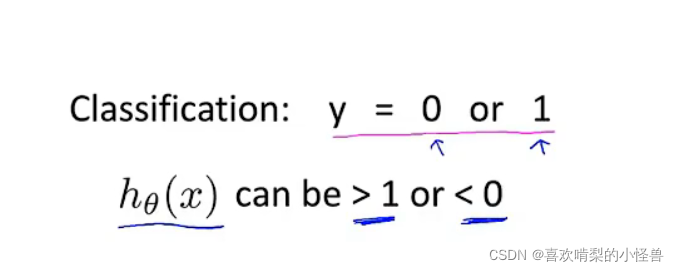
我们在样本都为0或1时，用线性回归会产生结果为大于1或者小于零的情况，我们理应知道这样时肯定不合理的。所以我们用logistic回归的算法。

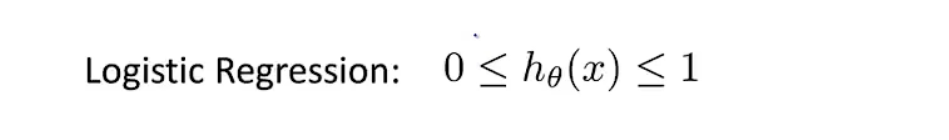
其特点在于算法的输出值或者叫预测值一直介于0和1之间。
逻辑回归算法因为带有“回归”二字（因为历史原因），会令人误解，其实逻辑回归算法是一种分类算法。
P33 6-2假设陈述
当有一个分类问题时，我们应该采用哪个方程来表示我们的假设。
因为我们想要让预测值介于1和0之间，所以我们提出一个假设来满足这些性质。

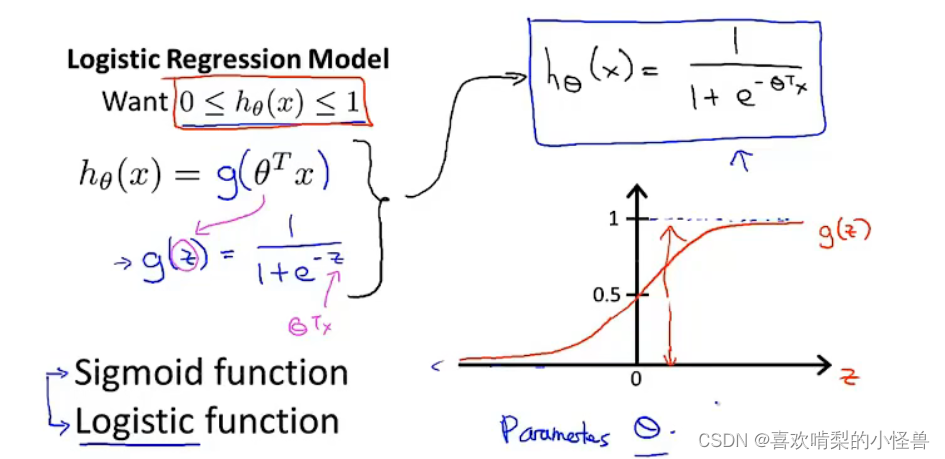
我们叫g(z)为逻辑函数（逻辑回归算法名字的来源）或sigmoid function。
有了假设函数hθ(x),我们要做的和之前一样，用参数θ 拟合我们的数据

hθ(x)表示对于一个输入x，y=1的概论估计；
 hθ(x) = P(y=1|x;θ) “在给定x的条件下y=1的概率”
 6.3 决策边界
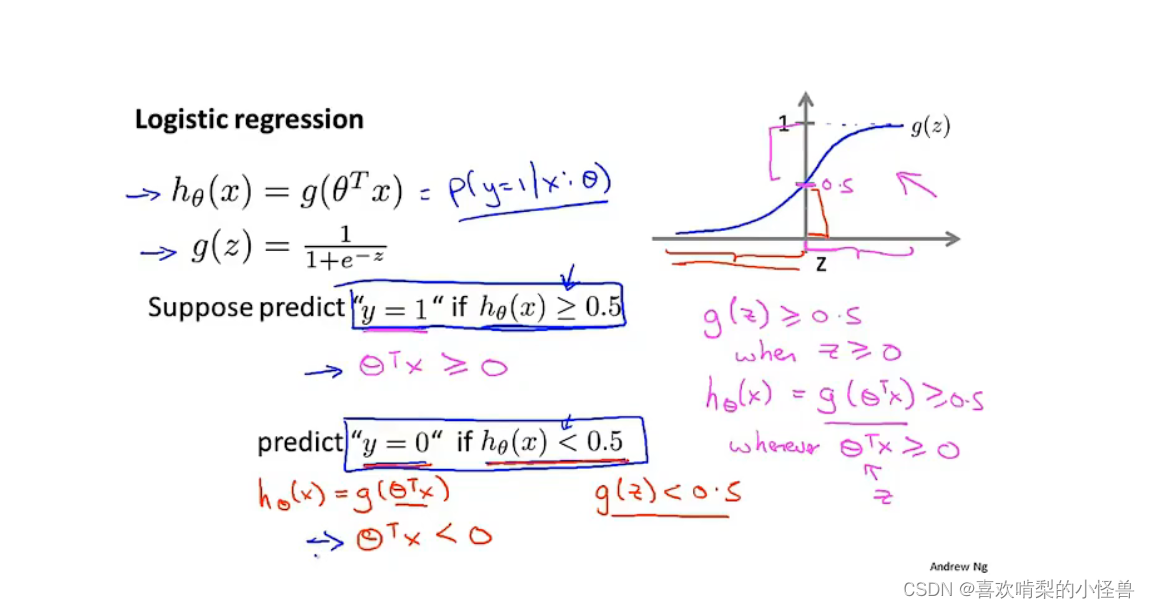 上图中果我们要决定预测y=1还是y=0，取决于估值概率P(y=1|x;θ)是大于等于0.5还是小于0.5，这就是说我们将预测y=1，只需要θTx大于或等于0，另一方面我们将预测y=0，只需要θTx小于0

假设有一个训练集的假设函数是hθ(x) = g(θ0+θ1x1+θ2x2)，设已经拟合好了参数，θ0=-3，θ1=1，θ2=1，其决策边界如下：
  
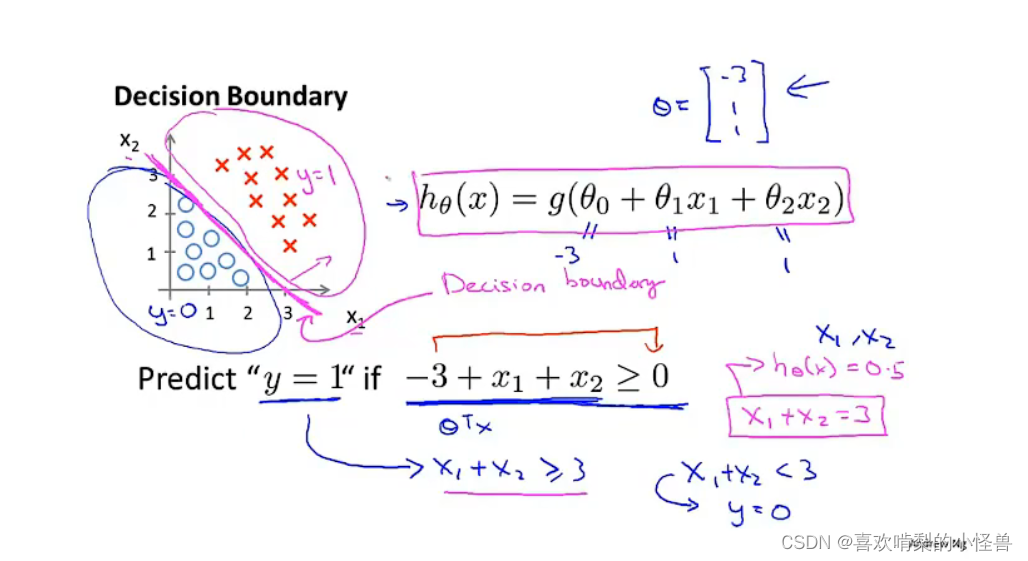
图中紫色直线为决策边界，上面y=1，下面y=0，需要注意的是，去掉数据后，这条决策边界以及y=0和y=1的区域依然存在，他们都是假设函数的属性。后面我们将用数据来确定θ_0，θ_1,θ_2,但是一旦确定好这三个参数，我们就将完全确定决策边界。

上面是两个更复杂通过确定好参数后形成的决策边界。
6-4 代价函数
如何拟合logistics回归中的模型参数θ
在这段视频中，我们要介绍如何拟合逻辑回归模型的参数θ \thetaθ。具体来说，我要定义用来拟合参数的优化目标或者叫代价函数，这便是监督学习问题中的逻辑回归模型的拟合问题。

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于

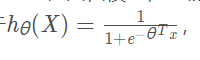
当我们将带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。


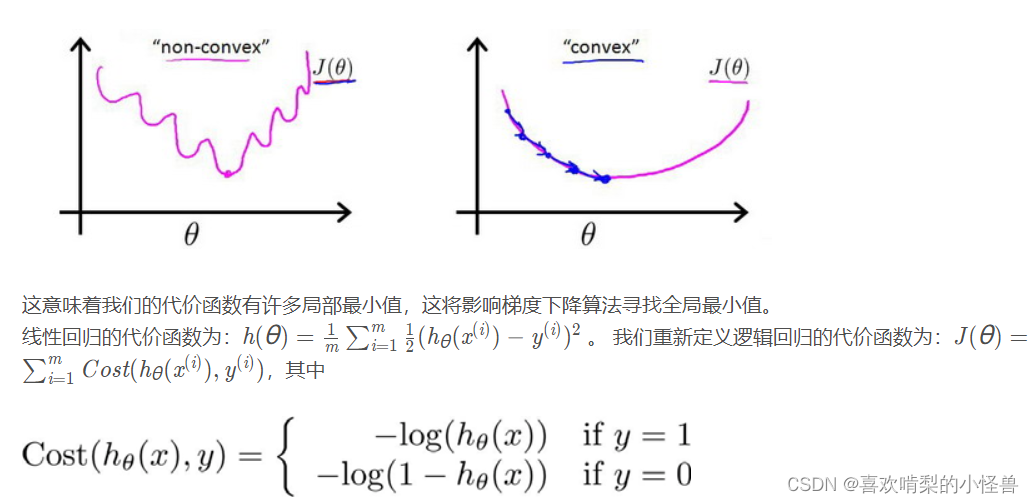
6-5 简化代价函数与梯度下降
这种costfunction时由极大似然法得出。
需最小化新的cost function

最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

首先我们来看看Logistic回归的代价函数：

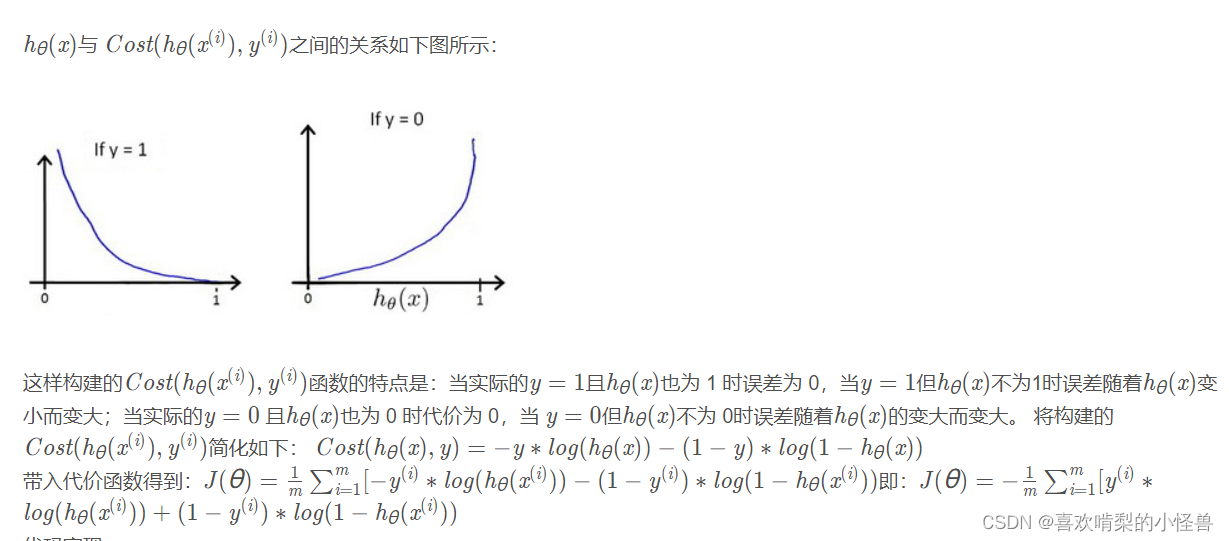
上面y=1和y=0的代价函数是不同的表达式，我们将其化简合并为同一个表达式：

约定y只能取0或1，可以将cost的两种情况合并为一种，将二者分别乘一个系数再相加，以令y取一个值时，另一项则为0.

化简后的代价函数：

我们再化简梯度下降算法：


使用梯度下降法，求偏导数。
结果看似与线性回归相同，但是由于h变成了sigmoid函数，所欲实质不同。

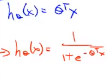
线性回归的假设函数是蓝色的表达式，Logistic回归的假设函数是红色的表达式
6-7多元分类：一对多

把三角形当成‘正’类别，把正方形当成‘正’类别，把星型当成‘正’类别，拟合出三个分类器。
我们要预测新的x时，对三个分类器都输入x，然后选择h最大的类别，得到的最大h对应的y就是我们需要的值。