算法：leetcode_129_求根节点到叶节点数字之和

目录

0. 前言

1. 题目介绍

2. 思路

2.1 设置重要变量

2.1.1 路径：path

2.1.2 返回结果：result

2.2 递归思路

2.2.1 更新路径变量

 2.2.2 何时更新结果result变量

 2.2.3 回溯最重要的一步

2.2.4 换儿子

 2.2.5 回归父母

2.2.6 继续递归

2.2.7 代码

 3. 代码

Java：

 C++：

JS：

Python：

---

0. 前言

这是字节面试的一道题目

129. 求根节点到叶节点数字之和 - 力扣（LeetCode）

在CodeTop第四页, 属于频率不是很高的一道面试题。

CodeTop是各个公司按照频率进行排序的leetcode算法合集, 特别适合找工作面试。

CodeTop 面试题目总结

1. 题目介绍

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

计算从根节点到叶节点生成的 所有数字之和 。

示例 ：

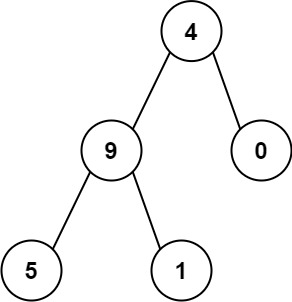
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495从根到叶子节点路径 4->9->1 代表数字 491从根到叶子节点路径 4->0 代表数字 40因此，数字总和 = 495 + 491 + 40 = 1026

2. 思路

很明显这是一道经典的递归、回溯题，甚至是模板题。

2.1 设置重要变量

回溯模板题 直接无脑设置两个变量：

2.1.1 路径：path

根据类型设置不同的路径类型, 题目需要的是字符串就设置个StringBuilder(电话号码的字母组合)，需要一个路径链路或者组合(组合总和 II)就设置成LinkedList。

需要数字就设置int类型, 即本题。

2.1.2 返回结果：result

根据个人习惯， 我喜欢设置成静态类型，懒得在函数里面传递参数，并且递归函数无需返回值。

2.2 递归思路

这道题的递归无需传递深度，开始索引等，因此就传递一个树类型的参数即可。

由于将需要的重要变量设置为了静态类型，因此无需返回值：

public static void dfs(TreeNode root)

递归方向可以选择：

根->左->右(中序)

根->右->左 均可

即在这个节点处理完之后, dfs(左儿子)，然后dfs(右儿子)。

一般都考虑中序遍历，习惯了。

2.2.1 更新路径变量

对于整数的拼接，当然是位数增多并且加上新的个位数。

path = path * 10 + root.val;

2.2.2 何时更新结果result变量

很明显当然是本次递归走到了尽头，即当前访问的节点是叶子节点，无儿无女节点。

if (root.left == null && root.right == null)

走到了尽头，返回去之前记得带上你本轮的战利品，把你的path带走。

此时result会加上当前的一串数值，比如示例中的495。

result += path;

2.2.3 回溯最重要的一步

回溯回溯，为什么叫回溯，悬崖勒马，走到了节点尽头，我要返回去一步， return!

这是数值类型的路径变量，直接除了十，去掉个位数即可。

如果是LinkedList或者StringBuilder类型的path， 直接去除最后一个元素即可。

path /= 10;
return;

此时，对于示例的第一步，将左下角的叶子节点“5”扔掉，回到了他爹节点"9"。

此时的path为49。

2.2.4 换儿子

当前的根节点"9"的左儿子"5"已经访问完了，接下来dfs()它的另一个孩子节点"1"。

path再拼接上"1"，变为"491"。

path = path * 10 + root.val;

2.2.5 回归父母

此时又遇到了2.2.3 这一步, "1"为叶子节点, 处理完之后就要return。

返回之后, 即它的父节点"9"已经完成了它的任务，将左右节点"5"和"1"都处理完了。

"9"也要回归它的父节点"4", 即此时path还要除以10；

path /= 10;

2.2.6 继续递归

继续递归，知道遍历完整棵树的相对最右下角的节点（根->左->右），当然不是所有节点都是有右孩子节点的，因此是相对最右下角。

2.2.7 代码

/**
 * @author: Rehse
 * @description: 求根节点到叶节点数字之和
 * @date: 2025/7/29
 */
public class Leetcode_129_SumRootToLeafNumbers {
    // 定义路径变量
    public static int path;
    // 定义返回结果
    public static int result;

    public static int sumNumbers(TreeNode root) {
        // 赋初值
        path = 0;
        result = 0;
        // 从根节点开始dfs
        dfs(root);
        return result;
    }

    public static void dfs(TreeNode root) {
        // 更新路径变量
        path = path * 10 + root.val;
        if (root.left == null && root.right == null) {
            // 带上这一轮的战利品 放进结果变量里面
            result += path;
            // 叶子节点处理完毕 回溯
            path /= 10;
            // 可以每一轮都打印出路径和结果变量, 方便排查问题
            // System.out.println("path : " + path);
            // System.out.println("result : " + result);
            return;
        }
        // 递归访问左孩子节点
        dfs(root.left);
        // 递归访问右孩子节点
        dfs(root.right);
        // 两个孩子都访问完毕 回溯
        path /= 10;
    }

    public static void main(String[] args) {
        // 构建打印树工具
        PrintUtils utils = new PrintUtils(new int[]{4, 9, 0, 5, 1}, 1);
        // 打印出树结构
        utils.print();
        // 获取树结构 放进此题的核心函数内
        TreeNode root = utils.getTreeNode();
        int res = sumNumbers(root);
        System.out.println(res);
    }
}

运行下：

这里的打印树结构的工具我有在另一篇文章分享：打印节点(链表或者二叉树)工具-优快云博客

跟示例一样，提交吧。

啊啊啊错啦！

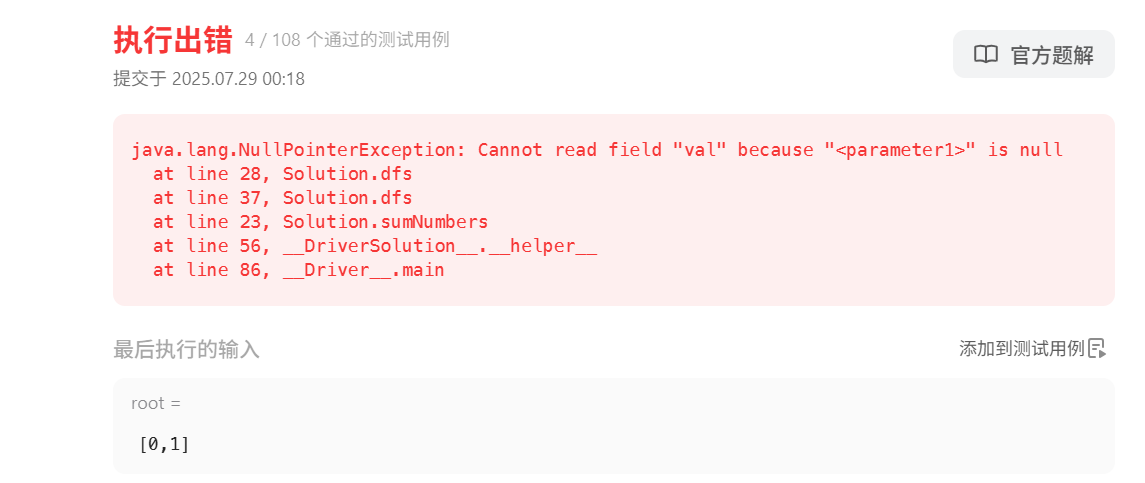
打印出树结构：这棵树比较简单，复杂的树打印出来效果更明显。

PrintUtils utils1 = new PrintUtils(new int[]{0, 1}, 1);
utils1.print();

树的结构是这样的：

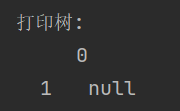
哦哦哦，当处理完左孩子节点"1"之后，开始dfs(右孩子"null")

此时进入dfs的更新路径变量这一步：

path = path * 10 + root.val;

它都是空的，哪儿来的val, 因此空指针异常。

我们直接在dfs()函数的第一步就加上判断条件，空节点直接返回。

if(root == null) return ;

再次提交：过啦！

3. 代码

Java：

/**
 * @author: Rehse
 * @description: 求根节点到叶节点数字之和
 * @date: 2025/7/29
 */
public class Leetcode_129_SumRootToLeafNumbers {
    // 定义路径变量
    public static int path;
    // 定义返回结果
    public static int result;

    public static int sumNumbers(TreeNode root) {
        // 赋初值
        path = 0;
        result = 0;
        // 从根节点开始dfs
        dfs(root);
        return result;
    }

    public static void dfs(TreeNode root) {
        // 空节点直接返回
        if(root == null) return ;
        // 更新路径变量
        path = path * 10 + root.val;
        if (root.left == null && root.right == null) {
            // 带上这一轮的战利品 放进结果变量里面
            result += path;
            // 叶子节点处理完毕 回溯
            path /= 10;
            // 可以每一轮都打印出路径和结果变量, 方便排查问题
            // System.out.println("path : " + path);
            // System.out.println("result : " + result);
            return;
        }
        // 递归访问左孩子节点
        dfs(root.left);
        // 递归访问右孩子节点
        dfs(root.right);
        // 两个孩子都访问完毕 回溯
        path /= 10;
    }

    public static void main(String[] args) {
        // 构建打印树工具
        PrintUtils utils = new PrintUtils(new int[]{4, 9, 0, 5, 1}, 1);
        // 打印出树结构
        utils.print();
        // 获取树结构 放进此题的核心函数内
        TreeNode root = utils.getTreeNode();
        int res = sumNumbers(root);
        System.out.println(res);


        PrintUtils utils1 = new PrintUtils(new int[]{0, 1}, 1);
        utils1.print();

    }
}

C++：

// 定义路径变量
int path;
// 定义返回结果
int result;

int sumNumbers(TreeNode* root) {
    // 赋初值
    path = 0;
    result = 0;
    // 从根节点开始dfs
    dfs(root);
    return result;
}

void dfs(TreeNode* root) {
    // 空节点直接返回
    if(root == nullptr) return ;
    // 更新路径变量
    path = path * 10 + root->val;
    if (root->left == nullptr && root->right == nullptr) {
        // 带上这一轮的战利品 放进结果变量里面
        result += path;
        // 叶子节点处理完毕 回溯
        path /= 10;
        // 可以每一轮都打印出路径和结果变量, 方便排查问题
        // cout << "path : " << path << endl;
        // cout << "result : " << result << endl;
        return;
    }
    // 递归访问左孩子节点
    dfs(root->left);
    // 递归访问右孩子节点
    dfs(root->right);
    // 两个孩子都访问完毕 回溯
    path /= 10;
}

JS：

// 定义路径变量
let path;
// 定义返回结果
let result;

function sumNumbers(root) {
    // 赋初值
    path = 0;
    result = 0;
    // 从根节点开始dfs
    dfs(root);
    return result;
}

function dfs(root) {
    // 空节点直接返回
    if(root == null) return ;
    // 更新路径变量
    path = path * 10 + root.val;
    if (root.left == null && root.right == null) {
        // 带上这一轮的战利品 放进结果变量里面
        result += path;
        // 叶子节点处理完毕 回溯
        path = Math.floor(path / 10);
        // 可以每一轮都打印出路径和结果变量, 方便排查问题
        // console.log("path : " + path);
        // console.log("result : " + result);
        return;
    }
    // 递归访问左孩子节点
    dfs(root.left);
    // 递归访问右孩子节点
    dfs(root.right);
    // 两个孩子都访问完毕 回溯
    path = Math.floor(path / 10);
}

Python：

# 定义路径变量
path = 0
# 定义返回结果
result = 0

def sumNumbers(root):
    global path, result
    # 赋初值
    path = 0
    result = 0
    # 从根节点开始dfs
    dfs(root)
    return result

def dfs(root):
    global path, result
    # 空节点直接返回
    if root is None:
        return
    # 更新路径变量
    path = path * 10 + root.val
    if root.left is None and root.right is None:
        # 带上这一轮的战利品 放进结果变量里面
        result += path
        # 叶子节点处理完毕 回溯
        path //= 10
        # 可以每一轮都打印出路径和结果变量, 方便排查问题
        # print("path :", path)
        # print("result :", result)
        return
    # 递归访问左孩子节点
    dfs(root.left)
    # 递归访问右孩子节点
    dfs(root.right)
    # 两个孩子都访问完毕 回溯
    path //= 10

故意在代码留点马脚，使得提交报错，可以很好帮助理解各种情况。

做题基本上很难一次就考虑到所有情况，刚把得！

觉得我的屎山代码有用的话，点个赞么么哒！

25届Java小登刚入职不久，每天回家继续提升自己能力，长期坚持终有成效，

每次写完博客，都是半夜一两点，过几秒就看到好几百访问量，希望半夜努力的你一定能够变成更完美的自己！晚安好梦~~