【Leetcode】拆分详解 - 环形链表

前言

文章细分了各个知识点，可在目录中快速跳转。
手机端用户在查看代码块时建议点击代码右上角放大查看，每一段代码均有完整注释。

本文讲解链表中的带环问题。

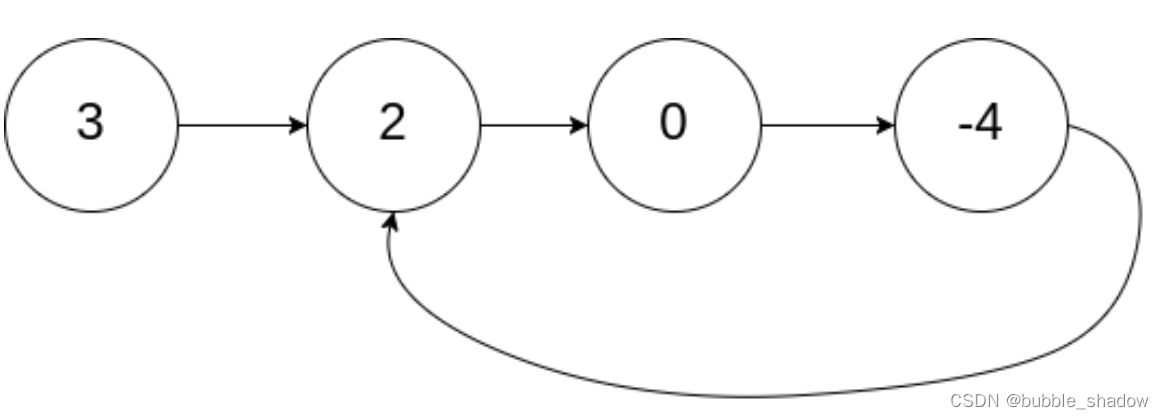
一、什么是环形链表？

1. 链表的尾节点内的指针可指向链表中的任意节点（包括它自己）
2. 无限循环，不终止

二、例题拆解

  1. 判断是否带环

• 题目描述
  
• 思路讲解

快慢指针法 - 追及问题
fast一次走两步，slow一次走一步。让fast遍历链表，如果fast能找到NULL说明不带环，如果fast追上slow（fast == slow）说明带环。

• 代码实现

bool hasCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;
    //循环结束条件既可以让fast遍历链表，也满足空节点和一个节点的特殊情况
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        
        if(fast == slow)
            return true;
    }
    return false;
}

  2. 返回环的入口点

• 题目描述
  
• 思路讲解

1. 判断是否带环
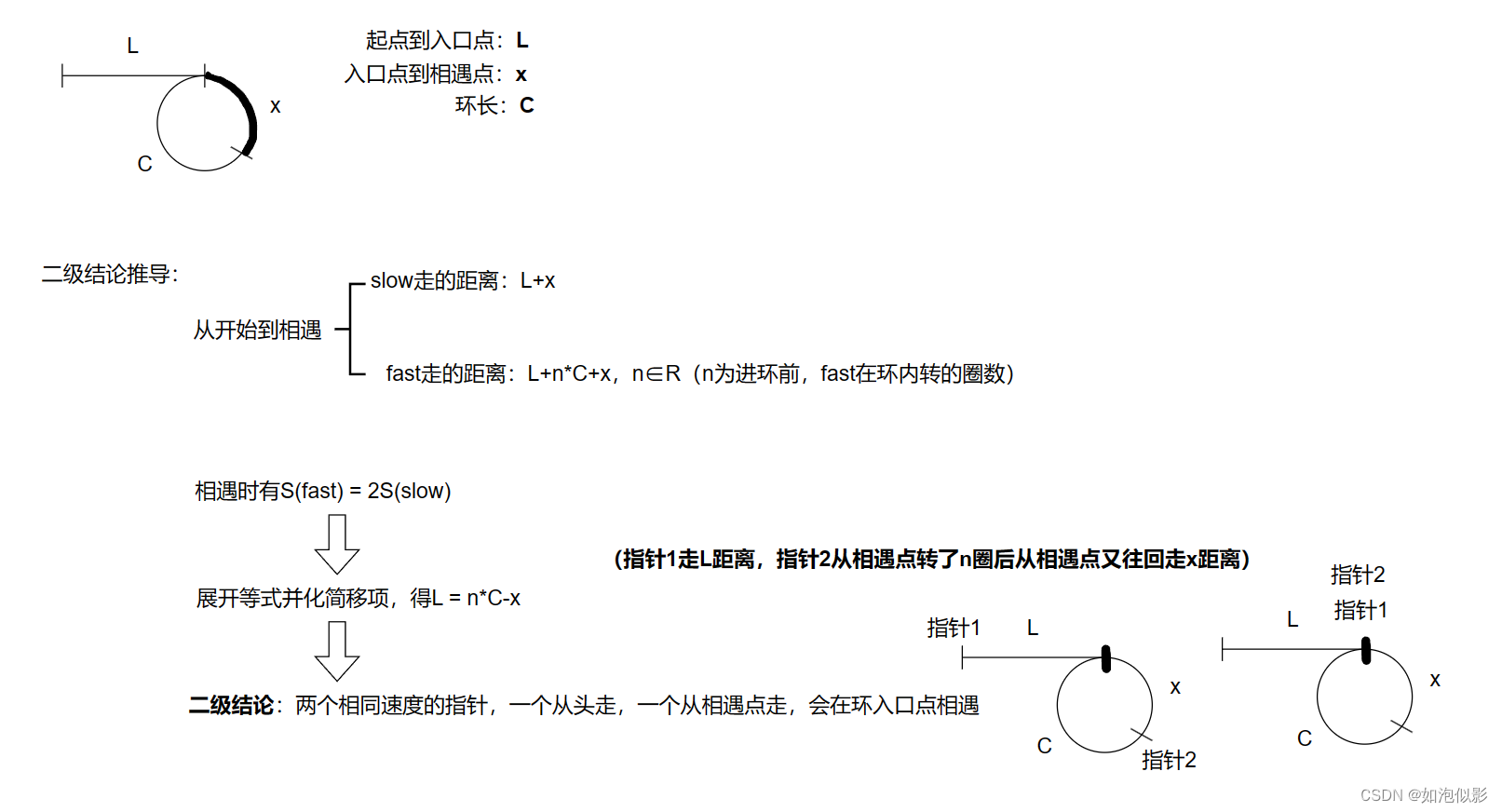
2. 找入口点（二级结论法）

二级结论：一个指针从相遇点，一个指针从头开始走，它们会在环的入口点相遇。

1. 设未知数，写出相遇时快慢指针走的图示距离
2. 展开两指针所走距离的理论关系式
3. 化简移项成 L = …的形式，推导出结论

• 代码实现

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;

    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        //走到相遇点
        if(fast == slow)
            {
               struct ListNode* meet = fast;
               struct ListNode* start = head;
               //走到相遇即入口点
               while(meet != start)
               {
                   meet = meet->next;
                   start = start->next;
               }
               return meet;
            }
    }
    return NULL;
}

  3. 拓展思考

1. slow一次走1步，fast一次走2步，一定会相遇吗？
2. slow一次走1步，fast一次走3步，一定会相遇吗？
3. slow一次走n步，fast一次走m步，一定会相遇吗？（m>n>1）

1. 一定会
   
2. “不一定”
   

这里思考一下结论3是否正确？

1. 让我们展开快慢指针的路程关系式S(fast) = 3S(slow)
   3L = L + n*C - N
   2L = n *C - N
2. 注意等式左边2L为偶数，
   右边n*C为偶数，N为奇数，偶-奇得奇
   那么等式两边的关系为偶数 = 奇数 ，这可能存在吗？答案是否定的，这里我们推导结论3不严谨，即不可能出现N为奇数，C为偶数这种情况。所以只存在两种情况，一定能追上

3. 不一定
   

1. 根据问题2，我们了解到路程关系式可以帮助我们判断结论是否合理
   展开路程关系式S(fast) =m/n * S(slow)
   m/n *L = L + n *C -N
   (m/n - 1)*L = n *C -N
2. 根据具体的m，n值带入即可，建议化成 fast = m/n slow 的形式，推导出结论后，根据路程关系式判断是否合理

---

总结

本文介绍了环形链表的概念并给出OJ题中常见设问的解答，最后扩展延伸了一下快慢指针在环形链表中的运用。希望能帮助读者理解并掌握环形链表的处理方法。如果对你有所帮助，还望点赞收藏支持博主。
文章中有什么不对的丶可改正的丶可优化的地方，欢迎各位来评论区指点交流，博主看到后会一一回复。